第361题
设函数\(f\left ( {x} \right )={e}^{2x}-a\mathrm{ln}x\) .
(I)讨论\(f\left ( {x} \right )\) 的导函数\(f'\left ( {x} \right )\)的零点的个数;
(II)证明:当\(a>0\)时\( \mathrm{f}\left(x\right)\ge 2a+a\mathrm{ln}\frac{2}{a}\).
参考答案:见解析
解析:
解:(I) \( f\left(x\right)\) 的定义域为 \(\left ( {0,+\infty } \right ){,f}^{\, '}\left ( {x} \right )=2{e}^{2x}-\frac {a} {x}(x>0)\) .
当 \( a\)≤0 时, \({f}^{\, '}\left ( {x} \right )>0,{f}^{\, '}\left ( {x} \right )\) 没有零点;
当 \( a>0\) 时,因为 \( {e}^{2x}\) 单调递增, \( -\frac{a}{x}\) 单调递减,所以 \({f}^{\, '}\left ( {x} \right )\) 在 \( \left(0,+\infty \right)\) 单调递增,又 \({f}^{\, '}\left ( {a} \right )>0\) ,当\(b\)满足 \(0<b<\frac {a} {4}\) 且 \(b<\frac {1} {4}\) 时, \({f}^{\, '}\left ( {b} \right )<0\) ,故当 \( a\)<0 时 \({f}^{\, '}\left ( {x} \right )\) 存在唯一零点.
(II)由(I),可设 \({f}^{\, '}\left ( {x} \right )\) 在 \( \left(0,+\infty \right)\) 的唯一零点为 \( {x}_{0}\) ,当 \( x\in \left(0,{x}_{0}\right)\) 时,\({f}^{\, '}\left ( {x} \right )<0\);
当 \( x\in \left({x}_{0},+\infty \right)\) 时, \({f}^{\, '}\left ( {x} \right )>0\),故 \( f\left(x\right)\) 在 \( \left(0,+\infty \right)\) 单调递减,在 \( \left({x}_{0},+\infty \right)\) 单调递增,所以 \( x={x}_{0}\) 时, \( f\left(x\right)\) 取得最小值,最小值为 \( f\left({x}_{0}\right)\) .
由于 \( 2{e}^{2{x}_{0}}-\frac{a}{{x}_{0}}=0\) ,所以 \( f\left({x}_{0}\right)=\frac{a}{2{x}_{0}}+2a{x}_{0}+a\mathrm{ln}\frac{2}{a}\ge 2a+a\mathrm{ln}\frac{2}{a}\) .
故当\(a>0\)时,\( f\left(x\right)\ge 2a+a\mathrm{ln}\frac{2}{a}\).
第362题
已知函数 \(g\left ( {x} \right )=λx+\mathrm{sin}x\) 是区间 \([ - 1\),\(1]\) 上的减函数.
(Ⅰ)若 \(g(x)⩽{t^2} + \lambda t + 1\) 在\(x \in [ - 1\),\(1]\)及\(\lambda \)所在的取值范围上恒成立,求\(t\)的取值范围;
(Ⅱ)试讨论函数\( \mathrm{h}\left(x\right)=\frac{\mathrm{ln}x}{f\left(x\right)}-{x}^{2}+2ex-m\)的零点的个数.
参考答案:见解析
解析:
(Ⅰ)由 \( g\text{'}\left(x\right)=\lambda +\mathrm{cos}x\)
又 \(\because g(x)\) 在 \([ - 1\),\(1]\) 上单调递减, \(\therefore g'(x)⩽0\) 在 \([ - 1\),\(1]\) 上恒成立.
\(\therefore \lambda ⩽ - \cos x\) 对 \(x \in [ - 1\),\(1]\) 恒成立,\( \because {[-\mathrm{cos}x]}_{min}=-1\) \(\therefore \lambda ⩽-1\)
\(\because g(x)⩽{t^2} + \lambda t + 1\) 在 \(x \in [ - 1\),\(1]\) 上恒成立,即 \(g{(x{)}_{\text{max}}}⩽{{t}^{2}}+\lambda t+1\)
\(\because g{(x)_{max}} = g( - 1) = - \lambda - \sin 1\) , \(\therefore - \lambda - \sin 1⩽{t^2} + \lambda t + 1\) ,即 \((t + 1)\lambda + {t^2} + \sin 1 + 1⩾0\) 对 \(\lambda ⩽ - 1\) 恒成立。
令 \(F(\lambda ) = (t + 1)\lambda + {t^2} + \sin 1 + 1(\lambda ⩽ - 1)\) ,则 \(\left \{ \begin{array}{*{20}{l}} {t+1⩽0} \\\ {-t-1+{{t}^{2}}+\sin {1}+1⩾0} \end{array} \right .\)
\(\therefore \) \(\left\{ {\begin{array}{*{20}{l}} {t⩽ - 1} \\\ {{t^2} - t + \sin 1⩾0} \end{array}} \right.\) , \(\therefore t⩽ - 1\)
(Ⅱ)讨论函数\( \mathrm{h}\left(x\right)=\frac{\mathrm{ln}x}{x}-{x}^{2}+2ex-m\)的零点的个数,即讨论方程 \( \frac{\mathrm{ln}x}{x}={x}^{2}-2ex+m\) 根的个数.令\( {f}_{1}\left(x\right)=\frac{\mathrm{ln}x}{x}\), \( {f}_{2}\left(x\right)={x}^{2}-2ex+m\),
\( \because {f}_{1}^{\text{'}}\left(x\right)=\frac{1-\mathrm{ln}x}{{x}^{2}}\),\(\therefore \)当\( \mathrm{x}\in \left(0,e\right)\)时, \({f_1}\prime (x) > 0\) ,\(\therefore {f_1}(x)\) 在\( \left(0,e\right)\)上为增函数;
当\( \mathrm{x}\in \left(e,+\mathrm{\infty }\right)\)时, \({f_1}\prime (x) < 0\) , \(\therefore {f_1}(x)\) 在\( \left(e,+\mathrm{\infty }\right)\)上为减函数,
\(\therefore \)当\( \mathrm{x}=\mathrm{e}\)时,\( {f}_{1}{\left(\mathrm{x}\right)}_{max}={f}_{1}\left(e\right)=\frac{1}{e}\) 而\( {f}_{2}\left(x\right)={\left(x-e\right)}^{2}+m-{e}^{2}\),
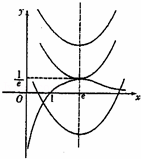
\(\therefore \)函数 \({f_1}(x)\) 、 \({f_2}(x)\) 在同一坐标系的大致图象如图所示,
\(\therefore \)①当\( \mathrm{m}-{e}^{2}>\frac{1}{e}\),即\( \mathrm{m}>{e}^{2}+\frac{1}{e}\)时,方程无解.函数 \(h(x)\) 没有零点;
②当\( \mathrm{m}-{e}^{2}=\frac{1}{e}\),即\( \mathrm{m}={e}^{2}+\frac{1}{e}\)时,方程有一个根.函数 \(h(x)\) 有1个零点
③当\( \mathrm{m}-{e}^{2}<\frac{1}{e}\),即\( \mathrm{m}<{e}^{2}+\frac{1}{e}\)时,方程有两个根.函数 \(h(x)\) 有2个零点
第364题
已知正四棱锥的侧棱长为 \(l\) ,其各顶点都在同一球面上.若该球的体积为 \(36\pi \) ,且 \(3 \leqslant l \leqslant 3\sqrt 3 \) ,则该正四棱锥体积的取值范围是( )
A.\([18,\frac{{81}}{4}]\)
B.\([\frac{{27}}{4},\frac{{81}}{4}]\)
C.\([\frac{{27}}{4},\frac{{64}}{3}]\)
D.\([18,64]\)
参考答案:C
第369题
定义:如果函数 \(f\left( x \right)\) 在 \(\left[ {a,b} \right]\) 上存在 \({x_1}\) , \({x_2}\) ( \(a < {x_1} < {x_2} < b\) ),满足 \(f'\left( {{x_1}} \right) = f'\left( {{x_2}} \right) = \frac{{f\left( a \right) - f\left( b \right)}}{{a - b}}\) ,则称 \({x_1}\) , \({x_2}\) 为 \(\left[ {a,b} \right]\) 上的“对望数”.已知函数 \(f\left( x \right)\) 为 \(\left[ {a,b} \right]\) 上的“对望函数”.下列结论正确的是( )
A.函数 \(f\left( x \right) = {x^2} + mx + n\) 在任意区间 \(\left[ {a,b} \right]\) 上都不可能是“对望函数”
B.函数 \(f\left( x \right) = \frac{1}{3}{x^3} - {x^2} + 2\) 是 \(\left[ {0,2} \right]\) 上的“对望函数”
C.函数\( \mathrm{f}\left(x\right)=x+\mathrm{sin}x\) 是 \(\left[ {\frac{\pi }{6},\frac{{11\pi }}{6}} \right]\) 上的“对望函数”
D.若函数 \(f\left( x \right)\) 为 \(\left[ {a,b} \right]\) 上的“对望函数”,则 \(f\left( x \right)\) 在 \(\left[ {a,b} \right]\) 上单调
参考答案:ABC
解析:
分析:根据“对望函数”的定义,代入具体函数依次判断,可判断A,B,C;若函数\(f\left( x \right)\)为\(\left[ {a,b} \right]\)上的“对望函数”,则\(f'\left( x \right) = 0\)在\(\left[ {a,b} \right]\)上必有两个不相等的实根,可判断D.
详解:对于A,因为\(f'\left( x \right) = 2x + m\)是单调递增函数,所以在\(\left[ {a,b} \right]\)上不可能存在\({x_1}\),\({x_2}\)(\(a < {x_1} < {x_2} < b\)),满足\(f'\left( {{x_1}} \right) = f'\left( {{x_2}} \right)\),所以函数\(f\left( x \right) = {x^2} + mx + n\)在任意区间\(\left[ {a,b} \right]\)上都不可能是“对望函数”,故A正确;
对于B,\(f'\left( x \right) = {x^2} - 2x\),\(\frac{{f\left( 0 \right) - f\left( 2 \right)}}{{0 - 2}} = \frac{{2 - \frac{2}{3}}}{{ - 2}} = - \frac{2}{3}\),令\(f'\left( x \right) = {x^2} - 2x = - \frac{2}{3}\),得\({x_1} = \frac{{3 - \sqrt 3 }}{3}\),\({x_2} = \frac{{3 + \sqrt 3 }}{3}\),且\(0 < {x_1} < {x_2} < 2\),所以函数\(f\left( x \right) = \frac{1}{3}{x^3} - {x^2} + 2\)是\(\left[ {0,2} \right]\)上的“对望函数”,故B正确;
对于C,\(f'\left( x \right) = 1 + \cos x\),\(\frac{{f\left( {\frac{\pi }{6}} \right) - f\left( {\frac{{11\pi }}{6}} \right)}}{{\frac{\pi }{6} - \frac{{11\pi }}{6}}} = 1 - \frac{3}{{5\pi }}\),令\(f'\left( x \right) = 1 + \cos x = 1 - \frac{3}{{5\pi }}\),得\(\cos x = - \frac{3}{{5\pi }}\),因此存在\({x_1},{x_2} \in \left[ {\frac{\pi }{6},\frac{{11\pi }}{6}} \right]\),使得\(f'\left( {{x_1}} \right) = f'\left( {{x_2}} \right) = 1 - \frac{3}{{5\pi }}\),所以函数\(f\left( x \right) = x + \sin x\)是\(\left[ {\frac{\pi }{6},\frac{{11\pi }}{6}} \right]\)上的“对望函数”,故C正确;
对于D,若函数\(f\left( x \right)\)为\(\left[ {a,b} \right]\)上的“对望函数”,则\(f'\left( x \right) = 0\)在\(\left[ {a,b} \right]\)上必有两个不相等的实根,则函数\(f\left( x \right)\)在\(\left[ {a,b} \right]\)上不单调,故D错误.
故选:ABC
第372题
某地拟规划种植一批芍药,为了美观,将种植区域(区域Ⅰ)设计成半径为\(1km\) 的扇形 \(EAF\) ,中心角 \(\angle EAF = \theta \left( {\frac{\pi }{4} < \theta < \frac{\pi }{2}} \right)\) .为方便观赏,增加收入,在种植区域外围规划观赏区(区域Ⅱ)和休闲区(区域Ⅲ),并将外围区域按如图所示的方案扩建成正方形 \(ABCD\) ,其中点 \(E\) , \(F\) 分别在边 \(BC\) 和 \(CD\) 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
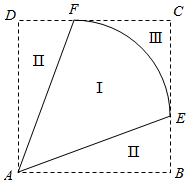
当 \(\theta \) 为多少时,年总收入最大?
参考答案:\(\frac{{\rm{\pi }}}{3}\)
种植区的面积为\({S}_{1}=\frac {1} {2}AF\cdot AE\cdot θ=\frac {1} {2}θ\),
正方形面积为 \(S = A{D^{\rm{2}}} = {\cos ^{\rm{2}}}\angle DAF = \frac{{1 + \cos 2\angle DAF}}{2} = \frac{{1 + \sin \theta }}{2}\) ,
设年总收入为 \(W(\theta )\) 万元,则
\(W(\theta ) = 10{S_Ⅰ} + 20{S_Ⅱ} + 20{S_Ⅲ} = 10{S_Ⅰ} + 20(S - {S_Ⅰ}) = 5\theta + 20\left( {\frac{{1 + \sin \theta }}{2} - \frac{1}{2}\theta } \right) = 10 + 10\sin \theta - 5\theta \) ,
其中 \(\frac{{\rm{\pi }}}{4} < \theta < \frac{{\rm{\pi }}}{2}\) ,求导可得 \(W'(\theta ) = 10\cos \theta - 5\) .
当 \(\frac{{\rm{\pi }}}{4} < \theta \leqslant \frac{{\rm{\pi }}}{3}\) 时, \(W'(\theta ) > 0\) , \(W(\theta )\) 递增;当 \(\frac{{\rm{\pi }}}{3} < \theta < \frac{{\rm{\pi }}}{2}\) 时, \(W'(\theta ) < 0\) , \(W(\theta )\) 递增.
所以当 \(\theta = \frac{{\pi }}{3}\) 时, \(W(\theta )\) 取得最大值,此时年总收入最大.
第373题
如图1所示为一种魔豆吊灯,图2为该吊灯的框架结构图,由正六棱锥\({O_1} - ABCDEF\) 和 \({O_2} - ABCDEF\) 构成,两个棱锥的侧棱长均相等,且棱锥底面外接圆的直径为\(1600\text{mm}\),底面中心为 \(O\) ,通过连接线及吸盘固定在天花板上,使棱锥的底面呈水平状态,下顶点 \({O_2}\) 与天花板的距离为\(1300\text{mm}\),所有的连接线都用特殊的金属条制成,设金属条的总长为 y .
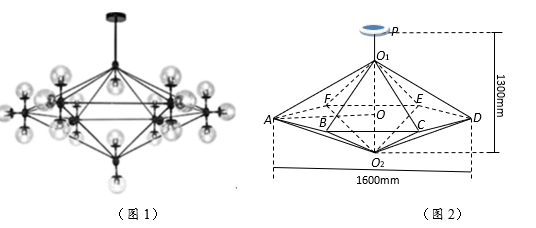
设\(∠{O}_{1}AO=\theta \left ( {\text{rad}} \right )\),当角\(θ\)正弦值的大小是多少时,金属条总长\(y\)最小.
参考答案:见解析
解析:
在直角三角形\(OA{O}_{1}\)中, \({O_1}A = \frac{{800}}{{\cos \theta }},O{O_1} = 800\tan \theta \) , \({O_1}P = 1300 - 1600\tan \theta \) ,
由 \(O{O_1} = 800\tan \theta > 0,{O_1}P = 1300 - 1600\tan \theta > 0\) ,所以 \(0 < \tan \theta < \frac{{13}}{{16}}\) ,
所以\(θ\)的范围是 \(0 < \theta < \alpha \) ,其中 \(\tan \alpha = \frac{{13}}{{16}}\) , \(\alpha \in (0,\frac{\pi }{2})\) .
从而有 \(y = 12{O_1}A + 6AB + {O_1}P\)\( = \frac{{12 \times 800}}{{\cos \theta }} + 6 \times 800 + 1300 - 1600\tan \theta \)
\( = \frac{{1600(6 - \sin \theta )}}{{\cos \theta }} + 6100\) ,
所以 \(y = \frac{{1600(6 - \sin \theta )}}{{\cos \theta }} + 6100\) , \(\theta \in (0,\alpha )\)(\(\tan \alpha = \frac{{13}}{{16}}\) , \(\alpha \in (0,\frac{\pi }{2})\)).
令 \(g(\theta ) = \frac{{6 - \sin \theta }}{{\cos \theta }}\) ,所以 \(g'(\theta ) = \frac{{6\sin \theta - 1}}{{{{\cos }^2}\theta }}\) ,
令 \(y' = 0\) ,则 \(\sin \theta = \frac{1}{6}\) ,则 \(\theta = {\theta _0}(tan{\theta _0} = \frac{1}{{\sqrt {35} }})\) .
当 \(\theta \in (0,{\theta _0})\) 时, \(y' < 0\) ;当 \(\theta \in ({\theta _0},\alpha )\) 时, \(y' > 0\) .
函数 \(g(\theta )\) 的单调性与 \(\theta \) 关系列表如下:
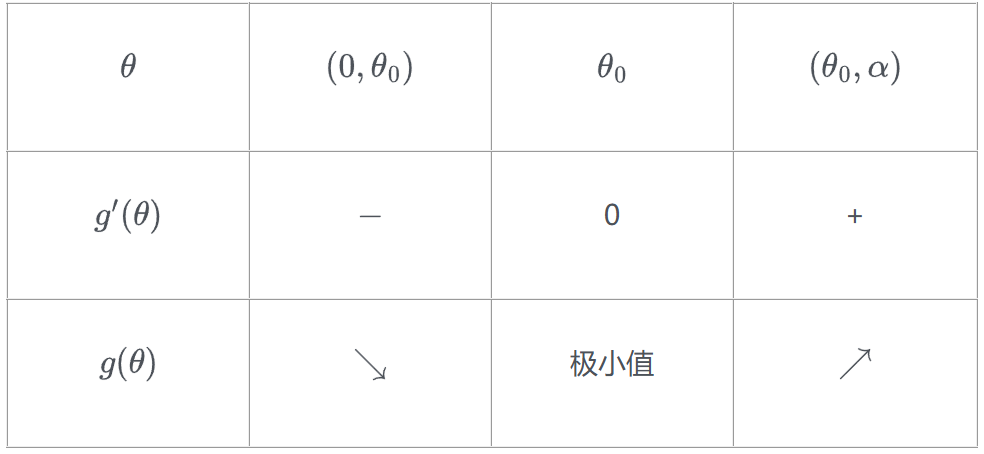
所以当 \(\theta = {\theta _0}\) ,其中 \(\tan {\theta _0} = \frac{{\sqrt {35} }}{{35}}\) 时 \(g(\theta )\) 取得最小值,即\(y\)最小.
故当角 \(\theta \) 满足 \(\sin \theta = \frac{1}{6}\) ( \(\tan \theta = \frac{{\sqrt {35} }}{{35}}\) )时,金属条总长\(y\)最小.
第374题
如图,已知\(A\),\(B\) 两镇分别位于东西湖岸\(MN\) 的\(A\) 处和湖中小岛的\(B\)处,点\(C\)在\(A\)的正西方向\(1\text{km}\)处,\( \mathrm{tan}\mathrm{\angle }BAN=\frac{3}{4}\),\(\angle BCN=\frac {\pi } {4}\) ,.现计划铺设一条电缆连通\(A,B\)两镇,有两种铺设方案:①沿线段\(AB\)在水下铺设;②在湖岸\(MN\)上选一点\(P\),先沿线段\(AP\)在地下铺设,再沿线段\(PB\) 在水下铺设,预算地下、水下的电缆铺设费用分别为2万元/km、4万元/km.
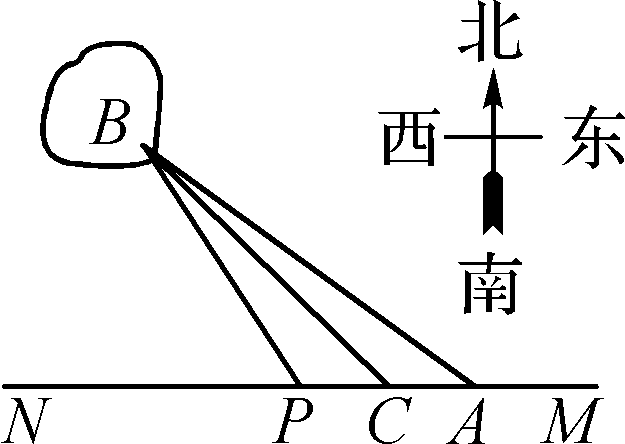
应该如何铺设,使总铺设费用最低?
参考答案:见解析
解析:
点\(P\) 选在\(A\)镇的正西方向\(\left ( {4-\sqrt {3}} \right )\text{km}\)处,总铺设费用最低
方案①:沿线段\(AB\)在水下铺设时,总铺设费用为5×4=20(万元)
方案②:设\(∠BPD=θ\),则 \(θ∈\left ( {{{\theta }_{o}},\frac {\pi } {2}} \right )\) ,其中 \({θ}_{0}=∠BAN\).
在\(Rt△BDP\)中, \(DP=\frac {BD} {\tan {\theta }}=\frac {3} {\tan {\theta }}\) , \(BP=\frac {BD} {\sin {\theta }}=\frac {3} {\sin {\theta }}\) ,
所以\(AP=4-DP=4-\frac {3} {\tan {\theta }}\) .
则总铺设费用为\(2AP+4BP=8-\frac {6} {\tan {\theta }}+\frac {12} {\sin {\theta }}=8+6\cdot \frac {2-\cos {\theta }} {\sin {\theta }}\)
设\(f(θ)=\frac {2-\cos {\theta }} {\sin {\theta }}\) ,则 \(f(θ)=\frac {{{\sin}^{2}}\theta -\left ( {2-\cos {\theta }} \right )\cos {\theta }} {{{\sin}^{2}}\theta }=\frac {1-2\cos {\theta }} {{{\sin}^{2}}\theta }\) ,
令\(f'(θ)=0\),得 \(\cos \theta = \frac{1}{2}\) 即 \(θ=\frac {\pi } {3}\) ,列表如下:
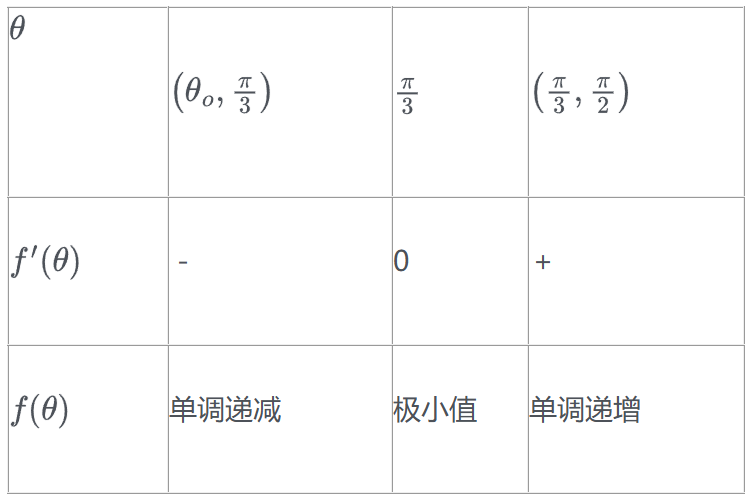
所以\(f(θ)\)的最小值为 \(f\left( {\frac{\pi }{3}} \right) = \sqrt 3 \) .
所以方案②的总铺设费用最低为 \(8 + 6\sqrt 3 \) (万元),此时 \(AP=4-\sqrt {3}\) .
而 \(8 + 6\sqrt 3 < 20\) ,所以应选择方案②进行铺设,点\(P\) 选在\(A\) 镇的正西方向\(\left ( {4-\sqrt {3}} \right )\text{km}\)处,总铺设费用最低.
第375题
某温泉度假村拟以泉眼\(C\)为圆心建造一个半径为 \(12\) 米的圆形温泉池,如图所示, \(M\) 、 \(N\) 是圆\(C\)上关于直径 \(AB\) 对称的两点,以 \(A\) 为圆心, \(AC\) 为半径的圆与圆  的弦 \(AM\) 、 \(AN\) 分别交于点\(D\) 、 \(E\) ,其中四边形 \(AEBD\) 为温泉区, I、II区域为池外休息区,III、IV区域为池内休息区,设 \(\angle MAB = \theta \) .
的弦 \(AM\) 、 \(AN\) 分别交于点\(D\) 、 \(E\) ,其中四边形 \(AEBD\) 为温泉区, I、II区域为池外休息区,III、IV区域为池内休息区,设 \(\angle MAB = \theta \) .
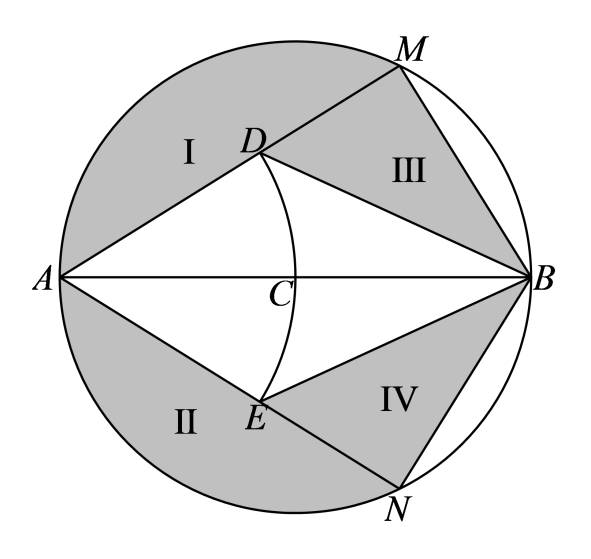
当池内休息区的总面积最大时,求 \(AM\) 的长.
参考答案:见解析
解析:
\(AM = (3 + 3\sqrt {33} )m\)
在 \(Rt\vartriangle ABM\) 中,因为\(AB=24\), \(\angle MAB = \theta \) ,
所以 \(BM = 24\sin \theta \) , \(AM = 24\cos \theta \) ,
\(MD = 24\cos \theta - 12\) ,由 \(BM = 24\sin \theta > 0\) , \(MD = 24\cos \theta - 12 > 0\) 得 \(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ,
则池内休息区总面积 \(S = 2 \cdot \frac{1}{2}MB \cdot DM = 24\sin \theta \left( {24\cos \theta - 12} \right) = 288\sin \theta \left( {2\cos \theta - 1} \right)\) ,\(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ;
设 \(f\left( \theta \right) = \sin \theta \left( {2\cos \theta - 1} \right)\) , \(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ,
因为 \(f'\left( \theta \right) = \cos \theta \left( {2\cos \theta - 1} \right) - 2{\sin ^2}\theta = 4{\cos ^2}\theta - \cos \theta - 2 = 0 \Rightarrow \cos \theta = \frac{{1 \pm \sqrt {33} }}{8}\) ,
又 \(\cos \theta = \frac{{1 + \sqrt {33} }}{8} > \frac{1}{2}\) ,所以 \(\exists {\theta _0} \in \left( {0,\frac{\pi }{3}} \right)\) ,使得 \(\cos {\theta _0} = \frac{{1 + \sqrt {33} }}{8}\) ,
则当 \(x \in \left( {0,{\theta _0}} \right)\) 时, \(f'\left( \theta \right) > 0 \Rightarrow f\left( \theta \right)\) 在 \(\left( {0,{\theta _0}} \right)\) 上单调增,
当 \(x \in \left( {{\theta _0},\frac{\pi }{3}} \right)\) 时, \(f'\left( \theta \right) < 0 \Rightarrow f\left( \theta \right)\) 在 \(\left( {0,{\theta _0}} \right)\) 上单调递减,
即 \(f\left( {{\theta _0}} \right)\) 是极大值,也是最大值,所以 \(f{\left( \theta \right)_{\max }} = f\left( {{\theta _0}} \right)\) ,此时\(AM = 24\cos {\theta _0} = 3 + 3\sqrt {33} \) .
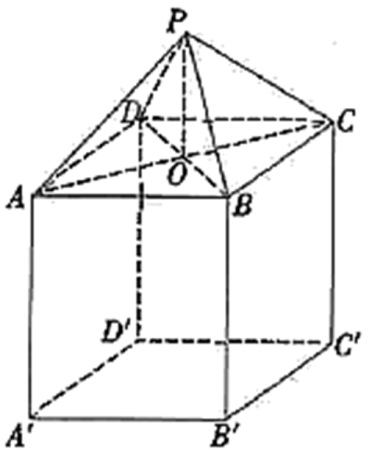
第376题
若三棱锥 \(P - ABC\) 是正四面体,求 \(x\) 的值;
参考答案:
\(x = \frac{{5\sqrt 3 }}{4}\left( {cm} \right)\)
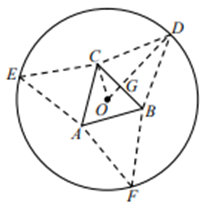
连结 \(OD\) ,交 \(BC\) 于点 \(G\) ,连结 \(OC\) ,
在 \(\vartriangle GOC\) 中, \(GC = x\) , \(GO = \frac{x}{{\sqrt 3 }}\) ,
则 \(GD = 5 - \frac{x}{{\sqrt 3 }}\) .
因为三棱锥 \(P - ABC\) 是正四面体,
所以 \(\vartriangle DBC\) 是正三角形,
所以 \(GD = \sqrt 3 GC\) ,即 \(5 - \frac{x}{{\sqrt 3 }} = \sqrt 3 x\) ,解得 \(x = \frac{{5\sqrt 3 }}{4}\left( {cm} \right)\) .
第377题
求三棱锥 \(P - ABC\) 的体积 \(V\) 的最大值,并指出相应 \(x\) 的值.
参考答案:见解析
解析:
最大值为\(4\sqrt {15} \left( {c{m^3}} \right)\),此时\(x = 2\sqrt 3 \left( {cm} \right)\).
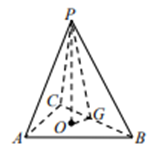
在 \(\vartriangle GOP\) 中, \(GO = \frac{x}{{\sqrt 3 }}\) , \(GP = 5 - \frac{x}{{\sqrt 3 }}\) ,
所以高 \(PO = \sqrt {G{P^2} - G{O^2}} = \sqrt {{{\left( {5 - \frac{x}{{\sqrt 3 }}} \right)}^2} - {{\left( {\frac{x}{{\sqrt 3 }}} \right)}^2}} = \sqrt {25 - \frac{{10x}}{{\sqrt 3 }}} \) .
由 \(25 - \frac{{10x}}{{\sqrt 3 }} > 0\) 可得, \(x < \frac{{5\sqrt 3 }}{2}\) .
所以三棱锥 \(P - ABC\) 的体积 \(V = \frac{1}{3}{S_{\vartriangle ABC}} \cdot PO = \frac{1}{3}\sqrt 3 {x^2} \cdot \sqrt {25 - \frac{{10x}}{{\sqrt 3 }}} \)
\( = \frac{{\sqrt {15} }}{3}\sqrt {5{x^4} - \frac{2}{{\sqrt 3 }}{x^5}} \) .
设函数 \(f\left( x \right) = 5{x^4} - \frac{2}{{\sqrt 3 }}{x^5}\) , \(0 < x < \frac{{5\sqrt 3 }}{2}\) ,
则 \({{f}^{'}}\left ( {x} \right )=20{{x}^{3}}-\frac {10} {\sqrt {3}}{{x}^{4}}=10{{x}^{3}}\left ( {2-\frac {x} {\sqrt {3}}} \right )\) .
令 \({{f}^{'}}\left ( {x} \right )=0\) 得, \(x = 2\sqrt 3 \) .列表如下:

所以 \(f\left( x \right)\) 在 \(x = 2\sqrt 3 \) 时取最大值 \(f\left( {2\sqrt 3 } \right) = 144\) ,
所以 \({V_{\max }} = 4\sqrt {15} \) .
所以 \({\left[ {f\left( x \right)} \right]_{\max }} = f\left( {2\sqrt 3 } \right) = 144\) ,所以 \({V_{\max }} = 4\sqrt {15} \) .
所以三棱锥 \(P - ABC\) 体积 \(V\) 的最大值为 \(4\sqrt {15} \left( {c{m^3}} \right)\) ,此时 \(x = 2\sqrt 3 \left( {cm} \right)\) .
第378题
若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让 \(CH + CP\) 最大,求该最大值;
参考答案:\(\frac{{2 + \sqrt 3 }}{4}\);
由题意,在 \(Rt\vartriangle ACB\) 中,可得 \(BC = 1 \times \cos \theta = \cos \theta \) ,
在 \(Rt\vartriangle CBH\) 中,可得 \(CH = \cos \theta \times \sin \theta = \sin \theta \cos \theta \) ,
在 \(Rt\vartriangle CBP\) 中,可得 \(CP = \cos \theta \sin \left( {\frac{\pi }{3} - \theta } \right)\) ,
所以 \(CH + CP = \sin \theta \cos \theta + \cos \theta \sin \left( {\frac{\pi }{3} - \theta } \right)\)\( = \sin \theta \cos \theta + \cos \theta \left( {\frac{{\sqrt 3 }}{2}\cos \theta - \frac{1}{2}\sin \theta } \right)\)
\( = \frac{1}{2}\sin \theta \cos \theta + \frac{{\sqrt 3 }}{2}{\cos ^2}\theta \)\( = \frac{1}{4}\sin 2\theta + \frac{{\sqrt 3 }}{2} \times \frac{{1 + \cos 2\theta }}{2}\)\( = \frac{1}{2}\sin \left( {2\theta + \frac{\pi }{3}} \right) + \frac{{\sqrt 3 }}{4}\) .
因为 \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,则 \(\frac{{4\pi }}{9} \leqslant 2\theta + \frac{\pi }{3} < \pi \) ,
所以当且仅当\(2\theta +\frac {\pi } {3}=\frac {\pi } {2}\),即 \(\theta = \frac{\pi }{{12}}\) 时, \(CH + CP\) 取得最大值,且最大值为 \(\frac{{2 + \sqrt 3 }}{4}\) 千米.
第379题
若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧\(CP\)和线段\(CH\) 的长度之和最大,求此时的 \(\theta \) 的值.
参考答案:见解析
解析:
\(\theta = \frac{\pi }{{18}}\)
取线段 \(BC\) 的中点 \(O\) ,连接 \(OP\) ,则 \(\angle COP = 2\angle CBP = 2\left( {\frac{\pi }{3} - \theta } \right) = \frac{{2\pi }}{3} - 2\theta \) .
由(1)知, \(CO = \frac{1}{2}BC = \frac{1}{2}\cos \theta \) , \(CH = \sin \theta \cos \theta \)
故\(\overset {\frown } {CP}\)的长为 \(\frac{1}{2}\cos \theta \cdot \left( {\frac{{2\pi }}{3} - 2\theta } \right) = \frac{\pi }{3}\cos \theta - \theta \cos \theta \) ,
则 \(\overset {\frown } {CP}\) 和线段 \(CH\) 的长度之和
\(y = \frac{\pi }{3}\cos \theta - \theta \cos \theta + \sin \theta \cos \theta \)\( = \cos \theta \left( {\frac{\pi }{3} - \theta + \sin \theta } \right)\) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) .
设 \(f\left( \theta \right) = \frac{\pi }{3} - \theta + \sin \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) , \(g\left( \theta \right) = \cos \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,
则 \(y = f\left( \theta \right)g\left( \theta \right)\) ,
因为 \(f'\left( \theta \right) = - 1 + \cos \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,所以 \(f'\left( \theta \right) = - 1 + \cos \theta < 0\) ,
故函数 \(f\left( \theta \right)\) 在区间 \(\left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) 上单调递减,故 \(f(\frac{{\sqrt 3 }}{2}) < f(\theta ) \leqslant f\left( {\frac{\pi }{{18}}} \right)\) .
易知函数 \(g\left( \theta \right)\) 在区间 \(\left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) 上也单调递减,所以 \(\frac{1}{2} < g\left( \theta \right) \leqslant g\left( {\frac{\pi }{{18}}} \right)\) ,
所以 \(f\left( \theta \right)g\left( \theta \right) \leqslant f\left( {\frac{\pi }{{18}}} \right) \cdot g\left( {\frac{\pi }{{18}}} \right)\) ,
所以当且仅当 \(\theta = \frac{\pi }{{18}}\) 时, \(\overset {\frown } {CP}\) 和线段 \(CH\) 的长度之和最大.
第380题
若 \(\mathop {\lim }\limits_{\Delta x \to + 0} \frac{{f({x_0} + \Delta x,{y_0}) - f({x_0},{y_0})}}{{\Delta x}}\) 存在,则称 \(\mathop {\lim }\limits_{\Delta x \to + 0} \frac{{f({x_0} + \Delta x,{y_0}) - f({x_0},{y_0})}}{{\Delta x}}\) 为二元函数 \(z = f\left( {x,y} \right)\) 在点 \(\left( {{x_0},{y_0}} \right)\) 处对 x 的偏导数,记为 \({f_x}\left( {{x_0},{y_0}} \right)\) ;若 \(\mathop {\lim }\limits_{\Delta y \to + 0} \frac{{f({x_0},{y_0} + \Delta y) - f({x_0},{y_0})}}{{\Delta y}}\) 存在,则称 \(\mathop {\lim }\limits_{\Delta y \to + 0} \frac{{f({x_0},{y_0} + \Delta y) - f({x_0},{y_0})}}{{\Delta y}}\) 为二元函数 \(z = f\left( {x,y} \right)\) 在点 \(\left( {{x_0},{y_0}} \right)\) 处对 y 的偏导数,记为 \({f_y}\left( {{x_0},{y_0}} \right)\) .
若二元函数 \(z = f\left( {x,y} \right) = {x^2} - 2xy + {y^3}\left( {x > 0,y > 0} \right)\) ,则下列结论正确的是( )
A.\({f_x}\left( {1,2} \right) = - 2\)
B.\({f_y}\left( {1,2} \right) = 10\)
C.\({f_x}\left( {m,n} \right) + {f_y}\left( {m,n} \right)\) 的最小值为 \( - 1\)
D.\(f\left( {x,y} \right)\) 的最小值为 \( - \frac{4}{{27}}\)
参考答案:ABD