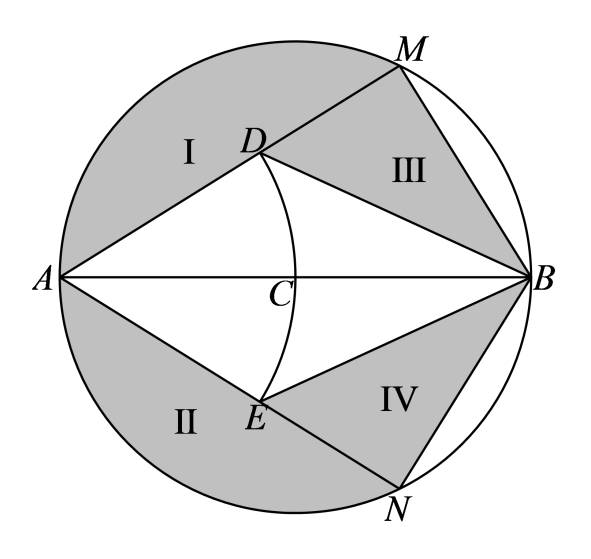
某温泉度假村拟以泉眼\(C\)为圆心建造一个半径为 \(12\) 米的圆形温泉池，如图所示， \(M\) 、 \(N\) 是圆\(C\)上关于直径 \(AB\) 对称的两点，以 \(A\) 为圆心， \(AC\) 为半径的圆与圆 
的弦 \(AM\) 、 \(AN\) 分别交于点\(D\) 、 \(E\) ，其中四边形 \(AEBD\) 为温泉区， I、II区域为池外休息区，III、IV区域为池内休息区，设 \(\angle MAB = \theta \) ．
当池内休息区的总面积最大时，求 \(AM\) 的长．
\(AM = (3 + 3\sqrt {33} )m\)
在 \(Rt\vartriangle ABM\) 中，因为\(AB=24\)， \(\angle MAB = \theta \) ，
所以 \(BM = 24\sin \theta \) ， \(AM = 24\cos \theta \) ，
\(MD = 24\cos \theta - 12\) ，由 \(BM = 24\sin \theta > 0\) ， \(MD = 24\cos \theta - 12 > 0\) 得 \(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ，
则池内休息区总面积 \(S = 2 \cdot \frac{1}{2}MB \cdot DM = 24\sin \theta \left( {24\cos \theta - 12} \right) = 288\sin \theta \left( {2\cos \theta - 1} \right)\) ，\(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ；
设 \(f\left( \theta \right) = \sin \theta \left( {2\cos \theta - 1} \right)\) ， \(\theta \in \left( {0,\frac{\pi }{3}} \right)\) ，
因为 \(f'\left( \theta \right) = \cos \theta \left( {2\cos \theta - 1} \right) - 2{\sin ^2}\theta = 4{\cos ^2}\theta - \cos \theta - 2 = 0 \Rightarrow \cos \theta = \frac{{1 \pm \sqrt {33} }}{8}\) ，
又 \(\cos \theta = \frac{{1 + \sqrt {33} }}{8} > \frac{1}{2}\) ，所以 \(\exists {\theta _0} \in \left( {0,\frac{\pi }{3}} \right)\) ，使得 \(\cos {\theta _0} = \frac{{1 + \sqrt {33} }}{8}\) ，
则当 \(x \in \left( {0,{\theta _0}} \right)\) 时， \(f'\left( \theta \right) > 0 \Rightarrow f\left( \theta \right)\) 在 \(\left( {0,{\theta _0}} \right)\) 上单调增，
当 \(x \in \left( {{\theta _0},\frac{\pi }{3}} \right)\) 时， \(f'\left( \theta \right) < 0 \Rightarrow f\left( \theta \right)\) 在 \(\left( {0,{\theta _0}} \right)\) 上单调递减，
即 \(f\left( {{\theta _0}} \right)\) 是极大值，也是最大值，所以 \(f{\left( \theta \right)_{\max }} = f\left( {{\theta _0}} \right)\) ，此时\(AM = 24\cos {\theta _0} = 3 + 3\sqrt {33} \) ．
