
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
如图,已知\(A\),\(B\) 两镇分别位于东西湖岸\(MN\) 的\(A\) 处和湖中小岛的\(B\)处,点\(C\)在\(A\)的正西方向\(1\text{km}\)处,\( \mathrm{tan}\mathrm{\angle }BAN=\frac{3}{4}\),\(\angle BCN=\frac {\pi } {4}\) ,.现计划铺设一条电缆连通\(A,B\)两镇,有两种铺设方案:①沿线段\(AB\)在水下铺设;②在湖岸\(MN\)上选一点\(P\),先沿线段\(AP\)在地下铺设,再沿线段\(PB\) 在水下铺设,预算地下、水下的电缆铺设费用分别为2万元/km、4万元/km.
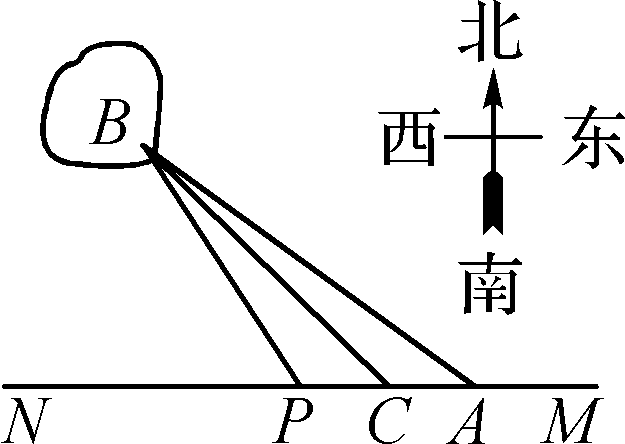
应该如何铺设,使总铺设费用最低?
知识点:第五章 一元函数的导数及其应用
参考答案:见解析
解析:
点\(P\) 选在\(A\)镇的正西方向\(\left ( {4-\sqrt {3}} \right )\text{km}\)处,总铺设费用最低
方案①:沿线段\(AB\)在水下铺设时,总铺设费用为5×4=20(万元)
方案②:设\(∠BPD=θ\),则 \(θ∈\left ( {{{\theta }_{o}},\frac {\pi } {2}} \right )\) ,其中 \({θ}_{0}=∠BAN\).
在\(Rt△BDP\)中, \(DP=\frac {BD} {\tan {\theta }}=\frac {3} {\tan {\theta }}\) , \(BP=\frac {BD} {\sin {\theta }}=\frac {3} {\sin {\theta }}\) ,
所以\(AP=4-DP=4-\frac {3} {\tan {\theta }}\) .
则总铺设费用为\(2AP+4BP=8-\frac {6} {\tan {\theta }}+\frac {12} {\sin {\theta }}=8+6\cdot \frac {2-\cos {\theta }} {\sin {\theta }}\)
设\(f(θ)=\frac {2-\cos {\theta }} {\sin {\theta }}\) ,则 \(f(θ)=\frac {{{\sin}^{2}}\theta -\left ( {2-\cos {\theta }} \right )\cos {\theta }} {{{\sin}^{2}}\theta }=\frac {1-2\cos {\theta }} {{{\sin}^{2}}\theta }\) ,
令\(f'(θ)=0\),得 \(\cos \theta = \frac{1}{2}\) 即 \(θ=\frac {\pi } {3}\) ,列表如下:
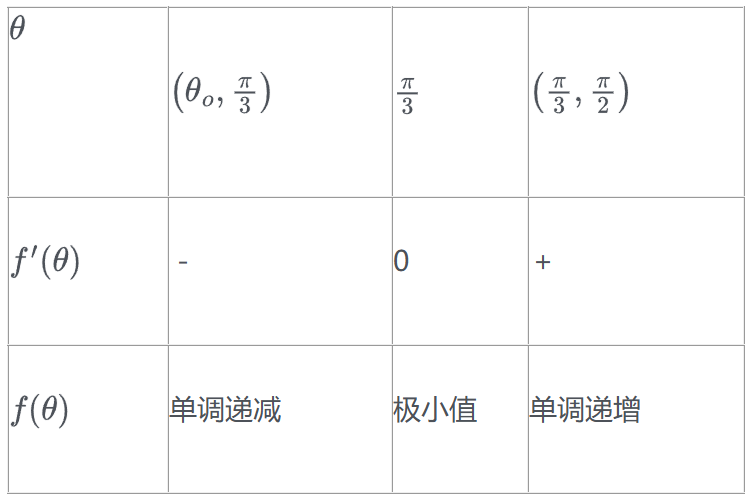
所以\(f(θ)\)的最小值为 \(f\left( {\frac{\pi }{3}} \right) = \sqrt 3 \) .
所以方案②的总铺设费用最低为 \(8 + 6\sqrt 3 \) (万元),此时 \(AP=4-\sqrt {3}\) .
而 \(8 + 6\sqrt 3 < 20\) ,所以应选择方案②进行铺设,点\(P\) 选在\(A\) 镇的正西方向\(\left ( {4-\sqrt {3}} \right )\text{km}\)处,总铺设费用最低.