
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
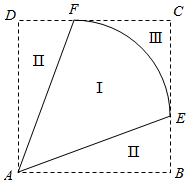
某地拟规划种植一批芍药,为了美观,将种植区域(区域Ⅰ)设计成半径为
当
知识点:第五章 一元函数的导数及其应用
参考答案:\(\frac{{\rm{\pi }}}{3}\)
种植区的面积为\({S}_{1}=\frac {1} {2}AF\cdot AE\cdot θ=\frac {1} {2}θ\),
正方形面积为 \(S = A{D^{\rm{2}}} = {\cos ^{\rm{2}}}\angle DAF = \frac{{1 + \cos 2\angle DAF}}{2} = \frac{{1 + \sin \theta }}{2}\) ,
设年总收入为 \(W(\theta )\) 万元,则
\(W(\theta ) = 10{S_Ⅰ} + 20{S_Ⅱ} + 20{S_Ⅲ} = 10{S_Ⅰ} + 20(S - {S_Ⅰ}) = 5\theta + 20\left( {\frac{{1 + \sin \theta }}{2} - \frac{1}{2}\theta } \right) = 10 + 10\sin \theta - 5\theta \) ,
其中 \(\frac{{\rm{\pi }}}{4} < \theta < \frac{{\rm{\pi }}}{2}\) ,求导可得 \(W'(\theta ) = 10\cos \theta - 5\) .
当 \(\frac{{\rm{\pi }}}{4} < \theta \leqslant \frac{{\rm{\pi }}}{3}\) 时, \(W'(\theta ) > 0\) , \(W(\theta )\) 递增;当 \(\frac{{\rm{\pi }}}{3} < \theta < \frac{{\rm{\pi }}}{2}\) 时, \(W'(\theta ) < 0\) , \(W(\theta )\) 递增.
所以当 \(\theta = \frac{{\pi }}{3}\) 时, \(W(\theta )\) 取得最大值,此时年总收入最大.