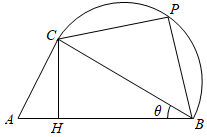
\(\theta = \frac{\pi }{{18}}\)
取线段 \(BC\) 的中点 \(O\) ,连接 \(OP\) ,则 \(\angle COP = 2\angle CBP = 2\left( {\frac{\pi }{3} - \theta } \right) = \frac{{2\pi }}{3} - 2\theta \) .
由(1)知, \(CO = \frac{1}{2}BC = \frac{1}{2}\cos \theta \) , \(CH = \sin \theta \cos \theta \)
故\(\overset {\frown } {CP}\)的长为 \(\frac{1}{2}\cos \theta \cdot \left( {\frac{{2\pi }}{3} - 2\theta } \right) = \frac{\pi }{3}\cos \theta - \theta \cos \theta \) ,
则 \(\overset {\frown } {CP}\) 和线段 \(CH\) 的长度之和
\(y = \frac{\pi }{3}\cos \theta - \theta \cos \theta + \sin \theta \cos \theta \)\( = \cos \theta \left( {\frac{\pi }{3} - \theta + \sin \theta } \right)\) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) .
设 \(f\left( \theta \right) = \frac{\pi }{3} - \theta + \sin \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) , \(g\left( \theta \right) = \cos \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,
则 \(y = f\left( \theta \right)g\left( \theta \right)\) ,
因为 \(f'\left( \theta \right) = - 1 + \cos \theta \) , \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,所以 \(f'\left( \theta \right) = - 1 + \cos \theta < 0\) ,
故函数 \(f\left( \theta \right)\) 在区间 \(\left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) 上单调递减,故 \(f(\frac{{\sqrt 3 }}{2}) < f(\theta ) \leqslant f\left( {\frac{\pi }{{18}}} \right)\) .
易知函数 \(g\left( \theta \right)\) 在区间 \(\left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) 上也单调递减,所以 \(\frac{1}{2} < g\left( \theta \right) \leqslant g\left( {\frac{\pi }{{18}}} \right)\) ,
所以 \(f\left( \theta \right)g\left( \theta \right) \leqslant f\left( {\frac{\pi }{{18}}} \right) \cdot g\left( {\frac{\pi }{{18}}} \right)\) ,
所以当且仅当 \(\theta = \frac{\pi }{{18}}\) 时, \(\overset {\frown } {CP}\) 和线段 \(CH\) 的长度之和最大.