第281题

A.\(\left ( {\frac {\pi } {4}，\pi } \right )\)

B.\(\left( { - \pi {\rm{,}} - \frac{\pi }{4}} \right) \cup \left( {\frac{\pi }{4}{\rm{,}}\pi } \right)\)

C.\(\left( { - \frac{\pi }{4}{\rm{,}}0} \right) \cup \left( {0{\rm{,}}\frac{\pi }{4}} \right)\)

D.\({\rm{ }}\left( { - \frac{\pi }{4}{\rm{,}}0} \right) \cup \left( {\frac{\pi }{4}{\rm{,}}\pi } \right)\)

参考答案：D

第282题

参考答案：①②④

第283题

参考答案：解：当 \(a = 0\) 时，函数 \(f\left( x \right) = x{\rm{sin}}x + {\rm{cos}}x,x \in \left[ {0{\rm{,}}\pi } \right]\) ，可得 \(f'\left( x \right) = {\rm{sin}}x + x{\rm{cos}}x - {\rm{sin}}x = x{\rm{cos}}x\).

当\(x\)在区间 \(\left[ {0{,}\pi } \right]\) 上变化时，\(f'\left( x \right)\)，\(f\left ( {x} \right )\)的变化如下表：

所以\(f\left( x \right)\)的单调增区间为 \(\left( {0{\rm{,}}\frac{\pi }{2}} \right)\) ；\(f\left( x \right)\)的单调减区间为 \(\left( {\frac{\pi }{2},\pi } \right)\) .

第284题

参考答案：（2）解：由题意，函数\(f\left( x \right) = x\sin x + \cos x + \frac{1}{2}a{x^2},x \in \left[ {0{\rm{,}}\pi } \right]\) ，可得 \(f'\left( x \right) = ax + x{\rm{cos}}x = x\left( {a + {\rm{cos}}x} \right)\)

当 \(a \geqslant 1\) 时，\(a + \cos x \geqslant 0\) 在 \([0,\pi ]\) 上恒成立，

所以 \(x \in [0,\pi ]\) 时，\(f'\left( x \right) \geqslant 0\) ，所以 \(f\left( x \right)\) 在 \([0,\pi ]\) 上单调递增.

又因为 \(f\left( 0 \right) = 1\) ，所以 f（x）在 \([0,\pi ]\) 上有0个零点.

当 \(0 < a < 1\) 时，令 \(f'\left( x \right) = 0\) ，可得 \({\rm{cos}}x = - a\).

由 \( - 1 < - a < 0\) 可知存在唯一的 \({x_0} \in \left( {\frac{\pi }{2}{\rm{,}}\pi } \right)\) 使得 \({\rm{cos}}{x_0} = - a\) ，

所以当 \(x \in [0,{x_0})\) 时， \(f'\left( x \right) \geqslant 0\) ， \(f\left( x \right)\) 单调递增；

当 \(x \in \left( {{x_0}{\rm{,}}\pi } \right)\) 时， \(f'\left( x \right) < 0\) ， \(f\left( x \right)\) 单调递减，

因为 \(f\left( 0 \right) = 1\) ，\(f\left ( {{x}_{0}} \right )>1\)，\(f\left( \pi \right) = \frac{1}{2}a{\pi ^2} - 1\) ，

①当 \(\frac{1}{2}a{\pi ^2} - 1 > 0\) ，即 \(\frac{2}{{{\pi ^2}}} < a < 1\) 时， \(f\left( x \right)\) 在 \([0,\pi ]\) 上有0个零点.

②当 \(\frac{1}{2}a{\pi ^2} - 1 \leqslant 0\) ，即 \(0 < a \leqslant \frac{2}{{{\pi ^2}}}\) 时，\(f\left( x \right)\) 在 \([0,\pi ]\) 上有1个零点.

综上可得：当 \(0 < a \leqslant \frac{2}{{{\pi ^2}}}\) 时，\(f\left( x \right)\) 有1个零点；

当 \(a > \frac{2}{{{\pi ^2}}}\) 时，\(f\left( x \right)\) 有0个零点.

第285题

A.\(f\left( {\tan \frac{{31{\rm{\pi }}}}{{24}}} \right) < f(2022) < f\left( {\ln \frac{1}{2}} \right)\)

B.\(f(2022) < f\left( {\tan \frac{{31{\rm{\pi }}}}{{24}}} \right) < f\left( {\ln \frac{1}{2}} \right)\)

C.\(f\left( {\ln \frac{1}{2}} \right) < f(2022) < f\left( {\tan \frac{{31{\rm{\pi }}}}{{24}}} \right)\)

D.\(f(2022) < f\left( {\ln \frac{1}{2}} \right) < f\left( {\tan \frac{{31{\rm{\pi }}}}{{24}}} \right)\)

参考答案：B

第286题

A.3

B.1

C.\( - 1\)

D.\( - 3\)

参考答案：D

第287题

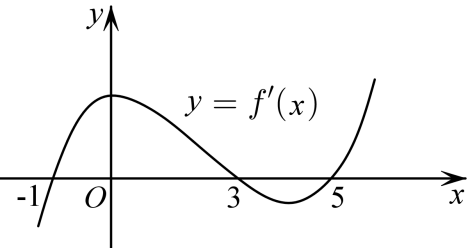
A.\(\left ( {-1，3} \right )\)为函数 \(y = f(x)\) 的单调递增区间

B.\(\left ( {0，5} \right )\)为函数 \(y = f(x)\) 的单调递减区间

C.函数 \(y = f(x)\) 在 \(x = 0\) 处取得极大值

D.函数 \(y = f(x)\) 在 \(x = 5\) 处取得极小值

参考答案：AD

第288题

A.\(h'\left( {{x_0}} \right) = 0\)，\({x_0}\) 是\(h\left( x \right)\)的极大值点

B.\(h'\left( {{x_0}} \right) = 0\)，\({x_0}\) 是\(h\left( x \right)\)的极小值点

C.\(h'\left( {{x_0}} \right) \ne 0\)，\({x_0}\) 不是\(h\left( x \right)\)的极大值点

D.\(h'\left( {{x_0}} \right) \ne 0\)，\({x_0}\) 是\(h\left( x \right)\)的极值点

参考答案：B

第289题

A.\(\exists \)\({{x}_{0}}\in \text{R}，f\left ( {{{x}_{0}}} \right )=0\)

B.函数 \(y = f\left( x \right)\) 的图象是中心对称图形

C.若\({x_0}\)是 \(f\left( x \right)\) 的极小值点，则\(f\left( x \right)\)在区间\(\left ( {-\infty {{，x}_{0}}} \right )\)单调递减

D.若\({x_0}\)是 \(f\left( x \right)\) 的极值点，则\(f'\left( {{x_0}} \right) = 0\)

参考答案：ABD

第290题

参考答案：\((0，\frac {2} {\pi })\)

第291题

参考答案：\(2a + b = - 3(a \ne - 3)\)

第292题

参考答案：\(0<a<\frac {1} {2}\)

第293题

参考答案：当 \(a = 1\) 时，\(f'\left( x \right) = 2\cos x - \frac{1}{x}\) ，则 \(f'\left( {\frac{{\rm{\pi }}}{2}} \right) = - \frac{2}{{\rm{\pi }}}\) ，所以曲线 \(y = f\left( x \right)\) 在点 \(\left( {\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{,2 - ln}}\frac{{\rm{\pi }}}{{\rm{2}}}} \right)\) 处的切线方程为:\(y - \left( {2 - \ln \frac{{\rm{\pi }}}{{\rm{2}}}} \right) = - \frac{{\rm{2}}}{{\rm{\pi }}}\left( {x - \frac{{\rm{\pi }}}{{\rm{2}}}} \right)\)，即 \(y = - \frac{2}{{\rm{\pi }}}x + 3 - \ln \frac{{\rm{\pi }}}{{\rm{2}}}\)．

第294题

参考答案：由题意得， \(f'\left( x \right) = 2\cos x - \frac{a}{x},(a > 0)\)，

因为函数 \(y = 2\cos x\)， \(y = - \frac{a}{x}\left( {a > 0} \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上均单调递增，

所以 \(f'\left( x \right) = 2\cos x - \frac{a}{x}\left( {a > 0} \right)\) 在区间 \(\left[ {{\rm{\pi }},2{\rm{\pi }}} \right)\) 上单调递增，

\(f'\left( {\rm{\pi }} \right) = - 2 - \frac{a}{{\rm{\pi }}} < 0\) ，

当 \(f'\left( {2{\rm{\pi }}} \right) = 2 - \frac{a}{{2{\rm{\pi }}}} > 0\) ，即 \(0 < a < 4{\rm{\pi }}\) 时，

\(f'\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上存在唯一的零点\(m\)，

则 \(f\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,}}m} \right)\) 上单调递减，在区间 \(\left( {m,2{\rm{\pi }}} \right)\) 上单调递增，

所以 \(f\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上只有1个极值点，且为极小值点，

当\(f'\left( {2{\rm{\pi }}} \right) = 2 - \frac{a}{{2{\rm{\pi }}}} \leqslant 0\) ，即 \(a \geqslant 4{\rm{\pi }}\) 时，\(f'\left( x \right) < 0\) 对 \(x \in \left[ {{\rm{\pi ,2\pi }}} \right)\)恒成立，

所以 \(f\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上单调递减，没有极值，即极值个数为0，

综合上述，当 \(0 < a < 4{\rm{\pi }}\) 时， \(f\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上极值点个数为1；

当 \(a \geqslant 4{\rm{\pi }}\) 时， \(f\left( x \right)\) 在区间 \(\left[ {{\rm{\pi ,2\pi }}} \right)\) 上极值点个数为0.

第295题

A.\(a{x^3} + bx + 1\)

B.\(ax - b\ln x\)

C.\(a\sin x + b\cos x + 1\)

D.\(a{x^2} + bx + 1\)

参考答案：BCD

第296题

A.当 \(0 < a < 1\) 时，函数 \(f\left( x \right)\) 没有极大值，有极小值

B.当 \(a > 1\) 时，函数\(f\left( x \right)\)既有极大值也有极小值

C.当 \(a = 1\) 时，函数\(f\left( x \right)\)有极大值，没有极小值

D.当\(a\le -{e}^{-2}\) 时，函数\(f\left( x \right)\)没有极值

参考答案：AD

第297题

参考答案：2

第298题

A.\(-1\)

B.0

C.1

D.2

参考答案：A

第299题

A.\(f\left ( {x} \right )\)在\(x=e\)处的切线方程为\(y=e\)

B.函数\(f\left ( {x} \right )\)的单调递减区间为\(\left ( {0，e} \right )\)

C.\(f\left ( {x} \right )\)的极小值为\(e\)

D.方程\(f\left ( {x} \right )=3\)有2个不同的解

参考答案：B

第300题

参考答案：\(\because f\left( x \right) = {x^2}\left( {x - 2} \right) = {x^3} - 2{x^2}\) ，所以， \(f'\left( x \right) = 3{x^2} - 4x\).

由 \(f'\left( x \right) = 3{x^2} - 4x > 0\)，解得 \(x < 0\) 或 \(x > \frac{4}{3}\)；

由 \(f'\left( x \right) = 3{x^2} - 2x < 0\)，解得 \(0 < x < \frac{4}{3}\) ，

所以\(f\left ( {x} \right )\)的递增区间为 \(\left( { - \infty ,0} \right)\) 、 \(\left( {\frac{4}{3}, + \infty } \right)\) ，递减区间为 \(\left( {0,\frac{4}{3}} \right)\).