“微信扫一扫”进入考试题库练习及模拟考试
高中数学选择性必修 第二册(381题)
第261题
下列求导过程正确的是( )
A.\( (\frac{1}{x}{)}^{\text{'}}=\frac{1}{{x}^{2}}\)
B.\( (\mathrm{cos}x{)}^{\text{'}}=\mathrm{sin}x\)
C.\( ({2}^{x}{)}^{\text{'}}={2}^{x}\mathrm{ln}2\)
D.\( ({\mathrm{log}}_{2}x{)}^{\text{'}}=\frac{1}{x}\mathrm{ln}2\)
参考答案:C
第262题
下列求导过程错误的是( )
A.\( ({x}^{-2}{)}^{\text{'}}=-2{x}^{-1}\)
B.\( (\mathrm{sin}x{)}^{\text{'}}=\mathrm{cos}x\)
C.\( ({3}^{x}{)}^{\text{'}}=x\cdot {3}^{x-1}\)
D.\( (x{)}^{\text{'}}=\frac{1}{x}\)
参考答案:ACD
第265题
下列结论中正确的是( )
A.若\( f\left(x\right)={x}^{4}\),则\({f}^{\, '}\left ( {2} \right )=32\)
B.若\( f\left(x\right)=\frac{1}{\sqrt{x}}\),则\({f}^{\, '}\left ( {2} \right )=-\frac {\sqrt {2}} {2}\)
C.若\( f\left(x\right)=\frac{1}{{x}^{2}\cdot \sqrt{x}}\),则\({f}^{\, '}\left ( {1} \right )=-\frac {5} {2}\)
D.若\( f\left(x\right)={x}^{-5}\),则\({f}^{\, '}(-1)=-5\)
参考答案:ACD
A.\( f\left(x\right)=\frac{1}{x}\)
B.\( f\left(x\right)={x}^{2}\)
C.\( f\left(x\right)={e}^{-x}\)
D.\( f\left(x\right)=\mathrm{ln}x\)
参考答案:ABD
A.\( \frac{3}{\mathrm{ln}3}\)
B.\( -\frac{3}{\mathrm{ln}3}\)
C.\( 3\mathrm{ln}3\)
D.\( -3\mathrm{ln}3\)
参考答案:C
第271题
若 \( f\left(x\right)\) 在 \((1,+\infty )\) 上不单调,求\(a\)的取值范围;
参考答案:\( f\text{'}\left(x\right)=\frac{a}{x}+2x=\frac{2{x}^{2}+a}{x}\left(x>0\right)\) .若 \( f\left(x\right)\) 在 \((1,+\infty )\) 上单调,则 \( f\text{'}\left(x\right)\ge 0\) 在 \((1,+\infty )\) 上恒成立,
所以 \( 2{x}^{2}+a\ge 0\) 在 \((1,+\infty )\) 上恒成立,所以 \( 2+a\ge 0\) ,即 \( a\ge -2\) .
因为 \( f\left(x\right)\) 在 \((1,+\infty )\) 上不单调,所以\(a\)的取值范围是 \((-\infty ,-2)\) .
第272题
若 \( f\left(x\right)\) 的最小值为 \( -2\) ,求\(a\).
参考答案:\( {f}^{\text{'}}\left(x\right)=\frac{a}{x}+2x=\frac{2{x}^{2}+a}{x}\left(x>0\right)\) .
①若 \( a\ge 0\) ,则 \( {f}^{\text{'}}\left(x\right)>0\) ,\( f\left(x\right)\) 在 \((0,+\infty )\) 上单调递增,此时 \( f\left(x\right)\) 无最值.
②若 \( a<0\),令 \( {f}^{\text{'}}\left(x\right)=0\) ,得 \(x = \pm \sqrt { - \frac{a}{2}} \).
当 \(x\in \left ( {0,\sqrt {-\frac {a} {2}}} \right )\) 时,\( f\text{'}\left(x\right)<0\);当 \(x\in \left ( {\sqrt {-\frac {a} {2}},+\infty } \right )\) 时,\( f\text{'}\left(x\right)>0\).
所以 \( f\left(x\right)\) 在 \(\left ( {0,\sqrt {-\frac {a} {2}}} \right )\) 上单调递减,在 \(\left ( {\sqrt {-\frac {a} {2}},+\infty } \right )\) 上单调递增.
所以 \( f\left(x\right)\) 的最小值是 \( f\left(\sqrt{-\frac{a}{2}}\right)=a\mathrm{ln}\sqrt{-\frac{a}{2}}-\frac{a}{2}-3=-2\) ,则 \( \frac{a}{2}\mathrm{ln}\left(-\frac{a}{2}\right)-\frac{a}{2}-1=0\).
令 \( g\left(x\right)=-x\mathrm{ln}x+x-1\),则 \( g\text{'}\left(x\right)=-x\mathrm{ln}x\),所以 \( g\left(x\right)\) 在 \(\left ( {0,1} \right )\) 上单调递增,在 \((1,+\infty )\) 上单调递减.
因为 \( g\left(1\right)=0\) ,所以方程 \( g\left(x\right)=0\) 只有一个根 \( x=1\) .由 \( -\frac{a}{2}=1\) ,得 \( a=-2\) ,即\(a\)的值为\(-2\)
参考答案:\( a\ge -4\)
第274题
已知函数 \( f\left(x\right)=x(\mathrm{ln}x{)}^{2}+x\) ,则( )
A.\( f\left(x\right)\) 在区间 \((0,+\infty )\) 上单调递增
B.当 \( x=\frac{1}{e}\) 时,\( f\left(x\right)\) 取最小值
C.对 \(\forall x\in \left ( {\frac {1} {e},+\infty } \right ),m>0,g\left ( {x} \right )=f\left ( {x+m} \right )-f\left ( {x} \right )\) 为增函数
D.对 \(\forall x\in \left ( {1,+\infty } \right )\) 都有 \( f\left(x\right)\le {x}^{3}\)
参考答案:ACD
A.\(\left ( {-1,1} \right )\)
B.\(\left . {[1,+\infty } \right )\)
C.\(\left ( {-1,+\infty } \right )\)
D.\(\left ( {-1,0} \right )\)
参考答案:B
A.
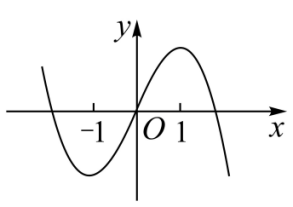
B.
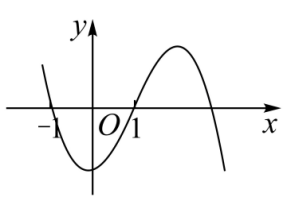
C.

D.
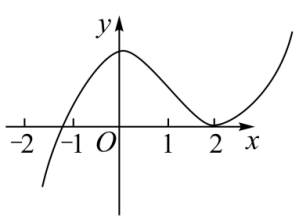
参考答案:C
第277题
“\( a\le -\frac{1}{2}\)”是“函数\( f\left(x\right)=x\left({e}^{x}-a\right)\)为增函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
参考答案:A
A.
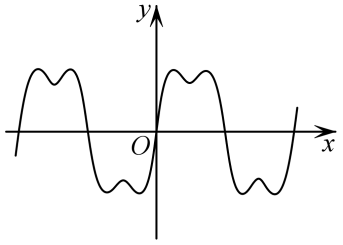
B.
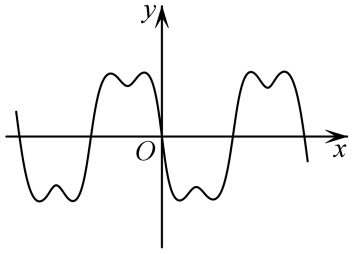
C.
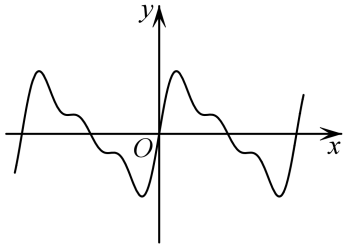
D.
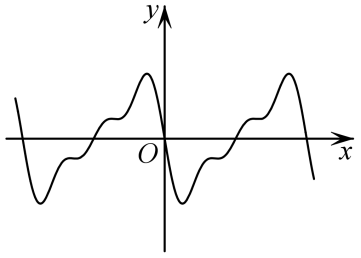
参考答案:C
解析:
点睛:有关函数图象识别问题的常见题型及解题思路(1)由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置;②由函数的单调性,判断图象的变化趋势;③由函数的奇偶性,判断图象的对称性;④由函数的周期性,判断图象的循环往复.
A.\(\left( { - \infty ,\frac{\pi }{2}} \right)\)
B.\(\left( {\frac{\pi }{2}, + \infty } \right)\)
C.\(\left( { - \infty ,\pi } \right)\)
D.\(\left( {\pi , + \infty } \right)\)
参考答案:A
A.函数 \(f\left( x \right)\) 在R上单调递增
B.函数 \(f\left( x \right)\) 在R上单调递增
C.函数 \(g\left( x \right)\) 的图象关于 \(\left( {1,0} \right)\) 中心对称
D.\({{\rm{e}}^{a - b}} > \frac{b}{a}\)
参考答案:AD