第201题

参考答案：解：\(\because {b_n} = \frac{4}{{{a_n} \cdot {a_{n + 1}}}} = \frac{4}{{\left( {4n - 2} \right)\left( {4n + 2} \right)}} = \frac{1}{{\left( {2n - 1} \right)\left( {2n + 1} \right)}} = \frac{1}{2}\left( {\frac{1}{{2n - 1}} - \frac{1}{{2n + 1}}} \right)\)，\(\therefore {S_n} = \frac{1}{2}\left[ {\left( {1 - \frac{1}{3}} \right) + \left( {\frac{1}{3} - \frac{1}{5}} \right) + \left( {\frac{1}{5} - \frac{1}{7}} \right) + \cdots + \left( {\frac{1}{{2n - 1}} - \frac{1}{{2n + 1}}} \right)} \right] = \frac{1}{2}\left( {1 - \frac{1}{{2n + 1}}} \right) = \frac{n}{{2n + 1}}\).

第202题

参考答案：解：设公比为\(q\)，∵\({a_1} = 1\)，\({a_3}{a_4} = \frac{1}{{32}}\)，∴\({q^5} = \frac{1}{{32}}\)，∴\(q = \frac{1}{2}\)，∴\({a_n} = {\left( {\frac{1}{2}} \right)^{n - 1}}\)；\({S_n} = \frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2 - {\left( {\frac{1}{2}} \right)^{n - 1}}\)

第203题

参考答案：解：∵\({b_n} = {\log _2}{a_n} = {\log _2}{\left( {\frac{1}{2}} \right)^{n - 1}} = 1 - n\)，∴\(\frac{1}{{{b_{n + 1}}{b_{n + 2}}}} = \frac{1}{{n(n + 1)}} = \frac{1}{n} - \frac{1}{{n + 1}}\)，∴\({T_{100}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \cdot \cdot \cdot + \frac{1}{{100}} - \frac{1}{{101}} = 1 - \frac{1}{{101}} = \frac{{100}}{{101}}\).

第204题

参考答案：解：当\(n=1\)时，\( 3{a}_{1}-2{S}_{1}={a}_{1}=2\)，

当 \(n\geq 2\) 时，由\( 2{S}_{n}=3{a}_{n}-2\)可得\( 2{S}_{n-1}=3{a}_{n-1}-2\)，

上述两个等式作差得 \( 2{a}_{n}=3{a}_{n}-3{a}_{n-1}\)，则\( {a}_{n}=3{a}_{n-1}\)，

所以，数列 \( \left\{{a}_{n}\right\}\) 是首项为\(2\)，公比为\(3\)的等比数列，故\( {a}_{n}=2\times {3}^{n-1}\).

设等差数列 \( \left\{{b}_{n}\right\}\) 的公差为\(d\)，则\(d≠0\)，因为 \({b}^{2}_{4}={b}_{2}\cdot {b}_{8}\)，即\( {\left(1+3d\right)}^{2}=\left(1+d\right)\left(1+7d\right)\)，

解得 \(d=1\)，因此，\( {b}_{n}={b}_{1}+\left(n-1\right)d=n\).

第205题

参考答案：解：由已知可得\( {c}_{n}=\left\{\begin{array}{c}2\times {3}^{n}，n为偶数\\ n+2，n为奇数\end{array}\right.\)，
所以，\( {T}_{2n}=\left(3+2\times {3}^{2}\right)+\left(5+2\times {3}^{4}\right)+\cdots +\left(2n+1+2\times {3}^{2n}\right)
=\left[3+5+\cdots +\left(2n+1\right)\right]+\left(2\times {3}^{2}+2\times {3}^{4}+\cdots +2\times {3}^{2n}\right)
=\frac{\left(3+2n+1\right)n}{2}+\frac{18\left(1-{9}^{n}\right)}{1-9}
={n}^{2}+2n+\frac{9\left({9}^{n}-1\right)}{4}\)

第206题

若函数\(f\left ( {x} \right )=\sqrt {x}\)在\(x={x}_{0}\)处的瞬时变化率是\(\frac {\sqrt {3}} {3}\)，则\({x}_{0}\)的值是（        ）

A.\(\frac {3} {4}\)

B.\(\frac {1} {2}\)

C.1

D.3

参考答案：A

第207题

A.\(\frac {1} {9}\)

B.\(\frac {5} {9}\)

C.\(\frac {13} {18}\)

D.\(\frac {17} {18}\)

参考答案：A

第208题

A.\(\sqrt {5}\)

B.2

C.3

D.1

参考答案：B

第209题

A.①②

B.②③

C.①④

D.③④

参考答案：B

第210题

A.前3s内球滚下的垂直距离的增量\(Δh=20\)m

B.在时间\(\left [ {2，3} \right ]\)内球滚下的垂直距离的增量\(Δh=12\)m

C.前3s内球在垂直方向上的平均速度为\(8{\text{m}/\text{s}}\)

D.在时间\(\left [ {2，3} \right ]\)内球在垂直方向上的平均速度为\(12{\text{m}/\text{s}}\)

参考答案：BCD

第211题

参考答案：0.1

解析：

第212题

参考答案：0.21

解析：

第213题

参考答案：2.1

解析：

第214题

参考答案：②④

第215题

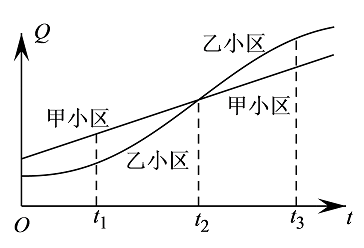
参考答案：\({k_1} > {k_2}\)

第216题

A.\(\frac {123} {6}\text{m}/\text{s}\)

B.\(\frac {125} {16}\text{m}/\text{s}\)

C.\(8\text{m}/\text{s}\)

D.\(\frac {67} {4}\text{m}/\text{s}\)

参考答案：B

第217题

A.1

B.\(\frac{5}{6}\)

C.\(\frac{1}{2}\)

D.\(\frac{1}{3}\)

参考答案：D

第218题

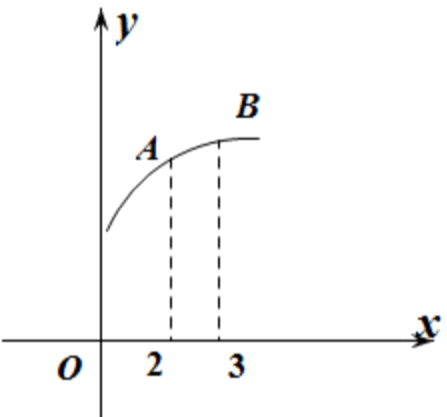
A.\(0 < f'(2) < f'(3) < f(3) - f(2)\)

B.\(0 < f'(3) < f(3) - f(2) < f'(2)\)

C.\(0<f\left ( {3} \right )-f\left ( {2} \right )<{f}^{\, '}\left ( {3} \right )<{f}^{\, '}\left ( {2} \right )\)

D.\(0 < f(3) - f(2) < {f^\prime }(2) < f(3)\)

参考答案：B

第219题

A.①②

B.①③④

C.②③

D.①③

参考答案：D

第220题

参考答案：\(\frac{1}{2}g\left( {2{t_0} + \Delta t} \right)\)

解析：