第161题

参考答案：\(\left( {{x_1} + {x_2} + {x_3}} \right)\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \frac{1}{{{x_3}}}} \right) = 3 + \left( {\frac{{{x_2}}}{{{x_1}}} + \frac{{{x_1}}}{{{x_2}}}} \right) + \left( {\frac{{{x_3}}}{{{x_1}}} + \frac{{{x_1}}}{{{x_3}}}} \right) + \left( {\frac{{{x_3}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_3}}}} \right) \geqslant 3 + 2 + 2 + 2 = 9\)

第162题

参考答案：猜想 \(\left( {{x_1} + {x_2} + \cdots + {x_n}} \right)\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_n}}}} \right) \geqslant {n^2}\,\left( {n \geqslant 2,\,n \in {N^*}} \right)\) ，
证明如下：①当 \(n = 2\) 时，由已知得猜想成立；
②假设当 \(n = k\) 时，猜想成立，即 \(\left( {{x_1} + {x_2} + \cdots + {x_k}} \right)\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_k}}}} \right) \geqslant {k^2}\) ， 则当 \(n = k + 1\) 时， \(\left( {{x_1} + {x_2} + \cdots + {x_k} + {x_{k + 1}}} \right)\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_k}}} + \frac{1}{{{x_{k + 1}}}}} \right)\) \( = \left( {{x_1} + {x_2} + \cdots + {x_k}} \right)\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_k}}}} \right) + \left( {{x_1} + {x_2} + \cdots + {x_k}} \right)\frac{1}{{{x_{k + 1}}}} + {x_{k + 1}}\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_k}}}} \right) + 1\) \( \geqslant {k^2} + \left( {{x_1} + {x_2} + \cdots + {x_k}} \right)\frac{1}{{{x_{k + 1}}}} + {x_{k + 1}}\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \cdots + \frac{1}{{{x_k}}}} \right) + 1\) \( = {k^2} + \left( {\frac{{{x_1}}}{{{x_{k + 1}}}} + \frac{{{x_{k + 1}}}}{{{x_1}}}} \right) + \left( {\frac{{{x_2}}}{{{x_{k + 1}}}} + \frac{{{x_{k + 1}}}}{{{x_2}}}} \right) + \cdots + \left( {\frac{{{x_2}}}{{{x_{k + 1}}}} + \frac{{{x_{k + 1}}}}{{{x_2}}}} \right) + 1\) ，\( \geqslant {k^2} + 2 + 2 + \cdots + 2 + 1 = {k^2} + 2k + 1 = {\left( {k + 1} \right)^2}\) 所以当 \(n = k + 1\) 时原式成立.
综合①②可知，猜想成立.

第163题

参考答案：猜想： \(n\) 个平面最多将空间分成\( {C}_{n}^{0}+{C}_{n}^{1}+{C}_{n}^{2}+{C}_{n}^{3}\)个部分( \(n > 2\) )；

第164题

参考答案：证明：设 \(n\) 个平面可将空间最多分成\(f(n)\)个部分，

当\(n=3\)时,3个平面可将空间分成８个部分，\( {C}_{3}^{0}+{C}_{3}^{1}+{C}_{3}^{2}+{C}_{3}^{3}=8\)，所以结论成立.

假设当n=k时，\( \mathrm{f}\left(k\right)={C}_{k}^{0}+{C}_{k}^{1}+{C}_{k}^{2}+{C}_{k}^{3}\)，则当\(n=k+1\)时，第 \(k + 1\) 个平面必与前面的 \(k\) 个平面产生\(k\)条交线，而由已知，这 \(k\) 条交线把第 \(k + 1\) 个平面最多分成 \( {C}_{k}^{0}+{C}_{k}^{1}+{C}_{k}^{2}\) 个部分，且每一部分将原有的空间分成两个部分，所以

\(f\left ( {k+1} \right )={f\left ( {k} \right )+C}^{0}_{k}+{C}^{1}_{k}+{C}^{2}_{k}=\left ( {{{C}^{0}_{k}+C}^{1}_{k}+{C}^{2}_{k}+{C}^{3}_{k}} \right )+\left ( {{{C}^{0}_{k}+C}^{1}_{k}+{C}^{2}_{k}} \right )\)　

\( {=C}_{k+1}^{0}+\left({{C}_{k}^{1}+C}_{k}^{0}\right)+\left({{C}_{k}^{2}+C}_{k}^{1}\right)+\left({{C}_{k}^{3}+C}_{k}^{2}\right){=C}_{k+1}^{0}+{C}_{k+1}^{1}+{C}_{k+1}^{2}+{C}_{k+1}^{3}\)

因此，当\(n=k+1\)时，结论成立.由数学归纳法原理可知，对 \(n \in {N^*}\) 且 \(n > 2\) ，得证.

第165题

A.回归直线 \(\hat y = \hat bx + \hat a\)至少经过点 \(\left( {{x_1},{y_1}} \right)\) ， \(\left( {{x_2},{y_2}} \right)\) ，…， \(\left( {{x_n},{y_n}} \right)\) 中的一个点

B.若 \(\overline x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} \) ， \(\overline y = \frac{1}{n}\sum\limits_{i = 1}^n {{y_1}} \) ，则回归直线 \(\hat y = \hat bx + \hat a\) 定经过点 \(\left( {\bar x,\bar y} \right)\)

C.若点 \(\left( {{x_1},{y_1}} \right)\) ， \(\left( {{x_2},{y_2}} \right)\) ，…， \(\left( {{x_n},{y_n}} \right)\) 都在直线 \(x - y + 2 = 0\) 上，则变量 \(x\) ， \(y\) 的相关系数 \(r = 1\)

D.若变量 \(x\) 增加一个单位时，则变量 \(y\) 平均增加或减少 \(\left| {\hat b} \right|\) 个单位

参考答案：BCD

第166题

A.\(-2.45\)

B.\(2.45\)

C.\(3.45\)

D.\(54.55\)

参考答案：B

第167题

A.\( \widehat{y}=3.2x-24\)

B.\( \widehat{y}=-3.2x+40\)

C.\( \widehat{y}=3x-24\)

D.\( \widehat{y}=-3x+40\)

参考答案：B

第168题

A.\(-0.96\)

B.\(-0.8\)

C.0.8

D.0.96

参考答案：C

第169题

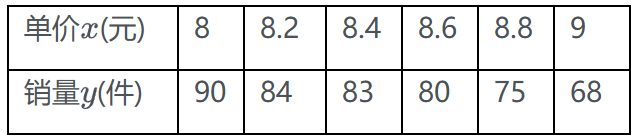
A.相关变量 \(x\) ， \(y\) 具有正相关关系

B.去除两个歧义点后的回归直线方程为 \(\widehat y = 3x - 3\)

C.去除两个歧义点后，样本 \(\left( {4,8.9} \right)\) 的残差为 \( - 0.1\)

D.去除两个歧义点后，随 \(x\) 值增加相关变量 \(y\) 值增加速度变小

参考答案：ABC

第170题

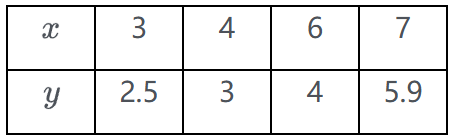
A.\(y\) 与 \(x\) 的相关系数 \(r < 0\)

B.产量为8吨时预测所需材料约为5.95吨

C.\(a = 0.35\)

D.产品产量增加1吨时，所需材料一定增加0.7吨

参考答案：BC

第171题

参考答案：\(\frac{1}{3}\)

第172题

参考答案：\(\hat y\)＝\(\frac{5}{2}\)\(x\)\( - 3\)

解：因为 \(\overline x = \frac{1}{3}\left( {11 + 13 + 12} \right) = 12,\overline y = \frac{1}{3}\left( {25 + 30 + 26} \right) = 27\)

所以 \(\sum\limits_{i = 1}^3 {({x_i} - \overline x )({y_i} - \overline y )} = 5,\sum\limits_{i = 1}^3 {{{({x_i} - \overline x )}^2}} = 2\)

则 \(\hat b = \frac{{\sum\limits_{i = 1}^3 {({x_i} - \overline x )({y_i} - \overline y )} }}{{\sum\limits_{i = 1}^3 {{{({x_i} - \overline x )}^2}} }} = \frac{5}{2}\)，\(\hat a = \overline y - \hat b\overline x = - 3\)

所以回归直线方程为 \(\hat{y}=\frac {5} {2}x-3\)

第173题

参考答案：可靠当 \(x = 10\) 时，\(\widehat y = \frac{5}{2} \times 10 - 3 = 22\)，\(\left| {22 - 23} \right| < 2\)当 \(x = 8\) 时，\(\widehat y = \frac{5}{2} \times 8 - 3 = 17\)，\(\left| {17 - 16} \right| < 2\)数据的误差均不超过2颗，所以得到的线性回归方程是可靠的.

第174题

参考答案：\(32\% \)当 \(x = 14\) 时，\(\widehat y = \frac{5}{2} \times 14 - 3 = 32\)所以温差为14℃的发芽率是 \(32\% \).

第175题

A.\(\frac{{2017}}{2}\)

B.\(1009\)

C.\(\frac{{2019}}{2}\)

D.\(1010\)

参考答案：B

解析：

第176题

A.\(2\left( {n - 1} \right)\)

B.\(2n\)

C.\({2^{n - 1}}\)

D.\({2^n}\)

参考答案：D

解析：

第177题

A.\( - 4044\)

B.\( - 2022\)

C.2022

D.4044

参考答案：A

解析：

第178题

参考答案：\(\frac{5}{{32}}\)

解析：

第179题

A.\({S_n} = {n^2} - 3n\)

B.\({S_n} = \frac{{3{n^2} - 9n}}{2}\)

C.\({a_n} = 3n - 6\)

D.\({{a}_{n}}=2n\)

参考答案：BC

解析：

第180题

参考答案：\(\frac{{19}}{2}\)

解析：