第121题

参考答案：2

解析：

第122题

参考答案：\( \frac{n(n+1)}{2}\)

解析：

第123题

参考答案：\( \frac{64}{7}(1-{2}^{-3n})\)

解析：

第124题

参考答案：设等差数列 \( \left\{{a}_{n}\right\}\) 的公差为 \( d\) ，因为 \( {a}_{2}={a}_{1}+d=6\) ， \( {S}_{5}=5{a}_{1}+\frac{5\times 4}{2}d=45\) ，所以 \( \left\{\begin{array}{c}{a}_{1}+d=6\\ {a}_{1}+2d=9\end{array}\right.\) ，解得 \( {a}_{1}=3,d=3\) ，所以 \( {a}_{n}=3+3\left(n-1\right)=3n\) ；

第125题

参考答案：由（1）可得， \( {b}_{n}={a}_{{2}^{n}}=3\times {2}^{n}\) ，

所以数列 \( \left\{{b}_{n}\right\}\) 的前\(n\)项和 \( {T}_{n}=\frac{3\times 2\left(1-{2}^{n}\right)}{1-2}=3\times {2}^{n+1}-6\) .

第126题

参考答案：由 \( \left\{\begin{array}{c}{S}_{2}=6{a}_{2}-42\left(1\right)\\ {S}_{3}={a}_{4}-42\left(2\right)\end{array}\right.\) ，-（1）得 \( {a}_{3}={a}_{4}-6{a}_{2}\) ，

即 \( {q}^{2}-q-6=0\) ，又 \( q>0\) ，∴ \( q=3\) .把 \( q=3\) 代入（1）得 \( {a}_{1}=3\) ，∴ \({a_n} = {3^n}\) ，

又∵ \( \frac{{b}_{1}}{{a}_{1}}+\frac{{b}_{2}}{{a}_{2}}+\cdots +\frac{{b}_{n}}{{a}_{n}}=1-\frac{n+1}{{3}^{n}}\left(n\in {N}^{*}\right)\) ，当 \( n=1\) 时， \( \frac{{b}_{1}}{{a}_{1}}=\frac{1}{3}\) ，

当 \( n\ge 2\) 时， \( \frac{{b}_{n}}{{a}_{n}}=1-\frac{n+1}{{3}^{n}}-\left(1-\frac{n}{{3}^{n-1}}\right)=\frac{2n-1}{{3}^{n}}\) ，因 \( n=1\) 时， \( \frac{{b}_{1}}{{a}_{1}}=\frac{1}{3}\) 也符合上式，

∴ \( \frac{{b}_{n}}{{a}_{n}}=\frac{2n-1}{{3}^{n}}\left(n\in {N}^{*}\right)\) ，又 \({a_n} = {3^n}\) ，∴ \( {b}_{n}=2n-1\left(n\in {N}^{*}\right)\) .

解析：

第127题

参考答案：由（1）知 \( {c}_{n}=\frac{1}{{a}_{{b}_{n}}}=\frac{1}{{3}^{2n-1}}\) ，

∴ \( {T}_{n}={c}_{1}+{c}_{2}+{c}_{3}+\cdots +{c}_{n}=\frac{1}{{3}^{1}}+\frac{1}{{3}^{3}}+\frac{1}{{3}^{5}}+\cdots +\frac{1}{{3}^{2n-1}}\) \( =\frac{\frac{1}{3}\left(1-\frac{1}{{9}^{n}}\right)}{1-\frac{1}{9}}=\frac{3}{8}\left(1-\frac{1}{{9}^{n}}\right)\) .

解析：

第128题

A.用样本相关系数r来刻画成对样本数据的相关程度时，若 \(\left| r \right|\) 越大，则成对样本数据的线性相关程度越强

B.经验回归方程 \(\widehat y = \widehat bx + \widehat a\) 一定经过点 \(\left( {\overline x ,\overline y } \right)\)

C.用残差平方和来刻画模型的拟合效果时，若残差平方和越小，则相应模型的拟合效果越好

D.用决定系数\({R^2}\)来刻画模型的拟合效果时，若 \({R^2}\) 越小，则相应模型的拟合效果越好

参考答案：D

第129题

A.\(0.5\)

B.\({e^{0.5}}\)

C.2

D.\({e^2}\)

参考答案：B

第130题

A.\(y=a+bx\)

B.\(y = a + b{x^2}\)

C.\(y = a + b{{\rm{e}}^x}\)

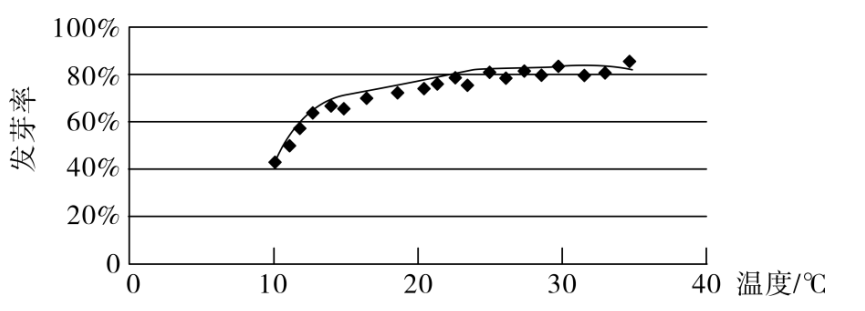
D.\(y = a + b\ln x\)

参考答案：D

第131题

A.①②④

B.②③④

C.①③④

D.②④

参考答案：B

第132题

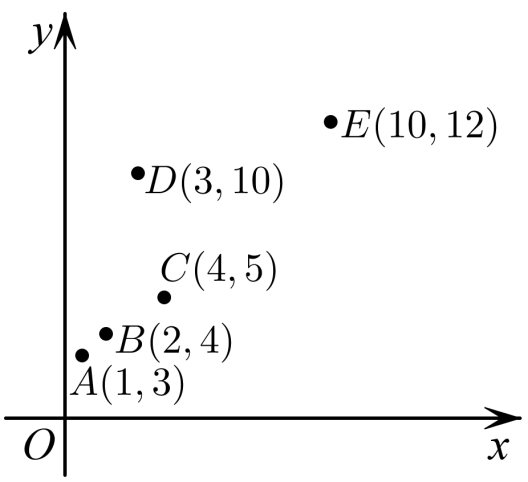
A.相关系数 \(r\) 变大

B.残差平方和变大

C.变量 \(x\) 与变量 \(y\)呈正相关

D.变量 \(x\) 与变量 \(y\) 的相关性变强

参考答案：ACD

第133题

A.两条回归直线的交点为 \(\left( {3.5,2.5} \right)\)

B.\(\hat{{a}_{1}}>\hat{{a}_{2}}\)

C.\(\hat{{b}_{1}}>\hat{{b}_{2}}\)

D.\({r_1} > {r_2}\)

参考答案：ACD

第134题

A.对于独立性检验，随机变量 \({\chi ^2}\) 的观测值值越小，判定“两变量有关系”犯错误的概率越小

B.在回归分析中，决定系数\({R^2}\)越大，说明回归模型拟合的效果越好

C.随机变量 \(\xi \sim B\left ( {n,p} \right )\)，若 \(E\left( x \right) = 30\)，\(D\left( x \right) = 20\)，则 \(n = 45\)

D.以 \(\widehat y = c{e^{kx}}\) 拟合一组数据时，经 \(z = \ln y\) 代换后的线性回归方程为 \(\widehat z = 0.3x + 4\)，则 \(c = {e^4}\)，\(k = 0.3\)

参考答案：BD

第135题

参考答案：4，5.0； 根据表格数据直接求解即可

第136题

参考答案：根据题意，结合参考数据和相关系数\(r\)的计算公式，求出\(r\)，即可判断\(x\)与\(y\)之间是否具有线性相关关系。

(I)\(\overline x = \frac{{2 + 3 + 4 + 5 + 6}}{5} = 4\)

\(\overline y = \frac{{2.2 + 3.8 + 5.5 + 6.5 + 7.0}}{5} = 5.0\)

(II)\(\sum\limits_{i = 1}^5 {{x_i}{y_i}} - 5\overline x \overline y = 112.3 - 5 \times 4 \times 5 = 12.3\)

\(\sum\limits_{i = 1}^5 {x_i^2} - 5{\overline x ^2} = 90 - 5 \times {4^2} = 10\)

\(\sum\limits_{i = 1}^5 {y_i^2} - 5{\overline y ^2} = 140.8 - 5 \times {5^2} = 15.8\)

所以\(r = \frac{{\sum\limits_{i = 1}^5 {{x_i}{y_i} - 5\overline x \overline y } }}{{\sqrt {\sum\limits_{i = 1}^5 {x_i^2 - 5{{\overline x }^2}} } \sqrt {\sum\limits_{i = 1}^5 {y_i^2 - 5{{\overline y }^2}} } }} = \frac{{12.3}}{{\sqrt {10 \times 15.8} }} \approx 0.987\)

所以有把握认为\(x\)与\(y\)之间具有线性相关关系，去求回归直线方程是有意义的。

第137题

参考答案：25

第138题

参考答案：①③

第139题

A.\(2k + 1\)

B.\(\left( {2k + 1} \right)\left( {2k + 2} \right)\)

C.\(\frac{{\left( {2k + 1} \right)\left( {2k + 2} \right)}}{{k + 1}}\)

D.\(\frac{{2k + 2}}{{k + 1}}\)

参考答案：C

解析：

第140题

参考答案：\({2^k}\)

解析：