
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
如图,要利用一半径为
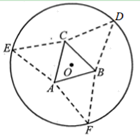
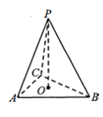
求三棱锥 \(P - ABC\) 的体积 \(V\) 的最大值,并指出相应 \(x\) 的值.
知识点:第五章 一元函数的导数及其应用
参考答案:见解析
解析:
最大值为\(4\sqrt {15} \left( {c{m^3}} \right)\),此时\(x = 2\sqrt 3 \left( {cm} \right)\).
在 \(\vartriangle GOP\) 中, \(GO = \frac{x}{{\sqrt 3 }}\) , \(GP = 5 - \frac{x}{{\sqrt 3 }}\) ,
所以高 \(PO = \sqrt {G{P^2} - G{O^2}} = \sqrt {{{\left( {5 - \frac{x}{{\sqrt 3 }}} \right)}^2} - {{\left( {\frac{x}{{\sqrt 3 }}} \right)}^2}} = \sqrt {25 - \frac{{10x}}{{\sqrt 3 }}} \) .
由 \(25 - \frac{{10x}}{{\sqrt 3 }} > 0\) 可得, \(x < \frac{{5\sqrt 3 }}{2}\) .
所以三棱锥 \(P - ABC\) 的体积 \(V = \frac{1}{3}{S_{\vartriangle ABC}} \cdot PO = \frac{1}{3}\sqrt 3 {x^2} \cdot \sqrt {25 - \frac{{10x}}{{\sqrt 3 }}} \)
\( = \frac{{\sqrt {15} }}{3}\sqrt {5{x^4} - \frac{2}{{\sqrt 3 }}{x^5}} \) .
设函数 \(f\left( x \right) = 5{x^4} - \frac{2}{{\sqrt 3 }}{x^5}\) , \(0 < x < \frac{{5\sqrt 3 }}{2}\) ,
则 \({{f}^{'}}\left ( {x} \right )=20{{x}^{3}}-\frac {10} {\sqrt {3}}{{x}^{4}}=10{{x}^{3}}\left ( {2-\frac {x} {\sqrt {3}}} \right )\) .
令 \({{f}^{'}}\left ( {x} \right )=0\) 得, \(x = 2\sqrt 3 \) .列表如下:

所以 \(f\left( x \right)\) 在 \(x = 2\sqrt 3 \) 时取最大值 \(f\left( {2\sqrt 3 } \right) = 144\) ,
所以 \({V_{\max }} = 4\sqrt {15} \) .
所以 \({\left[ {f\left( x \right)} \right]_{\max }} = f\left( {2\sqrt 3 } \right) = 144\) ,所以 \({V_{\max }} = 4\sqrt {15} \) .
所以三棱锥 \(P - ABC\) 体积 \(V\) 的最大值为 \(4\sqrt {15} \left( {c{m^3}} \right)\) ,此时 \(x = 2\sqrt 3 \left( {cm} \right)\) .