
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
如图,某校打算在长为1千米的主干道
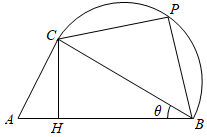
若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让
知识点:第五章 一元函数的导数及其应用
参考答案:\(\frac{{2 + \sqrt 3 }}{4}\);
由题意,在 \(Rt\vartriangle ACB\) 中,可得 \(BC = 1 \times \cos \theta = \cos \theta \) ,
在 \(Rt\vartriangle CBH\) 中,可得 \(CH = \cos \theta \times \sin \theta = \sin \theta \cos \theta \) ,
在 \(Rt\vartriangle CBP\) 中,可得 \(CP = \cos \theta \sin \left( {\frac{\pi }{3} - \theta } \right)\) ,
所以 \(CH + CP = \sin \theta \cos \theta + \cos \theta \sin \left( {\frac{\pi }{3} - \theta } \right)\)\( = \sin \theta \cos \theta + \cos \theta \left( {\frac{{\sqrt 3 }}{2}\cos \theta - \frac{1}{2}\sin \theta } \right)\)
\( = \frac{1}{2}\sin \theta \cos \theta + \frac{{\sqrt 3 }}{2}{\cos ^2}\theta \)\( = \frac{1}{4}\sin 2\theta + \frac{{\sqrt 3 }}{2} \times \frac{{1 + \cos 2\theta }}{2}\)\( = \frac{1}{2}\sin \left( {2\theta + \frac{\pi }{3}} \right) + \frac{{\sqrt 3 }}{4}\) .
因为 \(\theta \in \left[ {\frac{\pi }{{18}},\frac{\pi }{3}} \right)\) ,则 \(\frac{{4\pi }}{9} \leqslant 2\theta + \frac{\pi }{3} < \pi \) ,
所以当且仅当\(2\theta +\frac {\pi } {3}=\frac {\pi } {2}\),即 \(\theta = \frac{\pi }{{12}}\) 时, \(CH + CP\) 取得最大值,且最大值为 \(\frac{{2 + \sqrt 3 }}{4}\) 千米.