
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
如图1所示为一种魔豆吊灯,图2为该吊灯的框架结构图,由正六棱锥\({O_1} - ABCDEF\) 和 \({O_2} - ABCDEF\) 构成,两个棱锥的侧棱长均相等,且棱锥底面外接圆的直径为\(1600\text{mm}\),底面中心为 \(O\) ,通过连接线及吸盘固定在天花板上,使棱锥的底面呈水平状态,下顶点 \({O_2}\) 与天花板的距离为\(1300\text{mm}\),所有的连接线都用特殊的金属条制成,设金属条的总长为 y .
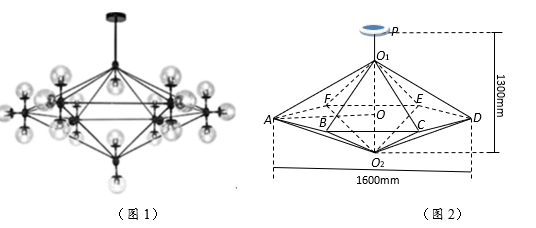
设\(∠{O}_{1}AO=\theta \left ( {\text{rad}} \right )\),当角\(θ\)正弦值的大小是多少时,金属条总长\(y\)最小.
知识点:第五章 一元函数的导数及其应用
参考答案:见解析
解析:
在直角三角形\(OA{O}_{1}\)中, \({O_1}A = \frac{{800}}{{\cos \theta }},O{O_1} = 800\tan \theta \) , \({O_1}P = 1300 - 1600\tan \theta \) ,
由 \(O{O_1} = 800\tan \theta > 0,{O_1}P = 1300 - 1600\tan \theta > 0\) ,所以 \(0 < \tan \theta < \frac{{13}}{{16}}\) ,
所以\(θ\)的范围是 \(0 < \theta < \alpha \) ,其中 \(\tan \alpha = \frac{{13}}{{16}}\) , \(\alpha \in (0,\frac{\pi }{2})\) .
从而有 \(y = 12{O_1}A + 6AB + {O_1}P\)\( = \frac{{12 \times 800}}{{\cos \theta }} + 6 \times 800 + 1300 - 1600\tan \theta \)
\( = \frac{{1600(6 - \sin \theta )}}{{\cos \theta }} + 6100\) ,
所以 \(y = \frac{{1600(6 - \sin \theta )}}{{\cos \theta }} + 6100\) , \(\theta \in (0,\alpha )\)(\(\tan \alpha = \frac{{13}}{{16}}\) , \(\alpha \in (0,\frac{\pi }{2})\)).
令 \(g(\theta ) = \frac{{6 - \sin \theta }}{{\cos \theta }}\) ,所以 \(g'(\theta ) = \frac{{6\sin \theta - 1}}{{{{\cos }^2}\theta }}\) ,
令 \(y' = 0\) ,则 \(\sin \theta = \frac{1}{6}\) ,则 \(\theta = {\theta _0}(tan{\theta _0} = \frac{1}{{\sqrt {35} }})\) .
当 \(\theta \in (0,{\theta _0})\) 时, \(y' < 0\) ;当 \(\theta \in ({\theta _0},\alpha )\) 时, \(y' > 0\) .
函数 \(g(\theta )\) 的单调性与 \(\theta \) 关系列表如下:
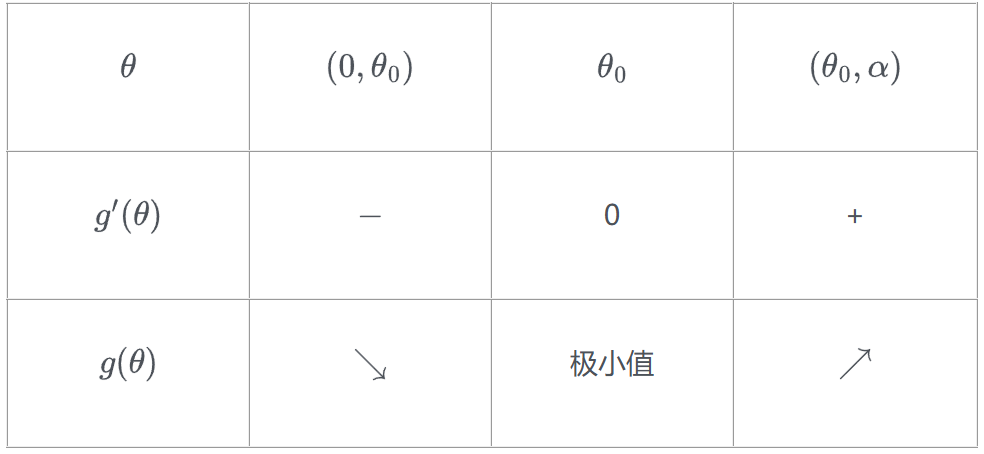
所以当 \(\theta = {\theta _0}\) ,其中 \(\tan {\theta _0} = \frac{{\sqrt {35} }}{{35}}\) 时 \(g(\theta )\) 取得最小值,即\(y\)最小.
故当角 \(\theta \) 满足 \(\sin \theta = \frac{1}{6}\) ( \(\tan \theta = \frac{{\sqrt {35} }}{{35}}\) )时,金属条总长\(y\)最小.