第561题

A.关于原点对称

B.关于\(y\)轴对称

C.关于直线\(x=\pi \)对称

D.关于点\(\left ( {\frac {\pi } {2}，0} \right )\)对称

参考答案：A

第562题

A.16

B.24

C.32

D.48

参考答案：A

第563题

已知函数\(f(x)=2\sin {\left ( {ωx+φ} \right )\left ( {ω>0，0<φ<\frac {\pi } {2}} \right )}\)的图象的相邻两个最高点的距离为\(\frac {\pi } {2}\)，\(f(0)=\sqrt {2}\) ．则（　　）

A.\(ω=\frac {1} {4}\)

B.\(f\left ( {x} \right )\)的图象的对称轴方程为\(x=4k\pi +\frac {\pi } {4}\left ( {k\in Z} \right )\)

C.\(f\left ( {x} \right )\)的图象的单调递增区间为\(\left [ {k\pi -\frac {\pi } {16}，k\pi +\frac {\pi } {16}} \right ]\left ( {k\in Z} \right )\)

D.\(f\left ( {x} \right )\geq -1\)的解集为\(\left [ {\frac {k\pi } {2}-\frac {5\pi } {48}，\frac {k\pi } {2}+\frac {11\pi } {48}} \right ]\left ( {k\in Z} \right )\)

参考答案：D

第564题

若函数\(f\left ( {x} \right )=2\sin {\left ( {2x-\frac {\pi } {3}+φ} \right )}\)是奇函数，则\(φ\)的值可以是（　　）

A.\(\frac {5\pi } {6}\)

B.\(\frac {\pi } {2}\)

C.\(-\frac {2\pi } {3}\)

D.\(-\frac {\pi } {2}\)

参考答案：C

第565题

函数\(f\left ( {x} \right )=\sin {\left ( {ωx+\frac {\pi } {6}} \right )}\left ( {ω>0} \right )\)在\(\left ( {0，\frac {2\pi } {3}} \right )\)单调递增，在\(\left ( {\frac {2\pi } {3}，2\pi } \right )\)单调递减，则\(ω\)的值为（　　）

A.\(\frac {1} {2}\)

B.1

C.2

D.\(\frac {7} {2}\)

参考答案：A

第566题

A.\( - 2\)

B.\( - 1\)

C.\(0\)

D.\(1\)

参考答案：A

解析：

第567题

A.5

B.6

C.7

D.8

参考答案：A

解析：

第568题

A.\(-60\)

B.60

C.\(-240\)

D.240

参考答案：D

解析：

第569题

A.不存在常数项

B.第4项和第5项二项式系数最大

C.第3项的系数最大

D.所有项的系数和为128

参考答案：ABC

解析：

第570题

A.8

B.9

C.10

D.11

参考答案：BCD

解析：

第571题

A.第2项的二项式系数为15

B.\({x^3}\)的系数是240

C.各项二项式系数的和是32

D.各项系数的和是1

参考答案：BD

解析：

第572题

参考答案：1

解析：

第573题

参考答案：\( - \frac{5}{2}\)

解析：

第574题

参考答案：先求得 \({\left( {{x^2} + \frac{1}{{\sqrt x }}} \right)^5}\) 展开式的通项公式，令 \(10 - \frac{5}{2}k = 5\)，求得 k值，代回即可得答案.\({\left( {{x^2} + \frac{1}{{\sqrt x }}} \right)^5}\) 展开式的通项公式为 \({T_{k + 1}} = C_5^k{\left( {{x^2}} \right)^{5 - k}}{\left( {\frac{1}{{\sqrt x }}} \right)^k} = C_5^k{x^{10 - \frac{5}{2}k}}\)，令 \(10 - \frac{5}{2}k = 5\)，解得 \(k = 2\)， 所以展开式中含 \({x^5}\) 的项为 \(C_5^2{x^5} = 10{x^5}\)

第575题

参考答案：令 \(10 - \frac{5}{2}k = 0\),求得k值，代回即可得答案令 \(10 - \frac{5}{2}k = 0\)，解得 \(k = 4\)，所以展开式中常数项为 \(C_5^4 = 5\)

第576题

参考答案：\(\because \)已知 \(f(x) = {(x - \frac{1}{{\sqrt[3]{x}}})^n}\)，\(f\left ( {x} \right )\) 的展开式的各二项式系数的和等于 \({2^n} = 128\)，

\(\therefore n = 7\)．

第577题

参考答案：\(f\left ( {x} \right )\)的展开式中的通项公式为 \({T_{r + 1}} = {\rm{C}}_7^r \cdot {( - 1)^r} \cdot {x^{7 - \frac{{4r}}{3}}},r = 0,1,2, \cdots ,7\)，

第\(r+1\)项的系数为 \({\rm{C}}_7^r \cdot {( - 1)^r}\)，

当该系数最大时，\(r\)为偶数，且 \({\rm{C}}_7^r\) 最大，此时，\(r = 4\)，

故\(f\left ( {x} \right )\)的展开式中系数最大的项为第五项 \({T_5} = 35{x^{\frac{5}{3}}}\)；

第578题

A.30

B.60

C.120

D.150

参考答案：D

解析：

第579题

A.72种

B.144种

C.288种

D.576种

参考答案：B

解析：

第580题

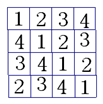
A.432

B.576

C.720

D.864

参考答案：B

解析：