第581题

A.13

B.15

C.17

D.19

参考答案：C

解析：

第582题

A.共有60种不同的坐法

B.空位不相邻的坐法有72种

C.空位相邻的坐法有24种

D.两端不是空位的坐法有27种

参考答案：AC

解析：

第583题

参考答案：18

解析：

第584题

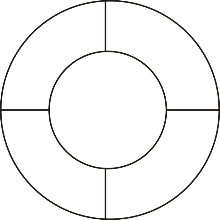
A.36

B.48

C.54

D.72

参考答案：D

解析：

由题意，如图，假设5个区域为分别为1、2、3、4、5，

分2种情况讨论：

\(①\)当选用3种颜色花卉的时，2、4同色且3、5同色，共有涂色方法 \({\rm{C}}_4^3 \cdot {\rm{A}}_3^3 = 24\) 种，

\(②\)当4种不同颜色的花卉全选时，即2、4或3、5用同一种颜色，共有 \({\rm{C}}_2^1 \cdot {\rm{A}}_4^4 = 48\) 种，

则不同的种植方法共有\(24 + 48 = 72\)种；

故选：D.

第585题

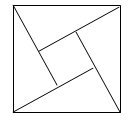
A.120

B.260

C.340

D.420

参考答案：D

解析：

第586题

参考答案：偶数的个位数只能是2、4、6，有 \(A_3^1\) 种排法，其他位上有 \(A_6^3\) 种排法，

由分步乘法计数原理，知共有四位偶数 \({A}^{1}_{3}\cdot {A}^{3}_{6}=360\) (个)；

能被5整除的数个位必须是5，故有 \({A}^{3}_{6}=120\)(个)

第587题

参考答案：最高位上是7时大于6500，有 \(A_6^3\) 种，

最高位上是6时，百位上只能是7或5，故有\(2\times {A}^{2}_{5}\) 种.

由分类加法计数原理知，这些四位数中大于6500的共有 \({A}^{3}_{6}+2\times {A}^{2}_{5}=160\)(个).

第588题

已知\(\sin {α}=\frac {1} {3}\)，且\(α\in \left ( {\frac {π} {2}，π} \right )\)，则\(\frac {\sin {2α}} {\cos {2α+1}}\)（　　）

A.\(-\frac {\sqrt {2}} {4}\)

B.\(2\sqrt {2}\)

C.\(-2\sqrt {2}\)

D.\(\sqrt {2}\)

参考答案：A

第589题

已知θ为锐角，且满足\(\frac {\tan {3θ}} {\tan {θ}}=11\)，则tan2θ的值为（        ）

A.\(\frac {3} {4}\)

B.\(\frac {4} {3}\)

C.\(\frac {2} {3}\)

D.\(\frac {3} {2}\)

参考答案：B

第590题

已知cos（α+\(\frac {π} {6}\)）=\(\frac {3} {5}\)，α∈（0，\(\frac {π} {2}\)），则cos（2α+\(\frac {7π} {12}\)）=___．

参考答案：\(-\frac {31\sqrt {2}} {50}\)

第591题

设f（x）=\(\frac {1} {2}\)cos²x+\(\frac {\sqrt {3}} {2}\)sinxcosx+2，x∈[\(-\frac {π} {6}\)，\(\frac {π} {4}\)]，则f（x）的值域为___．

参考答案：\(\left [ {2，\frac {11} {4}} \right ]\)

第592题

已知\(f(x)=2\sin {\left ( {x+\frac {π} {6}} \right )}\cos {x}-\frac {1} {2}\)，且\(f\left ( {α} \right )=\frac {1} {3}\)，\(α\in \left ( {\frac {π} {6}，\frac {5π} {12}} \right )\)，求cos2α的值.

参考答案：\(\because f(x)=2\sin {\left ( {x+\frac {π} {6}} \right )}\cos {x}-\frac {1} {2}=\sqrt {3}\sin {x\cos {x}}+\cos^{2} {x}-\frac {1} {2}=\frac {\sqrt {3}} {2}\sin {2x}+\frac {1} {2}\cos {2x}=\sin {\left ( {2x+\frac {π} {6}} \right )}\)，\(f\left ( {α} \right )=\frac {1} {3}\)，可得\(\sin {\left ( {2α+\frac {π} {6}} \right )}=\frac {1} {3}\)，\(\because α\in \left ( {\frac {π} {6}，\frac {5π} {12}} \right )\)，可得\(2α+\frac {π} {6}\in \left ( {\frac {π} {2}，π} \right )\)，

\(\therefore \cos {\left ( {2α+\frac {π} {6}} \right )}=-\sqrt {1-\sin^{2} {\left ( {2α+\frac {π} {6}} \right )}}=-\frac {2\sqrt {2}} {3}\)，\(\therefore \cos {2α}=\cos {\left ( {2α+\frac {π} {6}-\frac {π} {6}} \right )}=\cos {\left ( {2α+\frac {π} {6}} \right )}\cos {\frac {π} {6}}+\sin {\left ( {2α+\frac {π} {6}} \right )}\sin {\frac {π} {6}}=-\frac {2\sqrt {2}} {3}\times \frac {\sqrt {3}} {2}+\frac {1} {3}\times \frac {1} {2}=\frac {1-2\sqrt {6}} {6}\)．

第593题

已知α，β∈（0，π），\(\cos {α=\frac {4} {5}}\)，\(\sin {\left ( {α-β} \right )}=\frac {5} {13}\)，求sin（α+β）的值．

参考答案：\(\because \cos {α=\frac {4} {5}}\)，
\(\therefore \cos {2α=2\cos^{2} {α-1}}=\frac {7} {25}\)．
∵α，β∈（0，π），
\(\cos {α}=\frac {4} {5}>0\)，
\(\therefore 0<α<\frac {π} {2}\)，
\(-π<α-β<\frac {π} {2}\)．
又\(\because \sin {\left ( {α-β} \right )}=\frac {5} {13}\)，
\(\therefore α-β\in \left ( {0，\frac {π} {2}} \right )\)，
\(\therefore \cos {\left ( {α-β} \right )}=\frac {12} {13}\)．
\(\therefore \sin {2α}=2\sin {α}\cos {α}=2\times \frac {3} {5}\times \frac {4} {5}=\frac {24} {25}\)．
\(\therefore \sin {\left ( {α+β} \right )}=\sin {\left [ {2α-\left ( {α-β} \right )} \right ]}=\sin {2α}\cos {\left ( {α-β} \right )}-\cos {2α}\sin {\left ( {α-β} \right )}=\frac {24} {25}\times \frac {12} {13}-\frac {7} {25}\times \frac {5} {13}=\frac {253} {325}\)．

第594题

若\(\sin {74°=}m\)，则\(\cos {8°=}\)（　　）

A.\(\sqrt {\frac {1-m} {2}}\)

B.\(\pm \sqrt {\frac {1-m} {2}}\)

C.\(\sqrt {\frac {1+m} {2}}\)

D.\(\pm \sqrt {\frac {1+m} {2}}\)

参考答案：C

第595题

如果\(\left | {\cos {θ}} \right |=\frac {1} {5}\)，\(\frac {5} {2}π<θ<3π\)，那么\(\sin {\frac {θ} {2}}\)的值为（　　）

A.\(\frac {\sqrt {10}} {5}\)

B.\(\frac {\sqrt {15}} {5}\)

C.\(-\frac {\sqrt {10}} {5}\)

D.\(-\frac {\sqrt {15}} {5}\)

参考答案：D

第596题

已知\(θ\)是第三象限角，若\(\sin {θ=-\frac {3} {5}}\)，则\(\tan {\frac {θ} {2}}\)的值为___．

参考答案：\(-3\)

第597题

求证：\(\frac {\sin {4x}} {1+\cos {4x}}\cdot \frac {\cos {2x}} {1+\cos {2x}}\cdot \frac {\cos {x}} {1+\cos {x}}=\tan {\frac {x} {2}}\)

参考答案：证明：
左边\(=\frac {2\sin {2x\cos {2x}}} {2\cos^{2} {2x}}\cdot \frac {\cos {2x}} {2\cos^{2} {x}}\cdot \frac {\cos {x}} {2\cos^{2} {\frac {x} {2}}}
=\frac {\sin {2x}} {4\cos {x\cos^{2} {\frac {x} {2}}}}
=\frac {2\sin {x\cos {x}}} {4\cos {x\cos^{2} {\frac {x} {2}}}}
=\frac {\sin {x}} {2\cos^{2} {\frac {x} {2}}}
=\frac {2\sin {\frac {x} {2}\cos {\frac {x} {2}}}} {2\cos^{2} {\frac {x} {2}}}
=\tan {\frac {x} {2}}
=\)右边

第598题

证明：若α是第四象限角，则\(\sqrt {\frac {1+\sin {α}} {1-\sin {α}}}-\sqrt {\frac {1-\sin {α}} {1+\sin {α}}}=2\tan {α}\)

参考答案：证明：\(\frac {1+\sin {α}} {1-\sin {α}}=\frac {\left ( {1+\sin {α}} \right )^{2}} {\left ( {1-\sin {α}} \right )\left ( {1+\sin {α}} \right )}=\frac {\left ( {1+\sin {α}} \right )^{2}} {1-\left ( {\sin {α}} \right )^{2}}=\frac {\left ( {1+\sin {α}} \right )^{2}} {1-\cos^{2} {α}}\)，因为α是第四象限的角，所以\(\cos {α>0}\)，又因为\(\sin {α<-1}\)，

所以\(1+\sin {α>0}\)，所以\(\sqrt {\frac {1+\sin {α}} {1-\sin {α}}}=\frac {1+\sin {α}} {\cos {α}}\)，同理\(\sqrt {\frac {1-\sin {α}} {1+\sin {α}}}=\frac {1-\sin {α}} {\cos {α}}\)，所以\(\sqrt {\frac {1+\sin {α}} {1-\sin {α}}}-\sqrt {\frac {1-\sin {α}} {1+\sin {α}}}=\frac {1+\sin {α}} {\cos {α}}-\frac {1-\sin {α}} {\cos {α}}=2\frac {\sin {α}} {\cos {α}}=2\tan {α}\)

原式得证．

第599题

化简：\(\sqrt {\frac {1+\sin {α}} {1-\sin {α}}}-\sqrt {\frac {1-\sin {α}} {1+\sin {α}}}\)（α是第二、三象限角）（　　）.

A.\(-\frac {2} {\cos {α}}\)

B.\(\frac {2} {\cos {α}}\)

C.\(-2\tan {α}\)

D.\(2\tan {α}\)

参考答案：C

第600题

已知\(\sin {θ+\cos {θ=\frac {7} {13}}}\)，\(θ\in \left ( {0，π} \right )\)，则\(\sin {θ-\cos {θ=}}\)___．

参考答案：\(\frac {17} {13}\)