
“微信扫一扫”进入题库练习及模拟考试
高中数学必修 第一册(648题)
如图,节日花坛中有5个区域,现有四种不同颜色的花卉可供选择,要求相同颜色的花不能相邻栽种,则符合条件的种植方案有( )种.
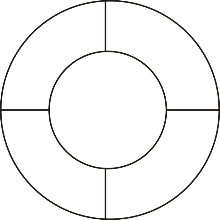
A.36
B.48
C.54
D.72
知识点:第五章 三角函数
参考答案:D
解析:
由题意,如图,假设5个区域为分别为1、2、3、4、5,

分2种情况讨论:
则不同的种植方法共有
故选:D.

“微信扫一扫”进入题库练习及模拟考试
如图,节日花坛中有5个区域,现有四种不同颜色的花卉可供选择,要求相同颜色的花不能相邻栽种,则符合条件的种植方案有( )种.

A.36
B.48
C.54
D.72
参考答案:D
解析:
由题意,如图,假设5个区域为分别为1、2、3、4、5,

分2种情况讨论:
则不同的种植方法共有
故选:D.