
“微信扫一扫”进入考试题库练习及模拟考试
高中数学必修 第一册(648题)
参考答案:\(\frac {49} {81}\)
参考答案:解:由已知得\(\tan {α=\frac {1} {2}}\)
(1)\(\frac {\sin {α-3\cos {α}}} {\sin {α+\cos {α}}}=\frac {\tan {α-3}} {\tan {α+1}}=-\frac {5} {3}\)
(2)\(\sin^{2} {α}+\sin {α}\cdot \cos {α}+2=\sin^{2} {α}+\sin {α}\cdot \cos {α}+2\left ( {\cos^{2} {α}+\sin^{2} {α}} \right )=\frac {3\sin^{2} {α}+\sin {α}\cdot \cos {α}+2\cos^{2} {α}} {\cos^{2} {α}+\sin^{2} {α}}=\frac {3\tan^{2} {α}+\tan {α+2}} {\tan^{2} {α}+1}=\frac {3\times \frac {1} {4}+\frac {1} {2}+2} {\frac {1} {4}+1}=\frac {13} {5}\)
参考答案:(1)\(\frac {\sin {7°+\sin {8°\cdot \cos {15°}}}} {\cos {7°-\sin {8°\cdot \sin {15°}}}}=\frac {\sin {\left ( {15°-8°} \right )+\sin {8°\cdot \cos {15°}}}} {\cos {\left ( {15°-8°} \right )-\sin {8°\cdot \sin {15°}}}}=\frac {\sin {15°\cos {8°}}} {\cos {15°\cos {8°}}}=\tan {\left ( {45°-30°} \right )}=\frac {\tan {45°-\tan {30°}}} {1+\tan {45°\tan {30°}}}=\frac {1-\frac {\sqrt {3}} {3}} {1+1\times \frac {\sqrt {3}} {3}}=2-\sqrt {3}\)
(2)\(4\cos {70°+}\tan {20°=\frac {4\cos {70°\cos {20°+\sin {20°}}}} {\cos {20°}}}=\frac {2\sin {40°+\sin {20°}}} {\cos {20°}}=\frac {2\cos {50°+\sin {\left ( {50°-30°} \right )}}} {\cos {20°}}=\frac {\frac {\sqrt {3}} {2}\sin {50°+\frac {3} {2}\cos {50°}}} {\cos {20°}}=\frac {\sqrt {3}\sin {\left ( {50°+60°} \right )}} {\cos {20°}}=\sqrt {3}\)
A.\(\frac {3\sqrt {3}+4} {10}\)
B.\(\frac {3-4\sqrt {3}} {10}\)
C.\(\frac {3\sqrt {3}-4} {10}\)
D.\(\frac {3+4\sqrt {3}} {10}\)
参考答案:C
A.\(\frac {33} {65}\)
B.\(-\frac {33} {65}\)
C.\(\frac {54} {65}\)
D.\(-\frac {54} {65}\)
参考答案:A
参考答案:\(\frac {4\sqrt {3}-3} {10}\)
参考答案:\(\because \frac {3} {4}π+β-\left ( {\frac {π} {4}-α} \right )=\frac {π} {2}+α+β\),\(\therefore \sin {\left ( {α+β} \right )}=\sin {\left [ {\left ( {\frac {3} {4}π+β} \right )-\left ( {\frac {π} {4}-α} \right )-\frac {π} {2}} \right ]}=\cos {\left [ {\left ( {\frac {3} {4}π+β} \right )-\left ( {\frac {\pi } {4}-α} \right )} \right ]}=-\cos {\left ( {\frac {3} {4}\pi +β} \right )\cos {\left ( {\frac {π} {4}-α} \right )}}-\sin {\left ( {\frac {3} {4}\pi +β} \right )}\sin {\left ( {\frac {π} {4}-α} \right )}\),
\(\because \frac {π} {4}<α<\frac {3} {4}π\),\(\therefore -\frac {π} {2}<\frac {π} {4}-α<0\),\(\therefore \sin {\left ( {\frac {\pi } {4}-α} \right )}=-\frac {4} {5}\),\(\frac {π} {2}<β<\frac {3} {4}π\),\(\because \frac {5π} {4}<\frac {3} {4}\pi +β<\frac {3} {2}π\),\(\therefore \cos {\left ( {\frac {3} {4}π+β} \right )}=-\frac {5} {13}\),\(\therefore \sin {\left ( {α+β} \right )}=\frac {5} {13}\times \frac {3} {5}-\left ( {-\frac {12} {13}} \right )\times \left ( {-\frac {4} {5}} \right )=\frac {15} {65}-\frac {48} {65}=-\frac {33} {65}\)
参考答案:\(\because \sin {\left ( {α+β} \right )}=\frac {\sqrt {5}} {5}\),
\(\therefore \cos {\left ( {α+β} \right )}=\pm \frac {2\sqrt {5}} {5}\),
\(\because α,β\)为锐角,
\(\therefore π>α+β>α>0\),
\(\therefore \sin {α=\frac {3\sqrt {10}} {10}}\),
又\(y=\cos {x}\)在\(\left [ {0,π} \right ]\)上单调递减,
\(\therefore \cos {\left ( {α+β} \right )}<\cos {α=\frac {\sqrt {10}} {10}}\),
\(\therefore \cos {\left ( {α+β} \right )=-\frac {2\sqrt {5}} {5}}\),
\(\therefore \cos {β=}\cos {\left [ {\left ( {α+β} \right )-α} \right ]}=\cos {\left ( {α+β} \right )}\cos {α}+\sin {\left ( {α+β} \right )}\sin {α=\frac {\sqrt {10}} {10}\left ( {-\frac {2\sqrt {5}} {5}} \right )}+\frac {3\sqrt {10}} {10}\cdot \frac {\sqrt {5}} {5}=\frac {\sqrt {2}} {10}\).
第610题
已知
A.\(\frac {1} {12}\)
B.\(\frac {1} {13}\)
C.\(\frac {7} {13}\)
D.\(\frac {12} {13}\)
参考答案:B
第611题
在
A.\(\frac {π} {3}\)
B.\(\frac {2π} {3}\)
C.\(\frac {π} {6}\)
D.\(\frac {π} {4}\)
参考答案:A
参考答案:\(\frac {4} {3}\)
参考答案:\(\tan {\left ( {\frac {π} {4}+α} \right )}=\frac {1+\tan {α}} {1-\tan {α}}=2\),
得\(\tan {α=\frac {1} {3}}\),
因为\(\tan {\left ( {2α-β} \right )}=\tan {\left [ {α+\left ( {α-β} \right )} \right ]}=\frac {\tan {α+\tan {\left ( {α-β} \right )}}} {1-\tan {α\tan {\left ( {α-β} \right )}}}=1\),
又\(α\in \left ( {0,\frac {π} {4}} \right )\),\(β\in \left ( {-\frac {π} {4},0} \right )\),
得\(2α-β\in \left ( {0,\frac {3} {4}π} \right )\),所以\(2α-β=\frac {π} {4}\).
参考答案:\(\because 2α-β=2\left ( {α-β} \right )+β\),又\(\tan {\left ( {α-β} \right )}=\frac {1} {2}\),\(\therefore \tan {2\left ( {α-β} \right )}=\frac {2\tan {\left ( {α-β} \right )}} {1-\tan^{2} {\left ( {α-β} \right )}}=\frac {4} {3}\),
故\(\tan {\left ( {2α-β} \right )}=\tan {\left [ {2\left ( {α-β} \right )+β} \right ]}=\frac {\tan {2\left ( {α-β} \right )+\tan {β}}} {1-\tan {2\left ( {α-β} \right )\tan {β}}}=\frac {\frac {4} {3}-\frac {1} {7}} {1+\frac {4} {3}\times \frac {1} {7}}=1\),又\(\because \tan {α=\tan {\left [ {\left ( {α-β} \right )+β} \right ]}}=\frac {\tan {\left ( {α-β} \right )+\tan {β}}} {1-\tan {\left ( {α-β} \right )+\tan {β}}}=\frac {1} {3}<1\),
且\(0<α<\pi \),\(\therefore 0<α<\frac {\pi } {4}\),\(\therefore 0<2α<\frac {\pi } {2}\),
又\(\tan {β=-\frac {1} {7}}\),且\(β\in \left ( {0,\pi } \right )⇒β\in \left ( {\frac {π} {2},π} \right )⇒-β\in \left ( {-π,-\frac {π} {2}} \right )\).
\(\therefore 2α-β\in \left ( {-π,0} \right )\).又\(\tan {\left ( {2α-β} \right )}=1\),\(\therefore 2α-β=-\frac {3π} {4}\).
第616题
现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( )
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
参考答案:ABD
解析:
解:A. 从中任选1个球,有
B. 若每种颜色选出1个球,有
C. 若要选出不同颜色的2个球,有
D. 若要不放回地依次选出2个球,有
故选:ABD
第617题
若将五本不同的书全部分给三个同学,每人至少一本,则有___种不同的分法.
参考答案:150
解析:
由题意,先将五本书分成三堆,有 \(1,1,3\) 和 \(2,2,1\) 种不同的分法
故有 \(\frac{{C_5^1C_4^1C_3^3}}{{A_2^2}} + \frac{{C_5^2C_3^2C_1^1}}{{A_2^2}}\) 种分堆方式
再分给三个同学,有 \((\frac{{C_5^1C_4^1C_3^3}}{{A_2^2}} + \frac{{C_5^2C_3^2C_1^1}}{{A_2^2}})A_3^3 = 150\) 种不同方法
故答案为:150
第618题
邀请这6人去参加一项活动,必须有人去,去几人自行决定,共有多少种不同的安排方法?
参考答案:由题意,从甲、乙、丙、丁、戊、己6人中,邀请这6人去参加一项活动,必须有人去,共有 \(C_6^1 + C_6^2 + \cdot \cdot \cdot + C_6^6 = {2^6} - 1 = 63\),故共有63种不同的去法.
第619题
将这6人作为辅导员全部安排到3项不同的活动中,求每项活动至少安排1名辅导员的方法总数是多少?
参考答案:该问题共分为三类:第一类:6人中恰有4人分配到其中一项活动中,另外两项活动各分一人,共有 \(C_6^4A_3^3 = 90\) 种;第二类:6人中恰有3人分配到其中一项活动中,共有 \(C_6^3C_3^2A_3^3 = 360\) 种;第三类:6人平均分配到三项活动中,共有 \(C_6^2C_4^2C_2^2 = 90\) 种,所以每项活动至少安排1名辅导员的方法总数为:\(90 + 360 + 90 = 540\)种.
第620题
如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3中的一个. (i)当每条边上的三个数字之和为4时,不同的填法有___种; (ii)当同一条边上的三个数字都不同时,不同的填法有种___.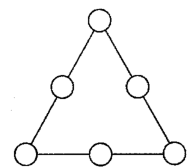
参考答案:4;6
解析:
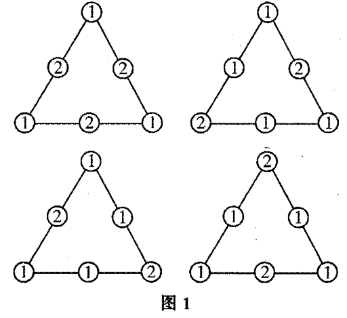
(i)每条边上的三个数字之和为4,填法如图1,共4种;
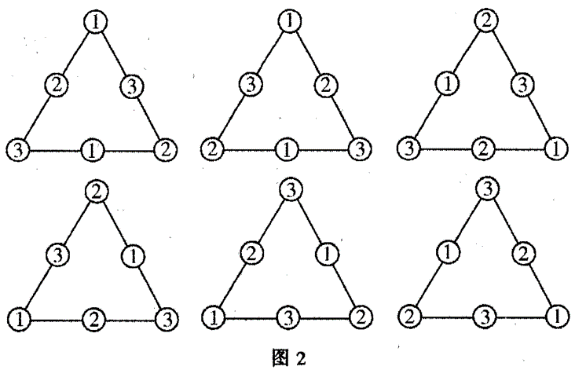
(ii)同一条边上的三个数字都不同时,不同的填法如图2,共6种.
故答案为:4,6.