
“微信扫一扫”进入考试题库练习及模拟考试
高中数学必修 第一册(648题)
第541题
不等式1+tanx≥0的解集是___.
参考答案:\(\left \{ {x|k\pi -\frac {\pi } {4}\leq x<k\pi +\frac {\pi } {2},k\in Z} \right \} \)
参考答案:\((0,1)\)
A.\(1<m\leq 2\)
B.\(1\leq m<2\)
C.\(-2\leq m\leq 2\)
D.\(m\leq 2\)
参考答案:B
第544题
下列函数中,以
A.\(f\left ( {x} \right )=\left | {\cos {2x}} \right |\)
B.\(f\left ( {x} \right )=\sin {\left | {2x} \right |}\)
C.\(f\left ( {x} \right )=\left | {\cos {x}} \right |\)
D.\(f\left ( {x} \right )=\left | {\sin {x}} \right |\)
参考答案:C
A.\(\frac {20} {3}\pi \)
B.\(24\pi \)
C.\(12\pi \)
D.\(\frac {10} {3}\pi \)
参考答案:A
第546题
已知函数
参考答案:\([2k\pi ,2k\pi +\frac {\pi } {2}](k\in Z)\)
第547题
求函数
参考答案:\(f(x) = \sin (\frac{{5\pi }}{6} - 2x) - 2\sin (x - \frac{\pi }{4})\cos (x + \frac{{3\pi }}{4}) = \frac{1}{2}\cos 2x + \frac{{\sqrt 3 }}{2}\sin 2x + (\sin x - \cos x)(\sin x + \cos x) = \sin (2x - \frac{\pi }{6})\)由 \(2k\pi -\frac {\pi } {2}⩽2x-\frac {\pi } {6}⩽2k\pi +\frac {\pi } {2},k\in Z\),解得\(k\pi -\frac {\pi } {6}⩽x⩽k\pi +\frac {\pi } {3},k\in Z\) ,
所以\(f(x)\)的单调增区间为\([k\pi -\frac {\pi } {6},k\pi +\frac {\pi } {3}],k\in Z\) ;
解析:
第548题
若函数
参考答案:
因为
所以
要使
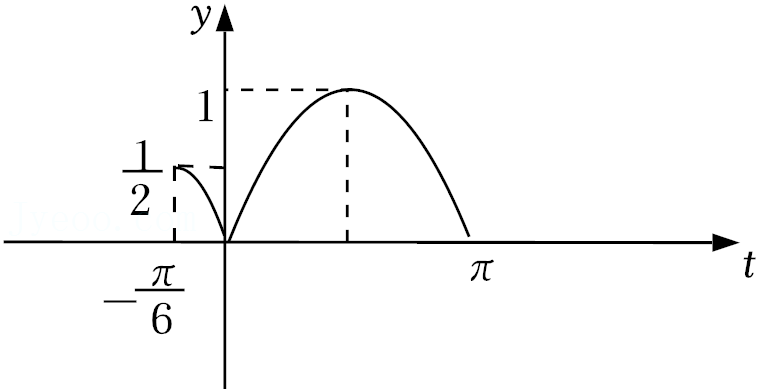
解析:
第550题
求
参考答案:\(\because \) 函数 \(f(x) = {\cos ^2}x + \sqrt 3 \sin x\cos x - \frac{1}{2} = \frac{1}{2}\cos 2x + \frac{{\sqrt 3 }}{2}\sin 2x = \sin (2x + \frac{\pi }{6})\) ,故 \(f(x)\) 的最小正周期为 \(\frac{{2\pi }}{2} = \pi \) .
解析:
第551题
求
参考答案:令\(2k\pi -\frac {\pi } {2}\leq 2x+\frac {\pi } {6}\leq 2k\pi +\frac {\pi } {2}\),求得\(k\pi -\frac {\pi } {3}\leq x\leq k\pi +\frac {\pi } {6},\left ( {k\in Z} \right )\),
可得函数的增区间为\(\left [ {k\pi -\frac {\pi } {3},k\pi +\frac {\pi } {6}} \right ],\left ( {k\in Z} \right )\).
解析:
A.\(\left [ {-\frac {\pi } {6},\frac {\pi } {3}} \right ]\)
B.\(\left [ {\frac {5\pi } {12},\frac {11\pi } {12}} \right ]\)
C.\(\left [ {-\frac {5\pi } {12},\frac {\pi } {12}} \right ]\)
D.\(\left [ {-\frac {11\pi } {12},-\frac {5\pi } {12}} \right ]\)
参考答案:B
参考答案:\((\frac{3}{2},\frac{8}{3})\)
参考答案:\(1 + \sqrt 2 \)
A.1
B.\(\frac {3} {2}\)
C.\(\frac {5} {2}\)
D.3
参考答案:A
A.\((0,\frac {1} {6}]\cup \left [ {\frac {1} {3},\frac {3} {4}} \right ]\)
B.\((0,\frac {1} {3}]\cup \left [ {\frac {2} {3},\frac {3} {4}} \right ]\)
C.\((0,\frac {1} {6}]\cup \left [ {\frac {1} {3},\frac {2} {3}} \right ]\)
D.\((0,\frac {1} {3}]\cup \left [ {\frac {2} {3},\frac {5} {6}} \right ]\)
参考答案:C
第557题
求
参考答案:\(f(x) = \sin (2x - \frac{\pi }{6}) + 2{\cos ^2}x - 1 = \frac{{\sqrt 3 }}{2}\sin 2x - \frac{1}{2}\cos 2x + \cos 2x = \frac{{\sqrt 3 }}{2}\sin 2x + \frac{1}{2}\cos 2x = \sin (2x + \frac{\pi }{6})\)
由 \(2k\pi - \frac{\pi }{2}⩽2x + \frac{\pi }{6}⩽2k\pi + \frac{\pi }{2}(k \in Z)\) ,得\(k\pi -\frac {\pi } {3}⩽x⩽k\pi +\frac {\pi } {6}(k\in Z)\),
所以 \(f(x)\) 的单调增区间是\(\left [ {k\pi -\frac {\pi } {3},k\pi +\frac {\pi } {6}} \right ](k\in Z)\);
解析:
参考答案:\(\because x\in \left [ {0,m} \right ]\),\(2x+\frac {\pi } {6}\in \left [ {\frac {\pi } {6},2m+\frac {\pi } {6}} \right ]\) ,\(f\left ( {x} \right )\in \left [ {\frac {1} {2},1} \right ]\),
\(\therefore \) \(\frac{\pi }{2}⩽2m + \frac{\pi }{6}⩽\frac{{5\pi }}{6}\) ,\(\therefore \) \(\frac{\pi }{6}⩽m⩽\frac{\pi }{3}\) ,
故实数 \(m\) 的取值范围为\(\left [ {\frac {\pi } {6},\frac {\pi } {3}} \right ]\).
解析:
第559题
函数
A.\(\left ( {2kπ-π,2kπ} \right )\),\(k\in Z\)
B.\(\left ( {2kπ,2kπ+π} \right )\),\(k\in Z\)
C.\(\left ( {2kπ-\frac {7π} {6},2kπ-\frac {π} {6}} \right )\),\(k\in Z\)
D.\(\left ( {2kπ-\frac {π} {6},2kπ+\frac {5π} {6}} \right )\),\(k\in Z\)
参考答案:C
A.\(2\pi \)
B.\(\pi \)
C.\(\frac {π} {2}\)
D.\(\frac {π} {4}\)
参考答案:B