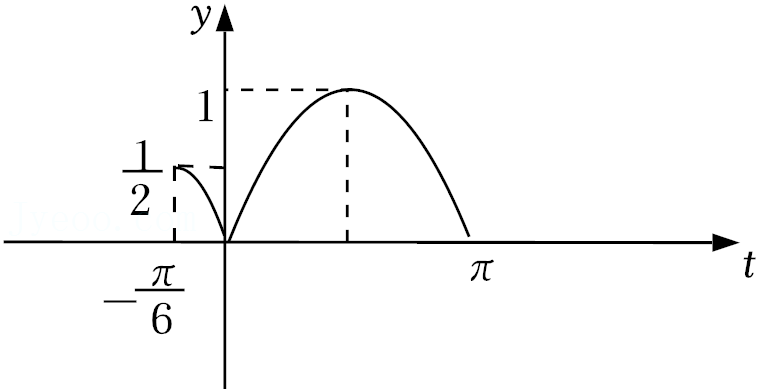
因为\(x \in [0,\frac{{7\pi }}{{12}})\),所以设\(t = 2x - \frac{\pi }{6}\) ,则\(t \in [ - \frac{\pi }{6},\pi )\) ,
所以 \(f(x) = \sin (2x - \frac{\pi }{6}) \in [ - \frac{1}{2},1]\),\(y = |\sin t|\) 的图象如图,
要使\(y = |\sin t| - m\)在\([ - \frac{\pi }{6},\pi )\)有两个零点,则\(\frac{1}{2} < m < 1\),故\(m\)的取值范围是\(\left ( {\frac {1} {2},1} \right )\).