第481题

参考答案：\((\frac{\pi }{4},\frac{{3\pi }}{4})\bigcup {(\frac{{5\pi }}{4},\frac{{7\pi }}{4})} \)

第482题

参考答案：①当 \(m > 0\) 时， \(r = \sqrt {{m^2} + 8{m^2}} = 3m\)，

\(\sin {\theta }=\frac {2\sqrt {2}m} {3m}=\frac {2\sqrt {2}} {3}，\cos {\theta }=\frac {m} {3m}=\frac {1} {3}，\tan {\theta }=\frac {2\sqrt {2}m} {m}=2\sqrt {2}\)．

②当 \(m < 0\) 时，\(r = \sqrt {{m^2} + 8{m^2}} = - 3m\)，

有 \(\sin {\theta }=\frac {2\sqrt {2}m} {-3m}=-\frac {2\sqrt {2}} {3}，\cos {\theta }=\frac {m} {-3m}=-\frac {1} {3}，\tan {\theta }=\frac {2\sqrt {2}m} {m}=2\sqrt {2}\)．

第483题

已知点 \(P(x,1)\) 为角 \(\alpha \) 终边上一点．若角 \(\alpha \) 是第二象限角， \(\sin \alpha = \frac{{\sqrt 3 }}{3}\) ，则 \(x\) 的值为(  )

A.\(\sqrt {3}\)

B.\(-\sqrt {3}\)

C.\(\sqrt {2}\)

D.\(-\sqrt {2}\)

参考答案：D

第484题

如果点\(P\left ( {2\sin {θ，\sin {θ\cdot \cos {θ}}}} \right )\)位于第四象限，那么角\(θ\)所在象限为（  ）

A.第一象限

B.第二象限

C.第三象限

D.第四象限

参考答案：B

第485题

利用单位圆和三角函数线，求满足条件\(\left \{ \begin{gathered} {\cos {x\leq -\frac {\sqrt {2}} {2}}} \\ {\sin {x\geq \frac {1} {2}}} \end{gathered} \right .\)成立的\(x\)的集合．

参考答案：单位圆中的三角函数线同时

满足\(\sin {x\geq \frac {1} {2}}，\cos {x\leq -\frac {\sqrt {2}} {2}}\)的\(x\)是\(\left \{ \begin{gathered} {2kπ+\frac {π} {6}\leq x\leq 2kπ+\frac {5π} {6}} \\ {2kπ+\frac {3π} {4}\leq x\leq 2kπ+\frac {5π} {4}} \end{gathered} \right .\)，

\(k\in Z\)；

即\(x\)的取值范围是\(\left \{ {x|2kπ+\frac {3π} {4}\leq x\leq 2kπ+\frac {5\pi } {6}，k\in Z} \right \} \)．

第486题

参考答案：1

第487题

参考答案：\( - 1\)

第488题

参考答案：2

第489题 求证： \(2\left ( {1-\sin {α}} \right )\left ( {1+\cos {α}} \right )=\left ( {1-\sin {α+\cos {α}}} \right )^{2}\)

参考答案：证明：
左边=\(2-2\sin {α}+2\cos {α-2\sin {α}}\cos {α}\)
\(=1+\sin^{2} {α}+\cos^{2} {α}-2\sin {α\cos {α+2\left ( {\cos {α-\sin {α}}} \right )}}\)
\(=1+2\left ( {\cos {α-\sin {α}}} \right )+\left ( {\cos {α-\sin {α}}} \right )^{2}\)
=\(\left ( {1-\sin {α+\cos {α}}} \right )^{2}\)
= 右边

第490题

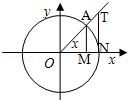
参考答案：（1）在单位圆中，有 \({S_{\Delta OAN}} < {S_{扇形OAN}} < {S_{\Delta ONT}}\)，\(\therefore \)\(\frac{1}{2}ON \cdot MA < \frac{1}{2}ON \cdot x < \frac{1}{2}ON \cdot NT\)， 即\(MA < x < NT\)， 又 \(\sin x = MA\)，\(\cos x = OM\)，\(\tan x = NT\)，\(\therefore \sin x < x < \tan x\)；

解析：

第491题

\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2010}\)

参考答案：

（2）\(\because \)\(\frac {1} {2}，\frac {2} {3}，\frac {3} {4}，\frac {2010} {2011}\) 均为小于 \(\frac{\pi }{2}\) 的正数， \(\sin \frac {1} {2}<\frac {1} {2}，\sin \frac {2} {3}<\frac {2} {3}，\sin \frac {3} {4}<\frac {3} {4}，\sin \frac {2010} {2011}<\frac {2010} {2011}\) ，

将以上2010道式相乘得\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2}\cdot \frac {2} {3}\cdot \frac {3} {4}\cdots \frac {2010} {2011}=\frac {1} {2011}<\frac {1} {2010}\)，

即\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2010}\)．

解析：

第492题

参考答案：\(\frac {\sin {760°}} {\sqrt {1-\cos^{2} {40°}}}=\frac {\sin {\left ( {2\times 360°+40°} \right )}} {\sqrt {\sin^{2} {40°}}}=\frac {\sin {40°}} {\left | {\sin {40°}} \right |}=\frac {\sin {40°}} {\sin {40°}}=1\)

解析：

第493题

参考答案：\(\tan {α\sqrt {\frac {1} {\sin^{2} {α}}-1}}=\tan {α}\sqrt {\frac {1-\sin^{2} {α}} {\sin^{2} {α}}}=\tan {α\sqrt {\frac {\cos^{2} {α}} {\sin^{2} {α}}}}=\frac {\sin {α}} {\cos {α}}\cdot \frac {-\cos {α}} {\sin {α}}=-1\)

解析：

第494题

参考答案：0

第495题

参考答案：\(-\frac {2} {\sin {θ}}\)

第496题

参考答案：\(-\frac {2} {\sin {x}}\)且\(x\ne 2k\pi +\frac {\pi } {2}(k\in Z)\)

第497题

参考答案：\(\frac {\pi } {3}\)

第498题

参考答案：左边\( = ({\sin ^2}\alpha - {\cos ^2}\alpha )({\sin ^2}\alpha + {\cos ^2}\alpha ) = {\sin ^2}\alpha - {\cos ^2}\alpha = {\sin ^2}\alpha - (1 - {\sin ^2}\alpha ) = 2{\sin ^2}\alpha - 1 = \) 右边

解析：

第499题

参考答案：左边 \( = {\sin ^2}\alpha (1 - {\sin ^2}\beta ) + {\sin ^2}\beta + {\cos ^2}\alpha {\cos ^2}\beta \) \(={\sin^{2}}\alpha {\cos^{2}}\beta +{\sin^{2}}\beta +{\cos^{2}}\alpha {\cos^{2}}\beta \)

\( = {\cos ^2}\beta ({\sin ^2}\alpha + {\cos ^2}\alpha ) + {\sin ^2}\beta \) \( = {\cos ^2}\beta + {\sin ^2}\beta \) \( = 1\) \( = \) 右边

解析：

第500题

参考答案：由 \(\cos x + \sin x = \frac{1}{5}\) ，两边平方得： \(co{s^2}x + si{n^2}x + 2\cos x\sin x = \frac{1}{{25}}\)

\(\therefore \) \(1 + 2\cos x\sin x = \frac{1}{{25}}\) 即 \(\cos x\sin x = - \frac{{12}}{{25}}\)

\(\because \cos x\sin x < 0\) 且 \(-\pi <x<0，\therefore x\) 为第四象限角．

解析：