第441题

参考答案：设 \( g\left(x\right)=\frac{3-x}{3+x}=-1+\frac{6}{x+3}\)
设 \( {x}_{1},{x}_{2}\in (-\mathrm{3,3})\)，且 \( {x}_{1}<{x}_{2}\)
\( \therefore g\left({x}_{1}\right)-g\left({x}_{2}\right)=-1+\frac{6}{{x}_{1}+3}+1-\frac{6}{{x}_{2}+3}\)\( =\frac{6({x}_{2}-{x}_{1})}{({x}_{1}+3)({x}_{2}+3)}\)
\( \because -3<{x}_{1}<{x}_{2}<3\)\( \therefore {x}_{2}-{x}_{1}>0,{x}_{1}+3>0,{x}_{2}+3>0\)\( \therefore g\left({x}_{1}\right)-g\left({x}_{2}\right)>0\)
即\( g\left({x}_{1}\right)>g\left({x}_{2}\right)\)
\( \therefore g\left(x\right)\) 在 \( (-\mathrm{3,3})\) 上单调递减
又 \( 0<a<1\)
\( \therefore f\left(x\right)\) 在 \( (-\mathrm{3,3})\) 上单调递增

第442题

参考答案：由（2）可知 \( f\left(x\right)\) 在 \( (-\mathrm{2,2})\) 上单调递增

\(\therefore c\le \left [ {f} \right (m)+f(n){]}_{\text{max}}\) 即可

\( \therefore c\le 2f\left(2\right)=-2{\mathrm{log}}_{a}5\)

第443题

参考答案：由题意可知：\( f\left(x\right)\)是奇函数，则有
\( f(-x)+f\left(x\right)=0\)
即 \( {\mathrm{log}}_{\frac{1}{2}}\left(\frac{1-ax}{x-1}\right)+{\mathrm{log}}_{\frac{1}{2}}\left(\frac{1+ax}{-x-1}\right)=0\)
\( \therefore \frac{(1-ax)(1+ax)}{-(x-1)(x+1)}=1\)
\( \therefore 1-{a}^{2}{x}^{2}=-({x}^{2}-1)\)\( \therefore {a}^{2}{x}^{2}={x}^{2}\)\( \therefore a=\pm 1\)
经检验，当 \( a=1\) 时，不满足题意
\( \therefore a=-1\)

第444题

参考答案：由（1）可知 \( f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(\frac{1+x}{x-1}\right)\)设 \( g\left(x\right)=\frac{1+x}{x-1}=1+\frac{2}{x-1}\)若 \( f\left(x\right)\) 在 \( (1,+\infty )\) 内单调递增，则说明 \( g\left(x\right)\) 在 \( (1,+\infty )\) 内单调递减，下面证明之：设\( 1<{x}_{1}<{x}_{2}\)则\( g\left({x}_{1}\right)=1+\frac{2}{{x}_{1}-1},g\left({x}_{2}\right)=1+\frac{2}{{x}_{2}-1}\)那么\( g\left({x}_{1}\right)-g\left({x}_{2}\right)=(1+\frac{2}{{x}_{1}-1})-(1+\frac{2}{{x}_{2}-1})\)\( \text{ }=\frac{2({x}_{2}-{x}_{1})}{({x}_{1}-1)({x}_{2}-1)}\) \( \because 1<{x}_{1}<{x}_{2}\)\( \therefore {x}_{1}-1>0,{x}_{2}-1>0,{x}_{2}-{x}_{1}>0\) \( \therefore g\left({x}_{1}\right)-g\left({x}_{2}\right)>0\) 即 \( g\left({x}_{1}\right)>g\left({x}_{2}\right)\)即函数 \( g\left(x\right)\) 在 \( (1,+\infty )\) 内单调递减故函数 \( f\left(x\right)\) 在 \( (1,+\infty )\) 内单调递增

第445题

参考答案：由题意可知 \( f\left(x\right)>(\frac{1}{2}{)}^{x}+m\) 恒成立

只需 \(\left [ {f} \right (x)-(\frac {1} {2}{)}^{x}{]}_{\text{min}}>m\) 即可

由（2）可知 \( f\left(x\right)\) 在 \( (1,+\infty )\) 内单调递增

\( \therefore f\left(x\right)\) 在 \( \left[\mathrm{3,4}\right]\) 上单调递增

而 \( y=(\frac{1}{2}{)}^{x}\) 在 \( \left[\mathrm{3,4}\right]\) 上单调递减

\( \therefore y=-(\frac{1}{2}{)}^{x}\) 在 \( \left[\mathrm{3,4}\right]\) 上单调递增

\( \therefore \)当 \( x=3\) 时，\(\left [ {f} \right (x)-(\frac {1} {2}{)}^{x}{]}_{\text{min}}=-\frac {9} {8}\)

\( \therefore m<-\frac{9}{8}\)

故实数 \( m\) 的取值范围是 \( (-\infty ,-\frac{9}{8})\)

第446题

A.\( 1<d<c<a<b\)

B.\( c<d<1<a<b\)

C.\( c<d<1<b<a\)

D.\( d<c<1<a<b\)

参考答案：B

第447题

A.\(a<b<c\)

B.\(c<b<a\)

C.\(b<c<a\)

D.\(b<a<c\)

参考答案：D

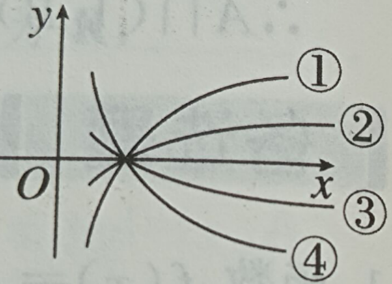
第448题

参考答案：\({C_1}\) 对应的函数为 \(g\left( x \right)={x^3}\) ， \({C_2}\) 对应的函数为 \(f\left( x \right)={2^x}\) .

第449题

参考答案：因为 \(f\left( 1 \right) > g\left( 1 \right)\) ，
\(f\left( 2 \right) < g\left( 2 \right)\) ，
\(f\left( 9 \right) < g\left( 9 \right)\) ，
\(f\left( {10} \right) > g\left( {10} \right)\) ，所以 \(1 < {x_1} < 2\) ，
\(9 < {x_2} < 10\) ，所以 \({x_1} < 6 < {x_2}\) ，
\(2{\rm{ }}019 > {x_2}\) ，从图象上可以看出当 \({x_1} < x < {x_2}\) 时，
\(f\left( x \right) < g\left( x \right)\) ，所以 \(f\left( 6 \right) < g\left( 6 \right)\) ；当 \(x > {x_2}\) 时，
\(f\left( x \right) > g\left( x \right)\) ，所以 \(f\left( {2{\rm{ }}019} \right) > g\left( {2{\rm{ }}019} \right)\) ；
又因为 \(g\left( {2{\rm{ }}019} \right) > g\left( 6 \right)\) ，所以 \(f\left( {2{\rm{ }}019} \right) > g\left( {2{\rm{ }}019} \right) > g\left( 6 \right) > f\left( 6 \right)\) ．

第450题

A.

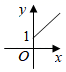
B.

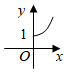
C.

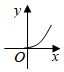
D.

参考答案：D

第451题

参考答案：根据题意，得 \(\frac{4}{5}{p_0} = {p_0}{e^{ - k}}\) ，\( \therefore {e}^{-k}=\frac{4}{5}\)，\( \mathrm{p}\left(t\right)={p}_{0}{\left(\frac{4}{5}\right)}^{t}\).

第452题

参考答案：由 \(p\left ( {t} \right )={p}_{0}\left ( {\frac {4} {5}} \right )^{t}\le \frac {1} {1000}{p}_{0}\)得\( {\left(\frac{4}{5}\right)}^{t}\le {10}^{-3}\)

两边取对数并整理得\(t\left ( {1-3\lg {2}} \right )\ge 3\) ，\( \mathrm{t}\ge 30\). 因此，至少还需过滤 30 个小时.

第453题

A.\( 1.2\)天

B.\( 1.8\)天

C.\( 2.5\)天

D.\( 3.5\)天

参考答案：B

第454题

A.\( \frac{1}{10}\)

B.\( \sqrt{10}\)

C.\( \frac{\sqrt{10}}{10}\)

D.10

参考答案：C

第455题

A.\( \left(3,+\infty \right)\)

B.\( \left(\mathrm{2,3}\right)\)

C.\( \left(\mathrm{1,2}\right)\)

D.\( \left(\mathrm{0,1}\right)\)

参考答案：B

第456题

A.\( \left(\mathrm{1,3}\right)\)

B.\( \left(\mathrm{1,2}\right)\)

C.\( \left(\mathrm{0,3}\right)\)

D.\( \left(\mathrm{0,2}\right)\)

参考答案：C

第457题

参考答案：\( \pm 2\)

第458题

参考答案：1

第459题

参考答案：\(4\)

第460题

参考答案：\(\because y = f(x)\) 是偶函数， \(\therefore f( - x) = f(x)\) ，

\(\therefore {\log _3}({3^{ - x}} + 1) - \frac{1}{2}kx = {\log _3}({3^x} + 1) + \frac{1}{2}kx\)

化简得\( {\mathrm{log}}_{3}\left(\frac{{3}^{-x}+1}{{3}^{x}+1}\right)=kx\)，即\( {\mathrm{log}}_{3}\frac{1}{{3}^{x}}=kx\)，\( {\mathrm{log}}_{3}{3}^{-x}=kx\)， \(\therefore - x = kx\) ， ，

即 \((k + 1)x = 0\) 对任意的 \(x \in R\) 都成立， \(\therefore k = - 1\) ；