高中数学必修 第一册(648题)
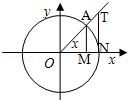
已知\(0<x<\frac {\pi } {2}\),用单位圆求证下面的不等式:
\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2010}\)
知识点:第五章 三角函数
参考答案:
(2)\(\because \)\(\frac {1} {2},\frac {2} {3},\frac {3} {4},\frac {2010} {2011}\) 均为小于 \(\frac{\pi }{2}\) 的正数, \(\sin \frac {1} {2}<\frac {1} {2},\sin \frac {2} {3}<\frac {2} {3},\sin \frac {3} {4}<\frac {3} {4},\sin \frac {2010} {2011}<\frac {2010} {2011}\) ,
将以上2010道式相乘得\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2}\cdot \frac {2} {3}\cdot \frac {3} {4}\cdots \frac {2010} {2011}=\frac {1} {2011}<\frac {1} {2010}\),
即\(\sin {\frac {1} {2}}\cdot \sin {\frac {2} {3}}\cdot \sin {\frac {3} {4}}\cdot \cdots \cdot \sin {\frac {2010} {2011}}<\frac {1} {2010}\).
解析:



