第301题

A.\( \left(\mathrm{1,9}\right]\)

B.\( \left(\mathrm{1,25}\right]\)

C.\( \left[\mathrm{4,25}\right]\)

D.\( [4,+\infty )\)

参考答案：B

第302题

参考答案：设每天从报社买进\(x(250≤x≤400)\)份报纸，每月所获利润是\(y\)元，则每月售出报纸共\((20x+10×250)\)份，每月退回报社报纸共\(10×(x-250)\)份．

依题意得\(y=(0.40-0.24)×(20x+10×250)-(0.24-0.08)×10(x-250)\)．即\(y=0.16(20x+2500)-0.16(10x-2500)\)，

化简得\(y=1.6x+800(250≤x≤400)\)．\(∵\)此一次函数\((y=kx+b，k≠0)\)的\(k=1.6>0\)，\(∴y\)是一个增函数，

再由\(250≤x≤400\)知当\(x=400\)时，\(y\)取得最大值，此时\(y=1.6×400+800=1440\)，\(∴\)每天买进400份报纸时获利最大，最多可获利1440元．

第303题

A.40分钟

B.35分钟

C.30分钟

D.25分钟

参考答案：C

第304题

参考答案：根据每户的用电单价与户年用电量的关系表，可以得出：当\(0<x≤2640\)时，\(f(x)=0.5x\)；当\(2640<x≤3720\)时，\(f(x)=0.5×2640+0.55(x-2640)=0.55x-132\)；当\(x>3720\)时，\(f(x)=0.5×2640+0.55×(3720-2640)+0.8(x-3720)=0.8x-1062\)，所以

\( f\left(x\right)＝\left\{\begin{array}{c}0.5x，0<x\le 2640\\ 0.55x-132，2640<x\le 3720\\ 0.8x-1062，x>3720\end{array}\right.\)

第305题

参考答案：因为\(2640<3000<3720\)，所以范伟一家2019年应缴纳电费\(0.55×3000-132=1518\)(元)．

第306题

参考答案：显然张莉一家在2019年的用电量大于2640度，若张莉一家在2019年用了3720度电，则所缴的电费为\(0.55×3720-132＝1914\)(元)，\(1914<1942\)，所以张莉一家在2019年的用电量大于3720度，所以设张莉一家在2019年用的电为x度，则\(x>3720\)，且\(0.8x-1062=1942\)，解得\(x=3755\)，所以张莉一家在2019年用了3755度电．

第307题

参考答案：\(x\)的取值范围为\( \left\{x|10\le x\le 90\right\}\)．

第308题

参考答案：\(y=0.25\times {x}^{2}\times 20+0.25\times {(100-x)}^{2}\times 10=\frac {15} {2}{x}^{2}-500x+25000(10\le x\le 90)\)．

第309题

参考答案：\(\mathrm{y}=\mathrm{}\frac {15} {2}{x}^{2}-500x+25000=\frac {15} {2}\left ( {x-\frac {100} {3}} \right )^{2}+\frac {50000} {3}\)，当\( \mathrm{x}=\frac{100}{3}\)时，\(y\)取得最小值，\({y}_{\text{min}}=\frac {50000} {3}\)，故发电站建在距\(A\)城\( \frac{100}{3}\) km处，能使月供电总费用\(y\)最少．

第310题

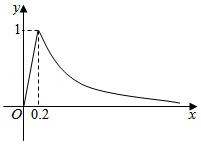
A.当\( 0⩽x⩽0.2\)时，\( y=5x\)

B.当\( x>0.2\)时，\( y=\frac{1}{5x}\)

C.教室内持续有效杀灭病毒时间为\( 0.85\)小时

D.喷洒药物\( 3\)分钟后才开始有效灭杀病毒

参考答案：ABD

第311题

参考答案：月产量为x台，则总成本为\((20000+100x)\)元，

那么\( f\left(x\right)＝\left\{\begin{array}{c}-\frac{1}{2}{x}^{2}+300x-2000，0\le x\le 400，x\in N\\ 60000-100x，x>400，x\in N\end{array}\right.\)

第312题

参考答案：当\( 0\le x\le 400\)时，\(f\left ( {x} \right )=-\frac {1} {2}{(x-300)}^{2}+25000\)，所以当\(x=300\)时，\(f(x)\)有最大值为25000；

当\(x>400\)时，\(f(x)\)是减函数，且\(f(x)<60000-100×400=20000\)，所以当\(x=300\)时，\(f(x)\)的最大值为25000，即当月产量为300台时，公司所获的利润最大，最大利润为25000元.

第313题

参考答案：由\( \mathrm{g}\left(n\right)=\frac{k}{\sqrt{n+1}}\)，当\(n=0\)时，由题意，可得\(k=8\)，所以\(f\left ( {n} \right )=\left ( {100+10n} \right )\left ( {10-\frac {8} {\sqrt {n+1}}} \right )-100n\) (\( n\in \mathbf{Z}\)且\( n\ge 0\))

第314题

参考答案：2)由\(f\left ( {n} \right )=\left ( {100+10n} \right )\left ( {10-\frac {8} {\sqrt {n+1}}} \right )-100n=1000-80\left ( {\sqrt {n+1}+\frac {9} {\sqrt {n+1}}} \right )\le 1000-80\times 2\sqrt {9}=520\)，当且仅当\( \sqrt{n+1}=\frac{9}{\sqrt{n+1}}\)，即\(n=8\)时取等号，所以第8年工厂的利润最高，最高为520万元

第315题

参考答案：长方体底面积\(\mathrm{S}=\frac {800} {8}=100{米}^{2}\)，地面一边长为\(x\)米，因此另一边长为\( \frac{100}{x}\)米，

池壁总面积为\(8\cdot \left ( {2x+\frac {200} {x}} \right ){米}^{2}\)米²，
∴ 总造价\(y=100\times 2a+\left ( {2x+\frac {200} {x}} \right )\cdot 8\cdot a=200a+16a\left ( {x+\frac {100} {x}} \right )\left ( {x>0} \right )\)．

\(∵\)函数\( \mathrm{y}=200a+16a\left(x+\frac{100}{x}\right)\)在\((0，10]\)上是减函数，在\((10，+∞)\)上是增函数，
\(∴\)当\(x=10\)时，总造价最低，且\({y}_{\text{min}}=520a\) (元)．

第316题

参考答案：\( y=\frac{{t}^{2}-4t+1}{t}=t+\frac{1}{t}-4\ge -2(\because t>0)\)，当且仅当\( t=1\)时，\({y}_{\text{min}}=-2.\)

第317题

参考答案：当\( a\ge 0\)时，\( f\left(x\right)=x+\frac{a}{x}+2>0\)恒成立；
当\( a<0\)时，\(f\left ( {x} \right )=x+\frac {a} {x}+2\ge 1+a+2=3+a>0\)，所以\( a>-3\).

第318题

参考答案：\( f\left(0\right)=0\)，故\( 0\ge a+1⟹a\le -1\)；
当\( x>0\)时，\( f\left(x\right)=9x+\frac{{a}^{2}}{x}-7\ge a+1\)，
即\( 6\left|a\right|\ge a+8\)，又\( a\le -1\)，故\( a\le -\frac{8}{7}\).

第319题

参考答案：\( x\in \left[\mathrm{1,4}\right], x+\frac{4}{x}\in \left[\mathrm{4,5}\right]\),分类讨论：

(1)当\( a\ge 5\)时，\( f\left(x\right)=a-x-\frac{4}{x}+a=2a-x-\frac{4}{x}\)，函数的最大值\( 2a-4=5, \therefore a=\frac{9}{2}\)，舍去；

(2)当\( a\le 4\)时，\( f\left(x\right)=x+\frac{4}{x}-a+a=x+\frac{4}{x}\le 5\)，此时命题成立；

当\( 4<a<5\)时，\(\left [ {f\left ( {x} \right )} \right ]_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{m}\mathrm{a}\mathrm{x}\{ \left | {4-a} \right |+a，\left | {5-a} \right |+a\} \)，则

\( \left\{\begin{array}{c}\left|4-a\right|+a\ge \left|5-a\right|+a\\ \left|4-a\right|+a=5\end{array}\right.\)或\( \left\{\begin{array}{c}\left|4-a\right|+a<\left|5-a\right|+a\\ \left|5-a\right|+a=5\end{array}\right.\)

解得\( a=\frac{9}{2}\)或\( a<\frac{9}{2}\).

综上可得，实数\( a\) 的取值范围是\( (-\infty ,\frac{9}{2}]\).

第320题

参考答案：\(-\sqrt[{4}] {a-1}\)；\(-3\)