第341题

A.第一、二、三象限

B.第一、三、四象限

C.第二、三、四象限

D.第一、二、四象限

参考答案：A

第342题

A.\(\left( {1, + \infty } \right)\)

B.

C.\(\left( {3, + \infty } \right)\)

D.\(\left( { - \infty ,3} \right)\)

参考答案：A

第343题

A.

B.

C.

D.

参考答案：D

第344题

A.任意的 \({x-1},{x-2} \in R\) 且 \({x-1} \ne {x-2}\) ，都有 \(\frac{{f\left( {{x-1}} \right) - f\left( {{x-2}} \right)}}{{{x-1} - {x-2}}} < 0\)

B.任意的 \({x-1},{x-2} \in R\) 且 \({x-1} \ne {x-2}\) ，都有 \(\frac{{g\left( {{x-1}} \right) - g\left( {{x-2}} \right)}}{{{x-1} - {x-2}}} < 0\)

C.\(f\left( x \right)\) 有最小值，无最大值

D.\(g\left( x \right)\) 有最小值，无最大值

参考答案：ABC

第345题

A.\(f\left( { - x} \right) + g\left( { - x} \right) = g\left( x \right) - f\left( x \right)\)

B.\(f\left( { - 2} \right) < f\left( 3 \right)\)

C.\(f\left( x \right) - g\left( x \right) = {\pi ^{ - x}}\)

D.\(f\left( {2x} \right) = 2f\left( x \right)g\left( x \right)\)

参考答案：ABD

第346题

参考答案：6

第347题

参考答案：\(\left[ {6, + \infty } \right)\)

第348题

参考答案：\(\left[ { - \frac{3}{4}, + \infty } \right)\)

第349题

参考答案：解：函数 \(y = {a^{2x}} + 2{a^x} - 1 = {\left( {{a^x} + 1} \right)^2} - 2,\) \(x \in \left[ { - 1,1} \right]\)．若 \(a > 1\)，则\(x = 1\)时，函数取最大值 \({a^2} + 2a - 1 = 14\)，解得 \(a = 3\)若 \(0 < a < 1\)，则\(x = - 1\)时，函数取最大值 \({a^{ - 2}} + 2{a^{ - 1}} - 1 = 14\)，解得 \(a = \frac{1}{3}\)综上所述，\(a = 3\) 或 \(a = \frac{1}{3}\)

第350题

参考答案：因为 \(f(x)\) 为 \(R\) 上的奇函数，所以 \(f(0) = 0\)，得 \(b = 1\).又 \(f( - 1) = - f(1)\)，所以 \(a = 1\).

第351题

参考答案：证明：由(1)知 \(f(x) = \frac{{1 - {2^x}}}{{1 + {2^x}}}\) .任取 \({x_1},{x_2} \in R\)，且 \({x_1} < {x_2}\), 则 \(\begin{gathered}
f({x_1}) - f({x_2}) \\
= \frac{{1 - {2^{{x_1}}}}}{{1 + {2^{{x_1}}}}} - \frac{{1 - {2^{{x_2}}}}}{{1 + {2^{{x_2}}}}} \\
= \frac{{\left( {1 - {2^{{x_1}}}} \right)\left( {1 + {2^{{x_2}}}} \right) - \left( {1 - {2^{{x_2}}}} \right)\left( {1 + {2^{{x_1}}}} \right)}}{{\left( {1 + {2^{{x_1}}}} \right)\left( {1 + {2^{{x_2}}}} \right)}} \\
= \frac{{2\left( {{2^{{x_2}}} - {2^{{x_1}}}} \right)}}{{\left( {1 + {2^{{x_1}}}} \right)\left( {1 + {2^{{x_2}}}} \right)}} \\
\end{gathered} \) \(\begin{gathered}
\because {x_1} < {x_2} \\
\therefore {2^{{x_2}}} - {2^{{x_1}}} > 0 \\
\end{gathered} \)又 \(\left( {{2^{{x_1}}} + 1} \right)\left( {{2^{{x_2}}} + 1} \right) > 0\)故 \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\) ，即 \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\) ，所以 \(f(x)\) 为 \(R\) 上的减函数．

第352题

参考答案：因为\(f(x)\)为减函数，所以不等式 \(f({t^2} - 2t) < f( - 2{t^2} + k)\) 恒成立，即 \({t^2} - 2t > k - 2{t^2}\) 恒成立，即 \(k < 3{t^2} - 2t\)恒成立，而\(3{t^2} - 2t = 3{\left( {t - \frac{1}{3}} \right)^2} - \frac{1}{3} \geqslant - \frac{1}{3}\)所以 \(k < - \frac{1}{3}\).即 \(k\) 的取值范围是 \(\left( { - \infty , - \frac{1}{3}} \right)\) .

第353题

A.\(\frac {1} {4}\)

B.\(\frac {1} {2}\)

C.1

D.2

参考答案：B

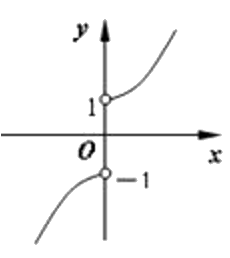
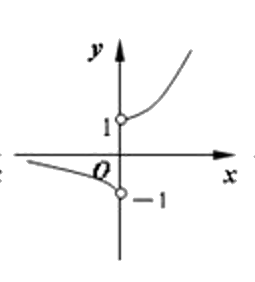
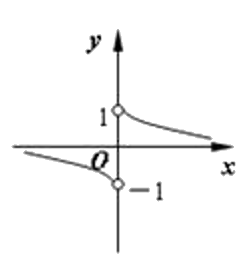
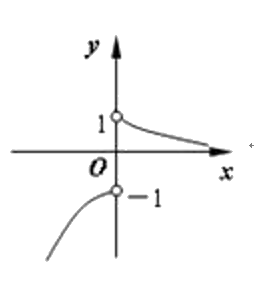
第354题

A.

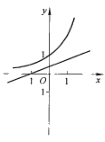
B.

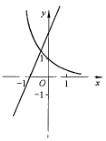
C.

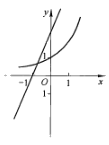
D.

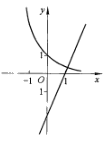
参考答案：C

第355题

A.\(\left( { - \infty , - 1} \right)\)

B.\(\left( { - 1,0} \right)\)

C.\(\left( {0,1} \right)\)

D.\(\left( {1, + \infty } \right)\)

参考答案：C

第356题

A.\(\left( { - 2,1} \right)\)

B.\(\left( { - 4,3} \right)\)

C.\(\left( { - 1,2} \right)\)

D.\(\left( { - 3,4} \right)\)

参考答案：C

第357题

A.\(x < y\)

B.\(x > y\)

C.\(x < - y\)

D.\(x > - y\)

参考答案：A

第358题

A.\(0\)

B.\(\frac{1}{2}\)

C.\( - \frac{1}{2}\)

D.\(1\)

参考答案：C

第359题

A.\(x + y > 0\)

B.\(x + y < 0\)

C.\(x - y > 0\)

D.\(x - y < 0\)

参考答案：A

第360题

A.\(\left( {0,4} \right)\)

B.\(\left( {0, + \infty } \right)\)

C.\(\left( {3,4} \right)\)

D.\(\left( {3, + \infty } \right)\)

参考答案：C