第281题

参考答案：由\(\mathrm{x}-1\ge 0\)得\( \mathrm{x}\ge 1\)，即函数定义域为\([1，+\infty )\)．因为函数\(y=2x\)与\( \mathrm{y}=\sqrt{x-1}\)在\([1，+\infty )\)上都是增函数，所以\(y=2x+\sqrt {x-1}\)在\([1，+\infty )\)上是增函数．所以当\(x=1\)时，\({y}_{\text{min}}=2\times 1+\sqrt {1-1}=2\)，即函数的最小值为2，没有最大值

第282题

参考答案：①\(∀{x}_{1}，{x}_{2}∈[1，2]\)，且\({x}_{1}<{x}_{2}\)，则\(f\left ( {{x}_{1}} \right )-f\left ( {{x}_{2}} \right )={x}_{1}-{x}_{2}+\frac {4} {{x}_{1}}-\frac {4} {{x}_{2}}=\left ( {{x}_{1}-{x}_{2}} \right )\left ( {1-\frac {4} {{x}_{1}{x}_{2}}} \right )=\frac {\left ( {{x}_{1}-{x}_{2}} \right )\left ( {{x}_{1}{x}_{2}-4} \right )} {{x}_{1}{x}_{2}}\).\( {\because x}_{1}<{x}_{2}\)， \( \therefore {x}_{1}-{x}_{2}<0\).

当\( 1\le {x}_{1}<{x}_{2}\le 2\)时，\( {x}_{1}{x}_{2}>0\)，\( 1<{x}_{1}{x}_{2}<4\)，即\( {x}_{1}{x}_{2}-4<0\).\( \mathrm{ }\therefore \mathrm{f}\left({x}_{1}\right)>f\left({x}_{2}\right)\)，即\(f(x)\)在区间\([1，2]\)上单调递减．

②由①知\(f(x)\)在区间\([1，2]\)上的最小值为\(f(2)\)，最大值为\(f(1)\)．\(∵f(1)=1+4=5\)，\(f\left ( {2} \right )=2+\frac {4} {2}=4\)，\(\therefore f(x)\)在区间\([1，2]\)上的最小值为4，最大值为5

第283题

参考答案：\( \left\{a\right|-5\le a\le 2\sqrt{2}-2\}\)

第284题

参考答案：\(f\left ( {x} \right )=a\left ( {{x}^{2}+2x} \right )+1=a\left ( {x+1} \right )^{2}-a+1\).

①若\(a<0\)，则当\(x=-1\)时，\(f\left ( {x} \right )_{\text{max}}=4\)，\(∴a=-3\).

②\(a>0\)若，则当\(x=2\)时，\(f\left ( {x} \right )_{\text{max}}=4\)，\(\therefore a=\frac {3} {8}\).

\(∴a\)的取值为\(-3\)或\( \frac{3}{8}\).

第285题

参考答案：当\(x∈[3，4]\)时，\(f(x)\)为增函数，最小值为\(f(3)=-7\)，最大值为\(f(4)=-4\).

第286题

参考答案：\( f\left(x\right)={\left(x-2\right)}^{2}-8\)在\([-3，2]\)上是减函数，在\([2，4]\)上是增函数，\(∴\)最小值为\(f(2)=-8\)

又\(f(-3)=17\)，\(f(4)=-4\)，(也可以通过比较\(-3\)和4与对称轴\(x=2\)的距离，抛物线开口向上时，哪一个距离对称轴远哪一个对应的函数值就较大，抛物线开口向下时，哪一个距离对称轴近哪一个对应的函数值就较大)

\(∴\)最大值为17.

第287题

参考答案：令\( \sqrt{x+1}=t\)，则\( \mathrm{x}={t}^{2}-1\left(t\ge 0\right)\)，所以\( \mathrm{y}={t}^{2}-t-1\left(t\ge 0\right)\)．又\( \mathrm{y}={t}^{2}-t-1\)在\( \left[0，\frac{1}{2}\right]\)上单调递减，在\( [\frac{1}{2}，+\mathrm{\infty })\)上单调递增，所以\({y}_{\text{min}}=\left ( {\frac {1} {2}} \right )^{2}-\frac {1} {2}-1=-\frac {5} {4}\)，无最大值．

故函数\( y=x-\sqrt{x+1}\)的最小值为\( -\frac{5}{4}\)，无最大值

第288题

参考答案：\( y=\frac{{x}^{2}+8}{x-1}=\frac{{x}^{2}-1+9}{x-1}=\left(x+1\right)+\frac{9}{x-1}=\left(x-1\right)+\frac{9}{x-1}+2\).

\(∵x>1\)，\(∴x-1>0\)，\(\therefore \left ( {x-1} \right )+\frac {9} {x-1}+2\ge 2\sqrt {\left ( {x-1} \right )\cdot \frac {9} {x-1}}+2=8\).当且仅当\( x-1=\frac{9}{x-1}\)，即\(x=4\)时等号成立．\(∴y\)有最小值8.

第289题

参考答案：\( \left\{-1，\frac{1}{2}，1，3\right\}\)

第290题

参考答案：令\(f(x) = {x^{\frac{5}{3}}} = \sqrt[3]{{{x^5}}}\)，定义域为\(\operatorname{R} \)，因为\(f( - x) = - \sqrt[3]{{{x^5}}} = - f(x)\)，所以函数\(f\left ( {x} \right )\)为奇函数，且在\((0, + \infty )\)上单调递增，所以\(f\left ( {x} \right )\)在\(\operatorname{R} \)上单调递增，故值域为\(\operatorname{R} \).

令\(g(x) = {x^{\frac{1}{5}}} = \sqrt[5]{x}\)，定义域为\(\operatorname{R} \)，因为\(g( - x) = - \sqrt[5]{x} = - g(x)\)，所以函数\(g(x)\)为奇函数，且在\((0, + \infty )\)上单调递增，所以\(g(x)\)在\(\operatorname{R} \)上单调递增，故值域为\(\operatorname{R} \).

第291题

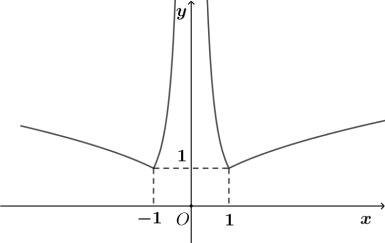
A.

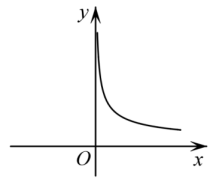
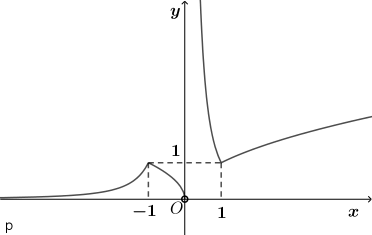
B.

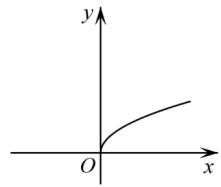
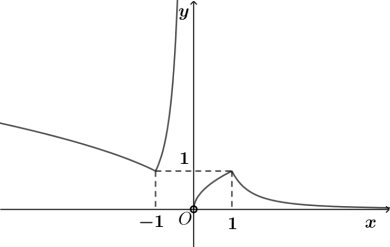
C.

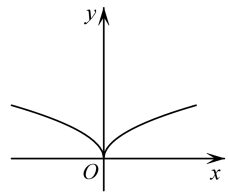
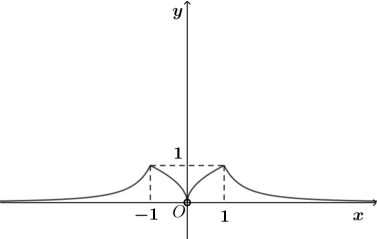
D.

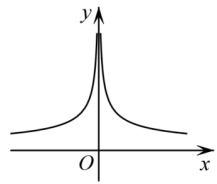
参考答案：A

第292题

A.1

B.2

C.3

D.4

参考答案：A

第293题

A.

B.

C.

D.

参考答案：A

第294题

A.①②④⑤

B.③④⑥

C.①②⑥

D.①②④⑤⑥

参考答案：C

第295题

A.恒大于0

B.恒小于0

C.等于0

D.无法判断

参考答案：A

第296题

A.\(b < c < a\)

B.\(a < c < b\)

C.\(b < a < c\)

D.\(c < b < a\)

参考答案：A

第297题

参考答案：由题意，函数\(f\left( x \right) = {x^{4m - {m^2}}}\)（\(m \in Z\)）的图像关于\(y\)轴对称，且\(f\left( 2 \right) < f\left( 3 \right)\)，所以在区间\((0, + \infty )\)为单调递增函数，所以\({m^2} - 4m < 0\)，解得\(0 < m < 4\)，由\(m \in Z\)，\(m = 1,2,3\)。又函数\(f\left( x \right) = {x^{4m - {m^2}}}\)的图像关于\(y\)轴对称，所以\(4m - {m^2}\)为偶数，所以\(m = 2\)，所以\(f\left( x \right) = {x^4}\).

第298题

参考答案：因为函数\(f\left( x \right) = {x^4}\)图象关于\(y\)轴对称，且在区间\((0, + \infty )\)为单调递增函数，

所以不等式\(f\left( {a + 2} \right) < f\left( {1 - 2a} \right)\)，等价于\(|a + 2| < |1 - 2a|\)，

解得\(a>3\)或\(a < - \frac{1}{3}\)，

所以实数\(a\)的取值范围是\(( - \infty , - \frac{1}{3}) \cup (3, + \infty )\).

第299题

参考答案：因为\(f\left ( {x} \right )={x}^{-\frac {1} {2}}\)的定义域为\((0，+∞)\)，且在\((0，+∞)\)上单调递减，所以\(\left \{ \begin{gathered} {a+1>0} \\ {3-2a>0} \\ {a+1>3-2a} \end{gathered} \right .\)

得\(\frac {2} {3}<a<\frac {3} {2}\)

第300题

A.\(f(a)<f(b)<f\left ( {\frac {1} {a}} \right )<f\left ( {\frac {1} {b}} \right )\)

B.\(f\left ( {\frac {1} {a}} \right )<f\left ( {\frac {1} {b}} \right )<f(b)<f(a)\)

C.\(f(a)<f(b)<f\left ( {\frac {1} {b}} \right )<f\left ( {\frac {1} {a}} \right )\)

D.\(f\left ( {\frac {1} {a}} \right )<f(a)<f\left ( {\frac {1} {b}} \right )<f(b)\)

参考答案：C