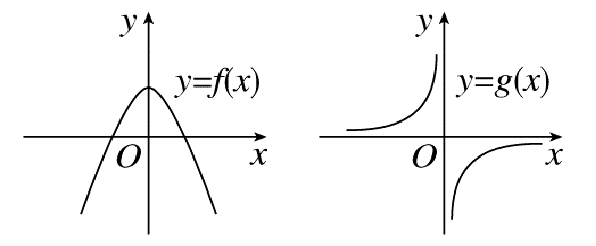“微信扫一扫”进入考试题库练习及模拟考试
高中数学必修 第一册(648题)
参考答案:\(-1\)
参考答案:\(-2020\)
第223题
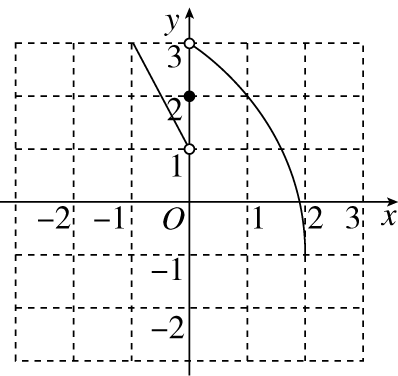
求这个二次函数的解析式;
参考答案:设二次函数的解析式为\(y=a{(x-6)}^{2}+5(a<0)\).
将点\(A(0,2)\)代入\(y=a{(x-6)}^{2}+5\),可得\(a{(0-6)}^{2}+5=2\),\(\therefore a=-\frac {1} {12}\),\(\therefore y=-\frac {1} {12}\left ( {x-6} \right )^{2}+5\).
第224题
该同学能把铅球掷出去多远(结果精确到0.01 m,
参考答案:令\(y=0\),得\(-\frac {1} {12}\left ( {x-6} \right )^{2}+5=0\),
解得\(x=6+2\sqrt {15}\)或\(x=6-2\sqrt {15}\) (舍去).
又\( 6+2\sqrt{15}\approx 6+2\times 3.873=13.746\approx 13.75\),
\(∴\)该同学能把铅球掷出去约13.75m
A.先向左平移3个单位长度,再向上平移1个单位长度
B.先向右平移3个单位长度,再向上平移1个单位长度
C.先向右平移3个单位长度,再向下平移1个单位长度
D.先向左平移3个单位长度,再向下平移1个单位长度
参考答案:C
第226题
一水池有2个进水口,1个出水口,每个进水口的进水速度如图甲所示,出水口的出水速度如图乙所示.某天从0 h到6 h,该水池的蓄水量如图丙所示,则下列说法正确的是( )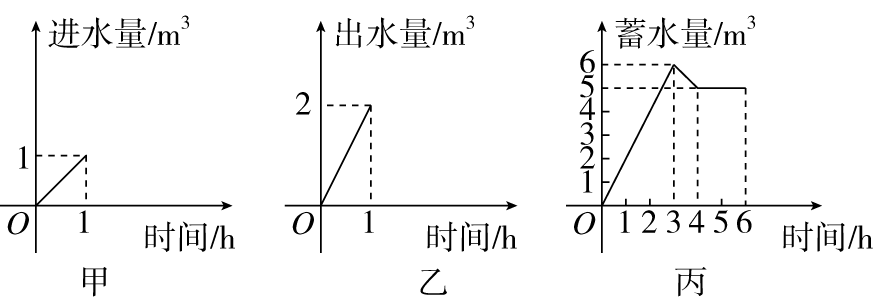
A.0 h到3 h只进水不出水
B.3 h到4 h不进水只出水
C.3 h到4 h有一个进水口关闭
D.4 h到6 h不进水不出水
参考答案:AC
A.\(f(2020)=0\)
B.方程\(f\left ( {x} \right )=\frac {1} {4}x-1\)有三个实数根
C.当\(x∈[4,6)\)时,\(f(x)=|x-5|-1\)
D.若函数\(y=f(x)-t\)在\((-∞,6)\)上有8个零点\( {x}-{i}\)(i=1,2,3,…,8),则\({x}-{1}f\left ( {{x}-{1}} \right )+{x}-{2}f\left ( {{x}-{2}} \right )+\cdots +{x}-{8}f\left ( {{x}-{8}} \right )\)的取值范围为\((-16,0)\)
参考答案:ACD
第228题
如图所示,函数图象由两条射线及抛物线的一部分组成,则函数的解析式为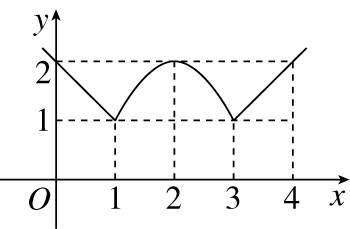
参考答案:\(\left \{ \begin{gathered} {-x+2,x<1} \\ {-{x}^{2}+4x-2,1\leq x\leq 3} \\ {x-2,x>3} \end{gathered} \right .\)
A.

B.
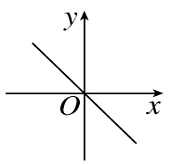
C.
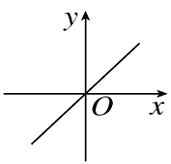
D.
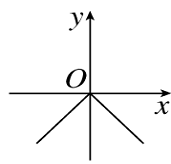
参考答案:C
第233题
求
参考答案:\(f({a}^{2}+1)=3-{({a}^{2}+1)}^{2}=-{a}^{4}-2{a}^{2}+2\),\(f(f(3))=f(-6)=13\).
第234题
当
参考答案:当\(x>0\)时,\({3-x}^{2}\ge 2\),解得\(0<x≤1\);
当\(x=0\)时,\(f(x)=2\),满足题意;
当\(x<0\)时,\(1-2x≥2\),解得\(x\le -\frac {1} {2}\).
综上,当\(f(x)≥2\)时,\(x\)的取值范围为\(\left \{ {x|x\le -\frac {1} {2}或0\leq x\leq 1} \right \} \).
A.

B.
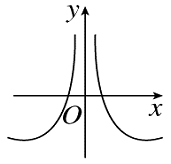
C.
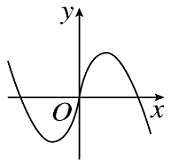
D.
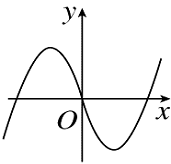
参考答案:A
第236题
已知函数
A.\(\left [ {-8,16} \right ]\)
B.\((-\infty ,-8]\cup [16,+\infty )\)
C.\((-\infty ,-8]\cup [16,+\infty )\)
D.\([16,+\infty )\)
参考答案:B
A.\(\left ( {-\infty ,\frac {1} {2}} \right )\)
B.\(\left ( {\frac {1} {2},+\infty } \right )\)
C.\((-\infty ,\frac {1} {2}]\)
D.\([\frac {1} {2},+\infty )\)
参考答案:D
A.\((-∞,1]\)
B.\((0,1]\)
C.\(\left ( {0,+∞} \right )\)
D.\([1,+∞)\)
参考答案:B
参考答案:\( [\frac{3}{5}, 3)\)
第240题
求证:函数
参考答案:\(∀{x}_{1},{x}_{2}∈(0,1)\),且\({x}_{1}<{x}_{2}\),则
\(f\left ( {{x}_{1}} \right )-f\left ( {{x}_{2}} \right )=\left ( {{x}_{1}+\frac {1} {{x}_{1}}} \right )-\left ( {{x}_{2}+\frac {1} {{x}_{2}}} \right )=\left ( {{x}_{1}-{x}_{2}} \right )+\left ( {\frac {1} {{x}_{1}}-\frac {1} {{x}_{2}}} \right )=\left ( {{x}_{1}-{x}_{2}} \right )+\frac {{x}_{2}-{x}_{1}} {{x}_{1}{x}_{2}}=\left ( {{x}_{1}-{x}_{2}} \right )\cdot \frac {{{x}_{1}x}_{2}-1} {{x}_{1}{x}_{2}}\)
\(∵0<{x}_{1}<{x}_{2}<1,∴{x}_{1}-{x}_{2}<0,0<{x}_{1}{x}_{2}<1,{x}_{1}{x}_{2}-1<0\),\(\therefore f\left ( {{x}_{1}} \right )-f\left ( {{x}_{2}} \right )>0\)即\(f\left ( {{x}_{1}} \right )>f\left ( {{x}_{2}} \right )\).\(∴f(x)\)在\((0,1)\)上单调递减.