高中数学必修 第一册

第181题

参考答案：\((\frac {25} {9}，\frac {49} {16}]\)

第182题

参考答案：\(m < - 2\)

第183题

参考答案：\( - 2 < m < - 1\)

第184题

A.\( -\frac{3}{4}\)

B.\( \frac{3}{4}\)

C.\( -\frac{3}{5}\)

D.\( \frac{3}{5}\)

参考答案：A

第185题

A.\( \pm 1\)

B.\( -1\)

C.\( -2\)或\( -1\)

D.\( \pm 1\)或\( -2\)

参考答案：B

第186题

函数\(f\left ( {x} \right )\)与\(g\left ( {x} \right )\)的对应关系如下表．

A.0

B.3

C.1

D.\(-1\)

参考答案：A

第187题

参考答案：\( {e}^{2}+1\)

第188题

参考答案：3

第189题

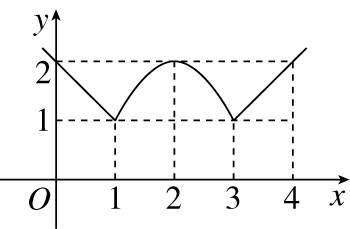
参考答案：\(f\left ( {x} \right )=\left \{ \begin{gathered} {-x+2，x<1} \\ {-{x}^{2}+4x-2，1\leq x\leq 3} \\ {x-2，x>3} \end{gathered} \right .\)

第190题

参考答案：∵\( {a}^{2}+2\ge 2\)，\(\therefore f\left ( {{a}^{2}+2} \right )=2\left ( {{a}^{2}+2} \right )\)，

∴\( 2\left({a}^{2}+2\right)\ge a+4\)，

∴\( 2{a}^{2}-a\ge 0\)，

\(\therefore a\le 0\)或\(a\ge \frac {1} {2}\).

\(\therefore a\)的取值范围为\((-∞，0]\cup [\frac {1} {2}，+\infty )\).

第191题

参考答案：∵\(-\pi <-1\)，\(∴f(-π)=-π+2\).

∵\( -1<\frac{3}{2}<2\)，\(\therefore f\left ( {\frac {3} {2}} \right )=\left ( {\frac {3} {2}} \right )^{2}=\frac {9} {4}>2\).

\(\therefore f\left ( {f\left ( {\frac {3} {2}} \right )} \right )=f\left ( {\frac {9} {4}} \right )=2\times \frac {9} {4}=\frac {9} {2}\).

第192题

参考答案：\(y=\left \{ \begin{gathered} {0，(0<x\leq 800)} \\ {0.14(x-800)，(800<x\leq 4000)} \\ {0.1x，(x>4000)} \end{gathered} \right .\)

第193题

参考答案：令\(0.14(x-800)=660\)，得\( \mathrm{x}=\frac{38600}{7}\approx 5514.29\notin (800，4000]\)．

令\(0.11x=660\)，得\(x=6000∈(4000，+∞)\)．故这个人的稿费是6000元．

第194题

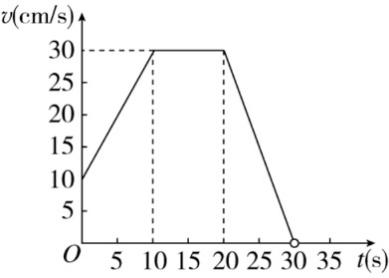
参考答案：\( \mathrm{v}\left(\mathrm{t}\right)=\left\{\begin{array}{c}2t+10，t\in [0，10)\\ 30，t\in [10，20)\\ -3t+90，t\in [20，30)\end{array}\right.\)

当\(t=9\)时，\(v(9)=2×9+10=28(\text{cm/s})\)．

第195题

A.

B.

C.

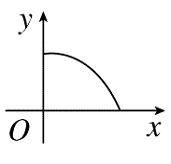
D.

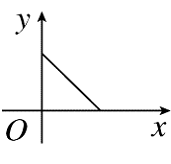
参考答案：C

第196题

参考答案：\(\left[ { - 5, - \frac{{3\pi }}{2}} \right) \cup \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right) \cup \left( {\frac{{3\pi }}{2},5} \right]\)

第197题

参考答案：4

第198题

参考答案：②

第199题

参考答案：16

第200题

参考答案：\(\left[ { - 1,\frac{3}{2}} \right]\)