第261题

参考答案：\(x\left( {x - 1} \right)\)

第262题

参考答案：\( - 4\)

第263题

参考答案：证明：函数\(f\left( x \right)\)的定义域为\({\mathbf{R}}\)，关于原点对称，因为函数\(f\left( x \right)\)对任意\(x,\;\;y \in {\mathbf{R}}\)，都有\(f\left( {x + y} \right) = f\left( x \right) + f\left( y \right)\)，令\(x = y = 0\)，则\(f\left( 0 \right) = 2f\left( 0 \right)\)，得\(f\left( 0 \right) = 0\)，令\(y = - x\)，则\(f\left( 0 \right) = f\left( x \right) + f\left( { - x} \right)\)，所以\(f\left( x \right) + f\left( { - x} \right) = 0\)，即\(f\left( { - x} \right) = - f\left( x \right)\)，所以\(f\left( x \right)\)为奇函数．

第264题

参考答案：奇函数

\(f\left( x \right)\)的定义域是\(\left( { - \infty ,0} \right) \cup \left( {0, + \infty } \right)\)，关于原点对称，

又\(f\left( { - x} \right) = {\left( { - x} \right)^3} - \frac{1}{{ - x}} = - \left( {{x^3} - \frac{1}{x}} \right) = - f\left( x \right)\)，所以\(f\left( x \right)\)是奇函数．

第265题

参考答案：既不是奇函数也不是偶函数

因为\(f\left( x \right)\)的定义域为\(\left[ { - 1,1} \right)\)，不关于原点对称，

所以\(f\left( x \right)\)既不是奇函数也不是偶函数．

第266题

参考答案：既是奇函数又是偶函数

因为\(f\left( x \right)\)的定义域为\(\left\{ { - \sqrt 3 ,\sqrt 3 } \right\}\)，所以\(f\left( x \right) = 0\)，

则\(f\left( x \right)\)既是奇函数又是偶函数．

第267题

参考答案：

 偶函数

方法一（定义法）   因为函数\(f\left( x \right)\)的定义域为R，所以函数\(f\left( x \right)\)的定义域关于原点对称．

①当x＞1时，\( - x < - 1\)，所以\(f\left( { - x} \right) = \left( { - 2} \right) \times \left( { - x} \right) = 2x = f\left( x \right)\)；

②当\( - 1 \leqslant x \leqslant 1\)时，\(f\left( x \right) = 2\)；

③当\(x < - 1\)时，\( - x > 1\)，所以\(f\left( { - x} \right) = 2 \times \left( { - x} \right) = - 2x = f\left( x \right)\)．

综上，可知函数\(f\left( x \right)\)为偶函数．

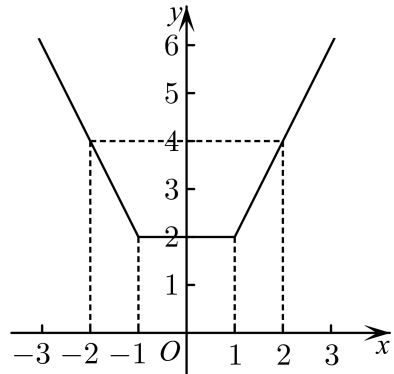
方法二（图象法）   作出函数\(f\left( x \right)\)的图象，如图所示，易知函数\(f\left( x \right)\)为偶函数．

第268题

A.\(\left( {3, + \infty } \right)\)

B.\(\left( { - \infty , - 1} \right) \cup \left( {0,3} \right)\)

C.\(\left( { - 1, + \infty } \right)\)

D.\(\left( { - 3,0} \right) \cup \left( {1, + \infty } \right)\)

参考答案：B

第269题

A.\(f\left( x \right)\)的图象关于直线\(x = 1\)对称

B.\(f\left( x \right)\)在\(\left[ {0,1} \right]\)上是增函数

C.\(f\left( x \right)\)在\(\left[ {1,2} \right]\)上是减函数

D.\(f\left( 2 \right) = f\left( 0 \right)\)

参考答案：AD

第270题

A.\(f\left( x \right)\)的图象关于直线\(x=-1\)对称

B.\(f\left( x \right)\)在\(( - 1, + \infty )\)上为增函数

C.\(f\left( 1 \right) = f\left( { - 2} \right)\)

D.\(f\left( { - 3} \right) < f\left( 0 \right) < f\left( { - \frac{1}{2}} \right)\)

参考答案：AD

第271题

A.\(\left( {1,\frac{5}{3}} \right)\)

B.\(\left( { - \infty ,1} \right) \cup \left( {\frac{5}{3}, + \infty } \right)\)

C.\(\left( { - \infty ,1} \right)\)

D.\(\left( {1, + \infty } \right)\)

参考答案：B

第272题

参考答案：\(\sin \pi x\)（答案不唯一）

第273题

A.\(f\left( {16} \right) < f\left( { - 17} \right) < f\left( {18} \right)\)

B.\(f\left( {18} \right) < f\left( {16} \right) < f\left( { - 17} \right)\)

C.\(f\left( {16} \right) < f\left( {18} \right) < f\left( { - 17} \right)\)

D.\(f\left( { - 17} \right) < f\left( {16} \right) < f\left( {18} \right)\)

参考答案：D

第274题

A.\(f\left( x \right)\)是偶函数

B.\(f\left( x \right)\)是周期函数

C.\(f\left( {\frac{{99}}{2}} \right) = - 1\)

D.\(x \in \left[ { - 1,0} \right)\)时，\(f\left( x \right) = x\)

参考答案：AB

第275题

A.\( - 1\)

B.\( - 2\)

C.0

D.2

参考答案：A

第276题

A.0

B.1

C.\(-1\)

D.\(\frac{1}{2}\)

参考答案：B

第277题

参考答案：\( - 1\)

第278题

A.\(f\left( x \right)\)为奇函数

B.\(f\left( x \right)\)周期为2

C.\(f\left( {\frac{9}{2}} \right) = 1\)

D.\(f\left( {x - 2} \right)\)是奇函数

参考答案：AD

第279题

参考答案：4

第280题

A.\(f\left ( {x} \right )\)为周期函数

B.\(f\left ( {x} \right )\)为\({\rm{R}}\)上的偶函数

C.\(f\left ( {x} \right )\)为\({\rm{R}}\)上的单调函数

D.\(f\left ( {x} \right )\)的图象关于点\(\left( { - \frac{3}{4},0} \right)\)对称

参考答案：ABD