
“微信扫一扫”进入题库练习及模拟考试
高中数学必修 第一册(648题)
判断下列函数的奇偶性.
{ - 2x,x < - 1} \\
{2, - 1 \leqslant x \leqslant 1} \\
{2x,x > 1}
\end{array}} \right.\)
知识点:第三章 函数的概念与性质
参考答案:
偶函数
方法一(定义法) 因为函数
①当x>1时,
②当
③当
综上,可知函数
方法二(图象法) 作出函数
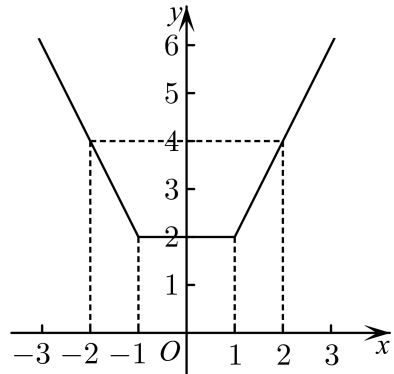

“微信扫一扫”进入题库练习及模拟考试
判断下列函数的奇偶性.
{ - 2x,x < - 1} \\
{2, - 1 \leqslant x \leqslant 1} \\
{2x,x > 1}
\end{array}} \right.\)
参考答案:
偶函数
方法一(定义法) 因为函数
①当x>1时,
②当
③当
综上,可知函数
方法二(图象法) 作出函数
