
“微信扫一扫”进入考试题库练习及模拟考试
高中数学必修 第一册(648题)
第321题
参考答案:\(\sqrt[6]{{8\sqrt 2 }} = \sqrt[6]{{{2^3} \cdot {2^{\frac{1}{2}}}}} = {({2^{\frac{7}{2}}})^{\frac{1}{6}}} = {2^{\frac{7}{{12}}}};\)
第322题
参考答案:\(\sqrt {a\sqrt a } = \sqrt {a \cdot {a^{\frac{1}{2}}}} = \sqrt {{a^{\frac{3}{2}}}} = {({a^{\frac{3}{2}}})^{\frac{1}{2}}} = {a^{\frac{3}{4}}};\)
第323题
参考答案:\({b^3} \cdot \sqrt[3]{{{b^2}}} = {b^3} \cdot {b^{\frac{2}{3}}} = {b^{\frac{{11}}{3}}};\)
第324题
参考答案:\(\frac{1}{{\sqrt[3]{{x{{(\sqrt[5]{{{x^2}}})}^2}}}}} = \frac{1}{{\sqrt[3]{{x \cdot {{({x^{\frac{2}{5}}})}^2}}}}} = \frac{1}{{\sqrt[3]{{x \cdot {x^{\frac{4}{5}}}}}}} = \frac{1}{{\sqrt[3]{{{x^{\frac{9}{5}}}}}}} = \frac{1}{{{{({x^{\frac{9}{5}}})}^{\frac{1}{3}}}}} = \frac{1}{{{x^{\frac{3}{5}}}}} = {x^{ - \frac{3}{5}}}.\)
参考答案:
(1)原式= 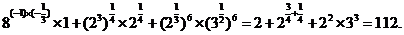
(2)
第326题
参考答案:法一:\(\sqrt {\frac {3-2\sqrt {2}} {3+2\sqrt {2}}}=\sqrt {\frac {\left ( {\sqrt {2}-1} \right )^{2}} {\left ( {\sqrt {2}+1} \right )^{2}}}=\frac {\sqrt {2}-1} {\sqrt {2}+1}=\frac {\left ( {\sqrt {2}-1} \right )^{2}} {\left ( {\sqrt {2}+1} \right )\left ( {\sqrt {2}-1} \right )}=3-2\sqrt {2}\)
法二:\(\sqrt {\frac {3-2\sqrt {2}} {3+2\sqrt {2}}}=\sqrt {\frac {\left ( {3-2\sqrt {2}} \right )^{2}} {\left ( {3+2\sqrt {2}} \right )\left ( {3-2\sqrt {2}} \right )}}=3-2\sqrt {2}\)
参考答案:∵\(\sqrt[{3}] {\left ( {-6} \right )^{3}}=-6,\sqrt[{4}] {\left ( {\sqrt {5}-4} \right )^{4}}=\left | {\sqrt {5}-4} \right |=4-\sqrt {5},\sqrt[{3}] {\left ( {\sqrt {5}-4} \right )^{3}}=\sqrt {5}-4\) ,
∴原式\(-6+4-\sqrt {5}+\sqrt {5}-4=6\) .
第328题
参考答案:原式 \( = \sqrt {{{(\sqrt 3 )}^2} + 2\sqrt 6 + {{(\sqrt 2 )}^2}} + \sqrt {{{(\sqrt 3 )}^2} - 2\sqrt 6 + {{(\sqrt 2 )}^2}} \)\( = \sqrt {{{(\sqrt 3 + \sqrt 2 )}^2}} + \sqrt {{{(\sqrt 3 - \sqrt 2 )}^2}} = |\sqrt 3 + \sqrt 2 | + |\sqrt 3 - \sqrt 2 |\)\( = \sqrt 3 + \sqrt 2 + \sqrt 3 - \sqrt 2 = 2\sqrt 3 \).
参考答案:\({3^{\frac{1}{4}}}\);\(9\sqrt 5 .\)
第330题
参考答案:原式= \({[{(0.3)^3}]^{\tfrac{2}{3}}} + {[{(\frac{3}{5})^3}]^{ - \tfrac{1}{3}}} - {[{(\frac{5}{3})^2}]^{0.5}}\)
= \({(0.3)^2} + {(\frac{3}{5})^{ - 1}} - \frac{5}{3}\)
= \(\frac{9}{{100}} + \frac{5}{3} - \frac{5}{3}\)
= \(\frac{9}{{100}}\)
参考答案:原式=\(\left ( {-2{a}^{\frac {1} {3}}{b}^{-\frac {3} {4}}} \right )\cdot {a}^{3}{b}^{-2}\div 4{a}^{\frac {10} {3}}{b}^{-\frac {11} {4}}
=\left [ {\left ( {-2} \right )\div 4} \right ]{\cdot a}^{\frac {1} {3}+3-\frac {10} {3}}\cdot {b}^{-\frac {3} {4}-2+\frac {11} {4}}
=-\frac {1} {2}\)
A.\(\frac{1}{{{6^4}}}\)
B.\({2^{2n + 5}}\)
C.\({2^{{n^2} - 2n + 6}}\)
D.\({\left( {\frac{1}{2}} \right)^{2n - 7}}\)
参考答案:D
参考答案:\(\frac{1}{{2(1 - {2^{ - \tfrac{1}{{32}}}})}}\)
第334题
①
参考答案:①\(\because {({a^{\tfrac{1}{2}}} + {a^{ - \tfrac{1}{2}}})^2} = 9\)
\(\therefore a + {a^{ - 1}} + 2 = 9\)
\(\therefore a + {a^{ - 1}} = 7\)
第335题
②
参考答案:②\(\because {(a + {a^{ - 1}})^2} = {a^2} + {a^{ - 2}} + 2 = 49\)\(\therefore {a^2} + {a^{ - 2}} = 47\)
第336题
③
参考答案:③原式= \(\frac {\left ( {{a}^{\frac {1} {2}}-{a}^{-\frac {1} {2}}} \right )\left ( {a+{a}^{\frac {1} {2}}\cdot {a}^{-\frac {1} {2}}+{a}^{-1}} \right )} {{a}^{\frac {1} {2}}-{a}^{-\frac {1} {2}}}\)
= \(a + {a^{ - 1}} + 1\)
= \(7 + 1\)
= \(8\)
参考答案:8;1
A.\(\left( {1, + \infty } \right)\)
B.\(\left( {1,8} \right)\)
C.\(\left( {4,8} \right)\)
D.\(\left[ {4,8} \right)\)
参考答案:D
第339题
已知关于
A.\(\left( { - \infty ,0} \right)\)
B.\(\left( {1,2} \right)\)
C.\(\left( {0, + \infty } \right)\)
D.\(\left( {0,1} \right)\)
参考答案:D
A.\(( - 2, - 1)\)
B.\(( - 2, + \infty )\)
C.\(\left( { - \infty , - 1} \right]\)
D.\(\left( { - 2, - 1} \right]\)
参考答案:D