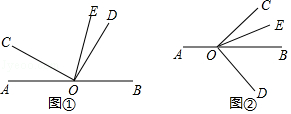第101题

已知关于x的方程2x+8＝﹣6与方程2x﹣3a＝﹣5的解相同，则a的值为（　　）

A.13

B.3

C.﹣3

D.8

参考答案：C

解析：

【分析】先解方程2x+8＝﹣6得x＝﹣7，根据同解方程的定义把x＝﹣7代入2x﹣3a＝﹣5得﹣14﹣3a＝﹣5，然后解关于a的一元一次方程即可．

【解答】解：∵2x+8＝﹣6，

∴x＝﹣7，

把x＝﹣7代入2x﹣3a＝﹣5得﹣14﹣3a＝﹣5，

∴a＝﹣3．

故选：C．

第102题

有一道题目是一个多项式A减去多项式2x²+5x﹣3，小胡同学将2x²+5x﹣3抄成了2x²+5x+3，计算结果是﹣x²+3x﹣7，这道题目的正确结果是（　　）

A.x²+8x﹣4

B.﹣x²+3x﹣1

C.﹣3x²﹣x﹣7

D.x²+3x﹣7

参考答案：B

解析：

【分析】直接利用整式的加减运算法则得出A，进而利用整式的加减运算法则得出这道题目的正确结果．

【解答】解：由题意可得：A﹣（2x²+5x+3）＝﹣x²+3x﹣7，

则A＝﹣x²+3x﹣7+2x²+5x+3

＝x²+8x﹣4，

故这道题目的正确结果是：x²+8x﹣4﹣（2x²+5x﹣3）

＝x²+8x﹣4﹣2x²﹣5x+3

＝﹣x²+3x﹣1．

故选：B．

第103题

已知有理数a，b在数轴上表示的点如图所示，化简|b﹣a|﹣|a+2b|+|﹣a﹣b|＝（　　）

A.a

B.﹣a﹣4b

C.3a+2b

D.a﹣2b

参考答案：A

解析：

【分析】结合数轴知b＜﹣1＜0＜a＜1，据此判断出b﹣a＜0，a+2b＜0，﹣a﹣b＞0，再利用绝对值的性质去绝对值符号、合并即可得出答案．

【解答】解：由数轴知b＜﹣1＜0＜a＜1，

∴b﹣a＜0，a+2b＜0，﹣a﹣b＞0，

则原式＝a﹣b+a+2b﹣a﹣b

＝a，

故选：A．

第104题

如图，是一个正方体的平面展开图，标有字母A的面为正方体的正面，如果正方体两个面上标注的代数式的值分别与相对面上的数字相等，在求x、y的值时，所列方程正确的是（　　）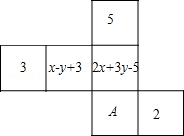

A.

B.

C.

D.

参考答案：D

解析：

【分析】根据正方体的相对的两个面上标注的代数式的值与相对面上的数字相等，可得出方程组．

【解答】解：根据题意得：．

故选：D．

第105题

我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺．则符合题意的方程是（　　）

A.x＝（x﹣5）﹣5

B.x＝（x+5）+5

C.2x＝（x﹣5）﹣5

D.2x＝（x+5）+5

参考答案：A

解析：

【分析】设绳索长x尺，则竿长（x﹣5）尺，根据“将绳索对半折后再去量竿，就比竿短5尺”，即可得出关于x的一元一次方程，此题得解．

【解答】解：设绳索长x尺，则竿长（x﹣5）尺，

依题意，得：x＝（x﹣5）﹣5．故选：A．

第106题

已知点A，B，C在同一直线上，若AB＝20cm，AC＝30cm，点M、N分别是线段AB、AC中点，求线段MN的长是（　　）

A.5cm

B.5cm或15cm

C.25cm

D.5cm或25cm

参考答案：D

解析：

【分析】题中没有指明点C的具体位置故应该分两种情况进行分析，从而求得线段NM的长．

【解答】解：（1）当点C位于点B的右边时，MN＝（AC﹣AB）＝5cm，

（2）当点C位于点A的左边时，MN＝（AC+AB）＝25cm

故线段MN的长为5cm或25cm．

故选：D．

第107题

如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下列沿顺时针方向跳两个点：若停在偶数点上，则下次沿逆时针方向跳一个点，若青蛙从1这点开始跳，则经过2020次后它停在哪个数对应的点上（　　）

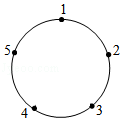
A.1

B.2

C.3

D.5

参考答案：A

解析：

【分析】分别得到从2开始起跳后落在哪个点上，得到相应的规律，看2020次跳后应循环在哪个数上即可．

【解答】解：第1次跳后落在3上；

第2次跳后落在5上；

第3次跳后落在2上；

第4次跳后落在1上；

…

4次跳后一个循环，依次在1，3，5，2这4个数上循环，

∵2020÷4＝505，

∴应落在1上．

故选：A．

第108题

定义了一种新运算“*”，规则如下：a*b＝ab﹣a²，则（﹣3）*2＝　　．

参考答案：﹣15

解析：

【分析】原式利用题中的新定义计算即可求出值．

【解答】解：根据题中的新定义得：原式＝（﹣3）×2﹣（﹣3）²＝﹣6﹣9＝﹣15．

故答案为：﹣15．

第109题

已知关于x的多项式﹣2x⁵﹣ax⁴+3x⁴﹣bx³+2x³+5x²+1合并同类项后缺少四次项和三次项，且y＜﹣2，则|y﹣a|﹣|y+b|﹣|a﹣2b|＝　　．

参考答案：4

解析：

【分析】根据多项式的概念以及合并同类项法则即可求出a，b的值，再根据绝对值的性质解答即可．

【解答】解：﹣2x⁵﹣ax⁴+3x⁴﹣bx³+2x³+5x²+1

＝﹣2x⁵+（3﹣a）x⁴+（2﹣b）x³+5x²+1，

∵关于x的多项式﹣2x⁵﹣ax⁴+3x⁴﹣bx³+2x³+5x²+1合并同类项后缺少四次项和三次项，

∴3﹣a＝0，2﹣b＝0，

解得a＝3，b＝2，

∵y＜﹣2，

∴y﹣a＜0，y+b＜0，

∴|y﹣a|﹣|y+b|﹣|a﹣2b|

＝a﹣y﹣（﹣y﹣b）﹣|3﹣4|

＝3﹣y+y+2﹣1

＝4．

故答案为：4．

第110题

如图，点A，B是直线l上的两点，点C，D在直线l上且点C在点D的左侧，点D在点B的右侧．AC：CB＝1：2，BD：AB＝2：3．若CD＝12，则AB＝　　．

参考答案：4.5或9

解析：

【分析】根据两点间的距离的性质和已知条件，分情况讨论C点的位置即可求解．

【解答】解：对C点的位置分情况讨论如下：

①C点在A点的左边，

∵AC：CB＝1：2，BD：AB＝2：3，

假设AC＝3k，

则AB＝3k，BD＝2k，

∴CD＝3k+3k+2k＝8k，

∵CD＝12，

∴k＝1.5，

∴AB＝4.5；

②C点在线段AB上，

∵AC：CB＝1：2，BD：AB＝2：3，

假设AC＝k，

则CB＝2k，BD＝2k，

∴CD＝CB+BD＝4k，

∵CD＝12，

∴k＝3，

∴AB＝AC+CB＝3k＝9；

③C点在B点后，不符合题意，舍去；

∴综上所述，AB＝4.5或9．

第111题

如图，都是由同样大小的黑棋子按一定规律摆出的图案，第①个图案有4个黑棋子．第②个图案有9个黑棋子，第③个图案有14个黑棋子，依次规律，第n个图案有199个黑棋子，则n＝　　．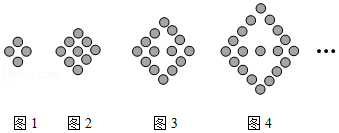

参考答案：40

解析：

【分析】设第m（m为正整数）个图案有a_m个黑棋子，根据各图形中黑色棋子个数的变化，即可找出变化规律“a_m＝5m﹣1（m为正整数）”，代入a_n＝199求出与之对应的n值即可得出结论．

【解答】解：设第m（m为正整数）个图案有a_m个黑棋子．

观察图形，可知：a₁＝4，a₂＝9，a₃＝14，a₄＝19，

∴a₂﹣a₁＝5，a₃﹣a₂＝5，a₄﹣a₃＝5，

∴a_m﹣a_m﹣1＝5，

∴a_m＝a₁+（a₂﹣a₁）+…+（a_m﹣a_m﹣1）＝4+5（m﹣1）＝5m﹣1．

当a_n＝199时，5n﹣1＝199，

∴n＝40．

故答案为：40．

第112题

（1）计算：（﹣）⁴×÷×（﹣2）³+8÷（﹣4）

（2）解方程：+1＝

参考答案：见解析

解析：

【分析】（1）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值；

（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．

【解答】解：（1）原式＝×××（﹣8）+（﹣2）

＝﹣18﹣2

＝﹣20；

（2）去分母得：2（5x﹣7）+12＝3（3x﹣1）

去括号得：10x﹣14+12＝9x﹣3，

移项合并得：x＝﹣1．

第113题

规定“△”是一种新的运算法则，满足：a△b＝ab﹣3b．例如：2△（﹣3）＝2×（﹣3）﹣3×（﹣3）＝﹣6+9＝3．

（1）求﹣5△2的值；

参考答案：见解析

解析：

【分析】（1）原式利用题中的新定义计算即可求出值；

（2）已知等式利用题中的新定义化简，计算即可求出x的值．

【解答】解：（1）﹣5△2＝﹣5×2﹣3×2

＝﹣10﹣6

＝﹣16；

（2）﹣3△（x+1）＝x△（﹣2），

可得：﹣3（x+1）﹣3（x+1）＝﹣2x﹣3×（﹣2），

﹣3x﹣3﹣3x﹣3＝﹣2x+6，

﹣3x﹣3x+2x＝6+3+3，

﹣4x＝12，

x＝﹣3．

第114题

已知8x^2ay与﹣3x⁴y^2+b是同类项，且A＝a²+ab﹣2b²，B＝3a²﹣ab﹣6b²，求2B﹣3（B﹣A）的值．

参考答案：见解析

解析：

【分析】直接同类项的定义得出a，b的值，进而去括号合并同类项，再把a，b的值代入求出答案．

【解答】解：∵8x^2ay与﹣3x⁴y^2+b是同类项，

∴，

解得：，

∵A＝a²+ab﹣2b²，B＝3a²﹣ab﹣6b²，

∴2B﹣3（B﹣A）

＝3A﹣B

＝3（a²+ab﹣2b²）﹣（3a²﹣ab﹣6b²）

＝4ab，

当a＝2，b＝﹣1时，

原式＝4×2×（﹣1）＝﹣8．

第115题

如图，∠AOC＝80°，OB是∠AOC的平分线，OD是∠COE的平分线．

（1）求∠BOC的度数；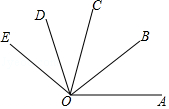

参考答案：见解析

解析：

【分析】（1）根据角平分线定义得出∠BOC＝∠AOC，代入求出即可；

（2）根据角平分线定义求出∠BOC和∠COE，再代入∠BOE＝∠BOC+∠COE求出即可．

【解答】解：（1）∵∠AOC＝80°，OB是∠AOC的平分线，

∴∠BOC＝∠AOC＝×80°＝40°；

（2）∵OB是∠AOC的平分线，OD是∠COE的平分线，∠AOC＝80°，∠DOE＝30°，

∴∠BOC＝∠AOC＝40°，∠COE＝2∠DOE＝60°，

∴∠BOE＝∠BOC+∠COE＝40°+60°＝100°．

第116题

列一元一次方程解应用题（两问均需用方程求解）

10月14日iPhone12在各大电商平台预约销售，预售不到24小时，天猫、京东等平台的iPhone12就被抢完，显示无货．为了加快生产进度，郑州一富士康工厂连夜帮苹果手机生产iPhone12中的某种AB型电子配件，这种配件由A型装置和B型装置组成．已知该工厂共有1200名工人．

参考答案：见解析

解析：

【分析】（1）设工厂里有x名工人生产B型装置，则有（3x﹣400）名工人生产A型装置，根据该工厂共有1200名工人列出方程即可求解；

（2）设工厂里有y名工人生产A型装置，则有（1200﹣y）名工人生产B型装置，根据AB型电子配件每套由2个A型装置和1个B型装置配套组成列出方程即可求解．

【解答】解：（1）设工厂里有x名工人生产B型装置，则有（3x﹣400）名工人生产A型装置，依题意有

x+3x﹣400＝1200，

解得x＝400．

故工厂里有400名工人生产B型装置；

（2）设工厂里有y名工人生产A型装置，则有（1200﹣y）名工人生产B型装置，依题意有

40y：30（1200﹣y）＝2：1，

解得y＝720，

则1200﹣y＝1200﹣720＝480．

故工厂里有y名工人生产720型装置，有480名工人生产B型装置．

第117题

2020年2月，湖北武汉笼罩在寒冬里，随着新冠肺炎疫情的变化发展，武汉这座处于风暴中心的城市历经了一系列的变化．城区内外的公共交通、网约出租车都已经被叫停，街面上的巡游出租车实行单双号限行．当公共交通停摆之后，摆在广大医务人员面前的通勤问题，就显得日益严峻．从2月1日起，阿里旗下高德打车联合武汉当地出行合作伙伴风韵出行，组织了公益志愿者车队，紧急上线“医护专车”服务．即日起，武汉市内所有医护人员均可通过高德打车，24小时免费呼叫专属且全方位安全防护的“医护专车”．志愿者小李某天下午的营运全是在金银潭医院进行的，假定以医院为起点，向南为正，向北为负，他这天下午的行程如下（单位：km）：+15，﹣3，+14，﹣11，+10，+4，﹣26

（1）小李在送第几位医护人员时行车里程最远，最远多少米？

参考答案：见解析

解析：

【分析】（1）比较各数绝对值的大小即可求解；

（2）计算各数的绝对值的和，再乘以每km的耗油量可求解．

【解答】解：（1）|26|＞|15|＞|+14|＞|﹣11|＞|+10|＞|+4|＞|﹣3|，

∴小李在送最后一位医护人员时行车里程最远，最远为26km＝26000m；

（2）0.1×（15+|﹣3|+14+|﹣11|+10+4+|﹣26|）＝8.3（升），

答：若汽车耗油量为0.1L/km，这天下午汽车共耗油8.3升．

第118题

某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过40立方米时，按2元/立方米计费；月用水量超过40立方米时，其中的40立方米仍按2元/立方米收费，超过部分按3.5元/立方米计费．设每户家庭月用水量为x立方米．

（1）当x不超过40时，应收水费为　　（用x的代数式表示）；当x超过40时，应收水费为　　（用x的代数式表示化简后的结果）；

参考答案：见解析

解析：

【分析】（1）根据题意，可以写出当x不超过40和当x超过40时相应的水费；

（2）根据题意，可以分别计算出四月份和五月份的水费，然后相加，即可解答本题；

（3）根据小明家六月份交水费150元，可以列出相应的方程，然后即可求得小明家这个月用水量多少立方米．

【解答】解：（1）由题意可得，

当x不超过40时，应收水费为2x元，

当当x超过40时，应收水费为：40×2+3.5（x﹣40）＝（3.5x﹣60）（元），

故答案为：2x元，（3.5x﹣60）元；

（2）由题意可得，

小明家四月份的水费为：26×2＝52（元），五月份的水费为3.5×52﹣60＝122（元），

∵52+122＝174（元），

∴小明家这两个月一共应交174元水费；

（3）设小明家这个月用水量x立方米，

∵40×2＝80＜150，

∴3.5x﹣60＝150，

解得x＝60，

答：小明家这个月用水量60立方米．

第119题

已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC．

参考答案：见解析

解析：

【分析】（1）由已知可求出∠BOC＝180°﹣∠AOC＝150°，再由∠COD是直角，OE平分∠BOC，即可求出∠DOE的度数；

（2）由（1）中的方法可得出结论∠DOE＝∠AOC，从而用含α的代数式表示出∠DOE的度数；

（3）设∠AOC＝α，则∠BOC＝180°﹣α，依据OE平分∠BOC，可得∠COE＝×（180°﹣α）＝90°﹣α，再依据∠COE＝2∠DOB，即可得到∠AOC的度数．

【解答】解：（1）由已知得∠BOC＝180°﹣∠AOC＝150°，

又∵∠COD是直角，OE平分∠BOC，

∴∠DOE＝∠COD﹣∠BOC＝90°﹣×150°＝15°；

（2）由（1）知∠DOE＝∠COD﹣∠BOC，

∴∠DOE＝90°﹣（180°﹣∠AOC）＝∠AOC＝α；

（3）设∠AOC＝α，则∠BOC＝180°﹣α，

∵OE平分∠BOC，

∴∠COE＝×（180°﹣α）＝90°﹣α，

如图②﹣1，∠BOD＝180°﹣90°﹣α＝90°﹣α，

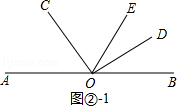
∵∠COE＝2∠DOB，

∴90°﹣α＝2（90°﹣α），

解得α＝60°．

如图②﹣2，∠BOD＝90°﹣（180°﹣α）＝α﹣90°，

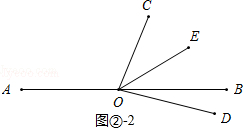
∵∠COE＝2∠DOB，

∴90°﹣α＝2（α﹣90°），

解得α＝108°．

综上所述，当∠AOC的度数是60°或108°时，∠COE＝2∠DOB

第120题

如图，由两块长方体叠成的几何体，从正面看它所得到的平面图形是(     )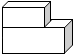

A.

B.

C.

D.

参考答案：A

解析：

【考点】简单组合体的三视图． 

【分析】细心观察图中几何体摆放的位置，根据主视图是从正面看到的图形判定即可．

【解答】解：长方体的主视图是：长方形，

此图有两个长方体组成，因此主视图是两个长方形，

再根据长方体的摆放可得：A正确，

故选；A．

【点评】此题主要考查了几何体的三视图，从正面看到的图叫做主视图，再注意长方体的摆放位置即可．