第261题

某市出租车的收费标准是：行程不超过3千米起步价为10元，超过3千米后每千米增收1.8元．某乘客出租车x千米．

（1）试用关于x的代数式分情况表示该乘客的付费．

参考答案：见解析

解析：

【考点】一元一次方程的应用；列代数式；代数式求值．

【分析】（1）需要分类讨论：行程不超过3千米和行程超过3千米，根据两种收费标准进行计算；

（2）把x=8代入（1）中相应的代数式进行求值即可；

（3）设他坐了x千米，根据该乘客付费26.2元列出方程求解即可．

【解答】解：（1）当行程不超过3千米即x≤3时时，收费10元；

当行程超过3千米即x＞3时，收费为：10+（x﹣3）×1.8=1.8x+4.6（元）．

（2）当x=8时，1.8x+4.6=1.8×8+4.6=19（元）．

答：乘客坐了8千米，应付费19元；

（3）设他坐了x千米，

由题意得：10+（x﹣3）×1.8=26.2，

解得x=12．

答：他乘坐了12千米．

【点评】该题考查了一元一次方程的应用，列代数式及求代数式的值等问题；解决问题的关键是读懂题意，找到所求的量的等量关系，进而列出式子．

第262题

如图，OM是∠AOC的平分线，ON是∠BOC的平分线．

参考答案：见解析

解析：

【考点】角的计算；角平分线的定义．

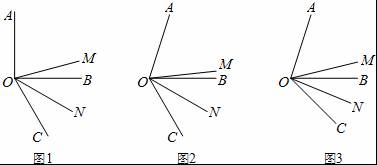
【分析】（1）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可；

（2）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可；

（3）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可．

【解答】解：（1）如图1，∵∠AOB=90°，∠BOC=60°，

∴∠AOC=90°+60°=150°，

∵OM平分∠AOC，ON平分∠BOC，

∴∠MOC=∠AOC=75°，∠NOC=∠BOC=30°

∴∠MON=∠MOC﹣∠NOC=45°．   

（2）如图2，

∵∠AOB=70°，∠BOC=60°，

∴∠AOC=70°+60°=130°，

∵OM平分∠AOC，ON平分∠BOC，

∴∠MOC=∠AOC=65°，∠NOC=∠BOC=30°

∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°．   

故答案为：35°．

（3）如图3，∠MON=α，与β的大小无关．    

理由：∵∠AOB=α，∠BOC=β，

∴∠AOC=α+β．         

∵OM是∠AOC的平分线，ON是∠BOC的平分线，

∴∠MOC=∠AOC=（α+β），

∠NOC=∠BOC=β，

∴∠AON=∠AOC﹣∠NOC=α+β﹣β=α+β．       

∴∠MON=∠MOC﹣∠NOC

=（α+β）﹣β=α           

即∠MON=α．

故答案为：α．

【点评】本题考查了角平分线定义和角的有关计算，关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC﹣∠NOC．

第263题

如图，已知数轴上点A，B是数轴上的一点，AB=12，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

（1）写出数轴上点B表示的数为　　，经t秒后点P走过的路程为　　（用含t的代数式表示）；

参考答案：见解析

解析：

【考点】一元一次方程的应用；数轴．

【专题】几何动点问题．

【分析】（1）设出B点表示的数为x，由数轴上两点间的距离即可得到x的方程，解方程即可得出x，由路程=速度×时间可得出点P走过的路程；

（2）设经t秒后P点追上Q点，根据题意可得，关于t的一元一次方程，解方程即可得出时间t；

（3）由P点位置的不同分两种情况考虑，依据中点的定义，可以找到线段间的关系，从而能找出MN的长度．

【解答】解：（1）设B点表示x，则有

AB=8﹣x=12，解得x=﹣4．

∵动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，

∴经t秒后点P走过的路程为6t．

故答案为：﹣4；6t．

（2）设经t秒后P点追上Q点，根据题意得：

6t﹣4t=12，

解得t=6．

答：经过6秒时间点P就能追上点Q．

（3）不论P点运动到哪里，线段MN都等于6．

分两种情况分析：

①点P在线段AB上时，如图1，

MN=PM+PN=PA+PB=（PA+PB）=AB=×12=6；

②点P在线段AB的延长线上时，如图2，

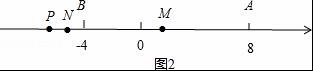
MN=PM﹣PN=PA﹣PB=（PA﹣PB）=AB=×12=6．

综上可知，不论P运动到哪里，线段MN的长度都不变，都等于6．

【点评】本题考查了数轴、中点依据解一元一次方程，解题的关键是：（1）找出关于x的一元一次方程；（2）找出关于时间t的一元一次方程；（3）由中点定义找到线段间的关系．