第141题

先化简再求值：3a+（﹣8a+2）﹣（3﹣4a），其中a=．

参考答案：见解析

解析：

【考点】整式的加减—化简求值． 

【专题】计算题；整式．

【分析】原式去括号合并得到最简结果，把a的值代入计算即可求出值．

【解答】解：原式=3a﹣8a+2﹣3+4a=﹣a﹣1，

当a=时，原式=﹣．

【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．

第142题

连州某旅行社组织甲、乙两个旅游团分别到西安、北京旅游，已知这两个旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人，问：

（1）若设乙旅行社的人数为x，请用含x的代数式表示甲旅行社的人数；

参考答案：见解析

解析：

【考点】一元一次方程的应用． 

【分析】（1）设甲旅游团个有x人，乙旅游团有（2x﹣5）人．

（2）根据题意可得等量关系：甲团+乙团=55人；甲团人数=乙团人数×2﹣5，根据等量关系列出方程，再解即可．

【解答】解：（1）乙旅游团有（2x﹣5）人．

（2）由题意得：2x﹣5+x=55，

解得：x=20，

所以2x﹣5=35（人）

答：甲旅游团有35人，乙旅游团有20人．

【点评】本题考查了一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．

第143题

某公园元旦期间，前往参观的人非常多．这期间某一天某一时段，随机调查了部分入园游客，统计了他们进园前等候检票的时间，并绘制成如下图表．表中“10～20”表示等候检票的时间大于或等于10min而小于20min，其它类同．

（1）这里采用的调查方式是__________（填“普查”或“抽样调查”），样本容量是__________；

参考答案：见解析

解析：

【考点】频数（率）分布直方图；频数（率）分布表；扇形统计图． 

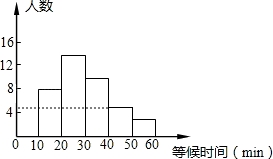
【分析】（1）由于前往参观的人非常多，5月中旬的一天某一时段，随机调查了部分入园游客，统计了他们进园前等候检票的时间，由此即可判断调查方式，根据已知的一组数据可以求出接受调查的总人数c；

（2）总人数乘以频率即可求出b，利用所有频率之和为1即可求出a，然后就可以补全频率分布直方图；

（3）用周角乘以其所在小组的频率即可求得其所在扇形的圆心角；

【解答】解：（1）填抽样调查或抽查；总人数为：8÷0.200=40；

（2）a=1﹣0.200﹣0.250﹣0.125﹣0.075=0.350；

b=8÷0.200×0.125=5；

频数分布直方图如图所示：

（3）“40～50”的圆心角的度数是0.125×360°=45°．

故答案为：抽样调查，40；a=0.350，b=5；45°．

【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．同时考查了中位数、频率和频数的定义．

第144题

观察下列关于自然数的等式：

3²﹣4×1²=5    ①

参考答案：见解析

解析：

【考点】规律型：数字的变化类；完全平方公式． 

【专题】规律型．

【分析】由①②③三个等式可得，被减数是从3开始连续奇数的平方，减数是从1开始连续自然数的平方的4倍，计算的结果是被减数的底数的2倍减1，由此规律得出答案即可．

【解答】解：（1）3²﹣4×1²=5    ①

5²﹣4×2²=9    ②

7²﹣4×3²=13   ③

…

所以第四个等式：9²﹣4×4²=17；

（2）第n个等式为：（2n+1）²﹣4n²=4n+1，

左边=（2n+1）²﹣4n²=4n²+4n+1﹣4n²=4n+1，

右边=4n+1．

左边=右边

∴（2n+1）²﹣4n²=4n+1．

【点评】此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．

第145题

6的相反数是（　　）

A.6

B.﹣6

C.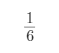 

D.﹣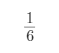

参考答案：B

解析：

【考点】相反数．

【分析】求一个数的相反数的方法就是在这个数的前边添加“﹣”，据此解答即可．

【解答】解：根据相反数的含义，可得

6的相反数是：﹣6．

故选：B．

【点评】此题主要考查了相反数的含义以及求法，要熟练掌握，解答此题的关键是要明确：相反数是成对出现的，不能单独存在；求一个数的相反数的方法就是在这个数的前边添加“﹣”．

第146题

如图所示的几何体是由一些小立方块搭成的，则这个几何体的左视图是（　　）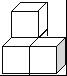

A.

B.

C.

D.

参考答案：A

解析：

【考点】简单组合体的三视图．

【专题】几何图形问题．

【分析】找到从左面看所得到的图形即可．

【解答】解：从左面可看到从左往右2列小正方形的个数依次为：2，1．

故选A．

【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．

第147题

在2015年深圳高交会上展出了现实版“钢铁侠”战衣﹣﹣马丁飞行喷射包，可连续飞行30分钟，载重120公斤，其网上预售价为160万元，数据160万元用科学记数法表示为（　　）

A.1.6×10⁴元

B.1.6×10⁵元

C.1.6×10⁶元

D.0.16×10⁷元

参考答案：C

解析：

【考点】科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【解答】解：160万=1600000=1.6×10⁶，

故选C．

【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

第148题

如图，现实生活中有部分行人选择横穿马路而不走天桥或斑马线，用数学知识解释这一现象的原因，可以为（　　）

A.过一点有无数条直线

B.两点之间线段的长度，叫做这两点之间的距离

C.两点确定一条直线

D.两点之间，线段最短

参考答案：D

解析：

【考点】线段的性质：两点之间线段最短．

【分析】根据线段的性质，直线的性质，可得答案．

【解答】解：现实生活中有部分行人选择横穿马路而不走天桥或斑马线，用数学知识解释这一现象的原因，两点之间线段最短．

故选：D．

【点评】本题考查了线段的性质，熟记性质并能灵活应用是解题关键．

第149题

小明每个月收集废电池a个，小亮比小明多收集20%，则小亮每个月收集的废电池数为（　　）

A.（a+20%）个

B.a（1+20%）个

C.个

D.个

参考答案：B

解析：

【考点】列代数式．

【分析】小亮比小明多收集20%，即每个月多20%a个，故小亮每个月收集的废电池数为a+20%a，提取a即使所得．

【解答】解：因为小亮比小明多收集20%，小明每个月手机废电池a个，

所以，多收集20%a个，

小亮每个月收集的废电池数为a+20%a=a（1+20%）．

故选B．

【点评】本题考查的列代数式，解题的关键是找对关系．

第150题

当前，“低头族”已成为热门话题之一，小颖为了解路边行人步行边低头看手机的情况，她应采用的收集数据的方式是（　　）

A.对学校的同学发放问卷进行调查

B.对在路边行走的学生随机发放问卷进行调查

C.对在路边行走的行人随机发放问卷进行调查

D.对在图书馆里看书的人发放问卷进行调查

参考答案：C

解析：

【考点】调查收集数据的过程与方法．

【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．

【解答】解：A、对学校的同学发放问卷进行调查不具代表性、广泛性，故A错误；

B、对在路边行走的学生随机发放问卷进行调查不具代表性、广泛性，故B错误；

C、对在路边行走的行人随机发放问卷进行调查具代表性、广泛性，故C正确；

D、对在图书馆里看书的人发放问卷进行调查不具代表性、广泛性，故D错误；

故选：C．

【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

第151题

如图，下列表示角的方法中，不正确的是（　　）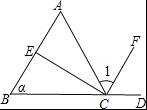

A.∠A

B.∠E

C.∠α

D.∠1

参考答案：B

解析：

【考点】角的概念．

【分析】先表示出各个角，再根据角的表示方法选出即可．

【解答】解：图中的角有∠A、∠1、∠α、∠AEC，

即表示方法不正确的有∠E，

故选B．

【点评】本题考查了对角的表示方法的应用，主要考查学生对角的表示方法的理解和掌握．

第152题

若x=3是方程ax+2x=14﹣a的解，则a的值为（　　）

A.10

B.5

C.4

D.2

参考答案：D

解析：

【考点】一元一次方程的解；解一元一次方程．

【专题】计算题；一次方程（组）及应用．

【分析】根据方程的解的概念，将x=3代入原方程，得到关于a的一元一次方程，解方程可得a的值．

【解答】解：根据题意，将x=3代入方程ax+2x=14﹣a，

得：3a+6=14﹣a，

移项，得：3a+a=14﹣6，

合并同类项，得：4a=8，

系数化为1，得：a=2．

故选：D．

【点评】本题主要考查方程的解的定义及解一元一次方程的能力，将方程的解代入原方程是关键．

第153题

小亮为表示出2015年他们家在“生活开支”项目的变化情况，他应该采用的统计图是（　　）

A.折线统计图

B.条形统计图

C.扇形统计图

D.以上均可以

参考答案：A

解析：

【考点】统计图的选择．

【分析】根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．

【解答】解：小亮为表示出2015年他们家在“生活开支”项目的变化情况，他应该采用的统计图是折线统计图，

故选：A．

【点评】本题考查了统计图的选择，此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断．

第154题

当x的值变大时，代数式﹣2x+3的值（　　）

A.变小

B.不变

C.变大

D.无法确定

参考答案：A

解析：

【考点】代数式求值．

【分析】令y=﹣2x+3，然后依据一次函数的性质求解即可．

【解答】解：令y=﹣2x+3．

∵﹣2＜0，

∴y随x的增大而减小．

∴代数式﹣2x+3的值随y的增大而减小．

故选：A．

【点评】本题主要考查的是代数式的值，将代数式问题转化为一次函数的增减性问题是解题的关键．

第155题

下列各式一定成立的是（　　）

A.﹣

B.|﹣a|=a

C.（﹣a）³=a³

D.（﹣a）²=a²

参考答案：D

解析：

【考点】有理数的乘方；绝对值．

【分析】根据乘方的定义判断ACD；根据绝对值的性质判B．

【解答】解：A、﹣=﹣，故选项错误；

B、a=﹣1时，|﹣a|=﹣a，故选项错误；

C、（﹣a）³=﹣a³，故选项错误；

D、（﹣a）²=a²，故选项正确．

故选：D．

【点评】考查了有理数的乘方，乘方的法则：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数；0的任何正整数次幂都是0．同时考查了绝对值的性质：如果用字母a表示有理数，则数a 绝对值要由字母a本身的取值来确定：①当a是正有理数时，a的绝对值是它本身a； ②当a是负有理数时，a的绝对值是它的相反数﹣a； ③当a是零时，a的绝对值是零．

第156题

把一副三角尺ABC与BDE按如图所示那样拼在一起，其中A、B、D三点在同一直线上，BM为∠CBE的平分线，BN为∠DBE的平分线，则∠MBN的度数是（　　）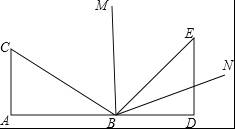

A.60°

B.67.5°

C.75°

D.85°

参考答案：C

解析：

【考点】角平分线的定义．

【分析】由角平分线的定义可知∠EBN===22.5°，由平角的定义可知∠CBE=180°﹣∠ABC﹣∠DBE=180°﹣30°﹣45°=105°，再利用角平分线的定义可得∠EBM，可得结果．

【解答】解：∵∠CBE=180°﹣∠ABC﹣∠DBE=180°﹣30°﹣45°=105°，BM为∠CBE的平分线，BN为∠DBE的平分线，

∴∠EBN===22.5°，=52.5°，

∴∠MBN=∠MBE+∠EBN=52.5°+22.5°=75°，

故选C．

【点评】本题主要考查了角平分线的定义，利用角平分线的定义计算角的度数是解答此题的关键．

第157题

如果节约20元记作+20元，那么浪费10元记作　　元．

参考答案：﹣10

解析：

【考点】正数和负数．

【分析】根据节约20元记作+20元，可以表示出浪费10元，本题得以解决．

【解答】解：∵节约20元记作+20元，

∴浪费10元记作﹣10元，

故答案为：﹣10．

【点评】本题考查正数和负数，解题的关键是明确正数和负数在题目中的实际含义．

第158题

若3a^m+3bⁿ⁺²与﹣2a⁵b是同类项，则mn=　　．

参考答案：﹣2

解析：

【考点】同类项．

【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程m+5=3，n=2，求出n，m的值，再代入代数式计算即可．

【解答】解：∵3a^m+3bⁿ⁺²与﹣2a⁵b是同类项，

∴m+3=5，n+2=1，

∴m=2，n=﹣1，

∴mn=2×（﹣1）=﹣2．

故答案为：﹣2．

【点评】本题考查同类项的定义、方程思想及负整数指数的意义，是一道基础题，比较容易解答．

第159题

一个正方体的每个面都有一个汉字，其平面展开图如图所示，那么在该正方体中与“价”字相对的字是　　．

参考答案：值

解析：

【考点】专题：正方体相对两个面上的文字．

【分析】正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，据此作答．

【解答】解：正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，

所以该正方体中与“价”字相对的字是值．

故答案为：值．

【点评】本题考查了正方体相对两个面上的文字．注意正方体的空间图形，从相对面入手，分析及解答问题．

第160题

如图是用小棒按一定规律摆成的一组图案，第1个图案中有5根小棒，第2个图案中有9个小棒，…，若第n个图案中有65根小棒，则n的值为　　．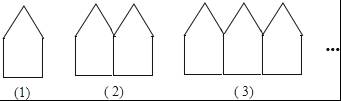

参考答案：16

解析：

【考点】规律型：图形的变化类．

【分析】依据数据5，9，13，再结合图形每次添加的部分为4根小棒，可得出每个图形所用小棒的根数与它当前是第几个图形之间的关系，代入数据，此题得解．

【解答】解：第一个图案5根小棒，第二个图象9根小棒，第三个图案13根小棒，结合图形发现每次添加的图形是第一个图形的一部分，

即每次添加4根小棒，且5=4+1，

故第n个图案的小棒数为4n+1，（n为正整数）

解4n+1=65，

得n=16．

故答案为16．

【点评】本题考查的图形的变换，解题的关键是找准每往后一幅图增加4个小棒，找准关系式套入数据即可．