第1题 （4分）规定一个物体向右移动1m，记作+1m，则这个物体向左移动了2m，可记作（　　）

A.﹣2m

B.2m

C.3m

D.﹣1m

参考答案：A

解析：

【分析】此题主要用正负数来表示具有意义相反的两种量：若向右移动正，则向左移动就记为负，直接得出结论即可．

【解答】解：规定一个物体向右移动1m，记作+1m，则这个物体向左移动了2m，可记作﹣2m．

故选：A．

第2题 （4分）下列说法正确的是（　　）

A.在所有连接两点的线中，直线最短

B.一个角的余角一定比这个角大

C.同角（或等角）的补角相等

D.经过两点有无数条直线

参考答案：C

解析：

【分析】根据“两点之间，线段最短“；互余的两个角的和为90°；补角的性质以及两点确定一条直线逐一判断即可．

【解答】解：A、在所有连接两点的线中，线段最短，故原说法错误，故本选项不合题意；

B、一个角的余角不一定比这个角大，如60°角的余角是30°，故原说法错误，故本选项不合题意；

C、同角（或等角）的补角相等，说法正确，故本选项符合题意；

D、经过两点有且只有一条直线，故原说法错误，故本选项不合题意；

故选：C．

第3题 （4分）新冠肺炎疫情爆发以来，口罩成为需求最为迫切的防护物资．在这个关键时刻，我国某企业3月份的口罩产能达到15500万只．“15500万只”用科学记数法表示为（　　）

A.1.55×10⁷只

B.1.55×10⁸只

C.0.155×10⁹只

D.1.55×10⁴只

参考答案：B

解析：

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．

【解答】解：15500万＝155000000＝1.55×10⁸，

故选：B．

第4题 （4分）下列各对数：+（﹣3）与﹣3；﹣（﹣3）与+（﹣3）；﹣（+3）与+（﹣3）；+3与+（﹣3）中，互为相反数的有（　　）

A.1对

B.2对

C.3对

D.4对

参考答案：B

解析：

【分析】根据相反数的定义判断即可．

【解答】解：+（﹣3）＝﹣3，﹣（﹣3）＝3，﹣（+3）＝﹣3，

故+（﹣3）与﹣3相等；﹣（﹣3）与+（﹣3）互为相反数；﹣（+3）与+（﹣3）相等；+3与+（﹣3）互为相反数，

所以互为相反数的有2对．

故选：B．

第5题

（4分）若关于x的方程（m﹣3）x^|m|﹣2﹣m+3＝0是一元一次方程，则m的值为（　　）

A.m＝3

B.m＝﹣3

C.m＝3或﹣3

D.m＝2或﹣2

参考答案：B

解析：

【分析】根据一元一次方程的定义得到m﹣3≠0且|m|﹣2＝1，由此求得m的值．

【解答】解：∵关于x的方程（m﹣3）x^|m|﹣2﹣m+3＝0是一元一次方程，

∴m﹣3≠0且|m|﹣2＝1，

解得m＝﹣3；

故选：B．

第6题

（4分）已知x＝3是关于x的方程ax+2x﹣3＝0的解，则a的值为（　　）

A.﹣1

B.﹣2

C.﹣3

D.1

参考答案：A

解析：

【分析】根据方程的解为x＝3，将x＝3代入方程即可求出a的值．

【解答】解：将x＝3代入方程得：3a+2×3﹣3＝0，

解得：a＝﹣1．

故选：A．

第7题

（4分）若多项式8x²﹣3x+5与多项式3x³+（m﹣4）x²﹣5x+7相加后，结果不含x²项，则常数m的值是（　　）

A.2

B.﹣4

C.﹣2

D.﹣8

参考答案：B

解析：

【分析】根据题意列出关系式，去括号合并后，根据结果不含x²项确定出m的值即可．

【解答】解：根据题意得：8x²﹣3x+5+3x³+（m﹣4）x²﹣5x+7

＝3x³+（m+4）x²﹣8x+12，

∵结果不含x²项，

∴m+4＝0，

解得：m＝﹣4．

故选：B．

第8题

（4分）若x＝|﹣2|，|y|＝3，则x﹣y的值为（　　）

A.﹣1

B.5

C.﹣1或5

D.±1或±5

参考答案：C

解析：

【分析】利用绝对值的意义得到x＝2，y＝±3，然后分别计算当x＝2，y＝3时和当x＝2，y＝﹣3时，x﹣y的值．

【解答】解：∵x＝|﹣2|，|y|＝3，

∴x＝2，y＝±3，

当x＝2，y＝3时，x﹣y＝2﹣3＝﹣1；

当x＝2，y＝﹣3时，x﹣y＝2﹣（﹣3）＝5，

综上所述，x﹣y的值为﹣1或5．

故选：C．

第9题

（4分）如图是由几个大小相同的小立方块搭成的几何体从上面看到的形状图，其中小正方形中的数字表示在该位置的小立方块的个数．则这个几何体从正面看到的形状图是（　　）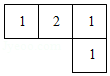

A.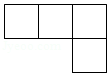

B.

C.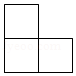

D.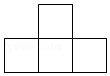

参考答案：D

解析：

【分析】根据提供的小立方块的个数从左到右确定主视图即可．

【解答】解：根据图形中小立方块的个数可知：这个几何体从正面看到的形状图共三列，从左到右依次是1、2、1个正方形，第2列上面1个正方形．

故选：D．

第10题

（4分）《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，可列方程为（　　）

A.8x﹣3＝7x+4

B.8x+3＝7x+4

C.8x﹣3＝7x﹣4

D.8x+3＝7x﹣4

参考答案：A

解析：

【分析】根据题意可以找出题目中的等量关系，列出相应的方程，就可以解答本题．

【解答】解：由题意可得，

设有x人，可列方程为：8x﹣3＝7x+4．

故选：A．

第11题

（4分）延长线段AB到C，使BC＝AB，若AC＝15，点D为线段AC的中点，则BD的长为（　　）

A.4.5

B.3.5

C.2.5

D.1.5

参考答案：A

解析：

【分析】设CB＝x，则AB＝4x，根据D是AC的中点求出AD的长，根据BD＝AD﹣AB即可得出结论．

【解答】解：设CB＝x，则AB＝4x，

∴AC＝AB+BC＝x+4x＝5x，

∵AC＝15，

∴x＝3，

∴AB＝12，

∵D是AC的中点，

∴AD＝AC＝×15＝7.5，

∴BD＝AB﹣AD＝12﹣7.5＝4.5．

故选：A．

第12题

（4分）规定图形表示运算a﹣b﹣c，图形表示运算x+z﹣y﹣w，则+的值是（　　）

A.﹣8

B.﹣6

C.0

D.2

参考答案：B

解析：

【分析】根据题目中的新运算，可以求得所求式子的值．

【解答】解：由题意可得，

+

＝（1﹣2﹣3）+（4+6﹣7﹣5）

＝（﹣4）+（﹣2）

＝﹣6，

故选：B．

第13题

（4分）A、B、C三点相对于海平面分别是﹣17米，+5米，﹣21米，那么最高的地方比最低的地方高　　米．

参考答案：26

解析：

【分析】用最高的地方高度减去最低的地方高度，列出算式，然后再依据有理数的减法法则计算即可．

【解答】解：最高的地方比最低的地方高：+5﹣（﹣21）＝5+21＝26（米）．

故答案为：26．

第14题

（4分）若单项式2x²y^m与﹣xⁿy³是同类项，则m+n＝　　．

参考答案：5

解析：

【分析】根据同类项的定义直接得到m＝3，n＝2，然后把它们代入m+n中进行计算即可．

【解答】解：由同类项的定义可知m＝3，n＝2，

则m+n＝3+2＝5．

故答案为：5．

第15题

（4分）如图，已知线段AB＝8cm，M是AB的中点，P是线段MB上一点，N为PB的中点，NB＝1.5cm，则线段MP＝　　cm．

参考答案：1

解析：

【分析】根据中点的定义可求解BM，及PB的长，进而可求解．

【解答】解：∵M是AB的中点，AB＝8cm，

∴AM＝BM＝4cm，

∵N为PB的中点，NB＝1.5cm，

∴PB＝2NB＝3cm，

∴MP＝BM﹣PB＝4﹣3＝1cm．

故答案为1．

第16题

（4分）定义一种对正整数n的“F”运算：①当n为奇数时，结果为n+1；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且运算重复进行，例如，取n＝40，则：

参考答案：1

解析：

【分析】根据题意，可以写出当n＝2020时的前几次结果，从而可以发现输出结果的变化特点，然后即可得到对n进行到第2021次“F”运算的结果．

【解答】解：由题意可得，

当n＝2020时，

第一次输出的结果为：505，

第二次输出的结果为：506，

第三次输出的结果为：253，

第四次输出的结果为：254，

第五次输出的结果为：127，

第六次输出的结果为：128，

第七次输出的结果为：1，

第八次输出的结果为：2，

第九次输出的结果为：1，

…，

∵（2021﹣6）÷2＝2015÷2＝1007…1，

∴对n进行到第2021次“F”运算的结果是1，

故答案为：1．

第17题

（8分）计算：

（1）23﹣17﹣（﹣7）+（﹣16）；

参考答案：见解析

解析：

【分析】（1）先同号相加，再异号相加；

（2）变形为（﹣26.54+18.54）+（6.4﹣6.4）进行计算即可求解；

（3）变形为（﹣0.5﹣7）+（3+2.75）进行计算即可求解；

（4）先算绝对值，再变形为+（﹣1﹣2+2.75）进行计算即可求解．

【解答】解：（1）23﹣17﹣（﹣7）+（﹣16）

＝23﹣17+7﹣16

＝（23+7）+（﹣17﹣16）

＝30﹣33

＝﹣3；

（2）（﹣26.54）﹣（﹣6.4）+18.54﹣6.4

＝（﹣26.54+18.54）+（6.4﹣6.4）

＝﹣8+0

＝﹣8；

（3）（﹣0.5）﹣（﹣3）+2.75﹣（+7）

＝（﹣0.5﹣7）+（3+2.75）

＝﹣8+6

＝﹣2；

（4）﹣|﹣1|﹣（+2）﹣（﹣2.75）

＝﹣1﹣2+2.75

＝+（﹣1﹣2+2.75）

＝﹣1

＝﹣．

第18题

（8分）解方程：

（1）3x+2＝7﹣2x；

参考答案：见解析

解析：

【分析】（1）方程移项，合并同类项，系数化1即可；

（2）方程去分母，去括号，移项，合并同类项，系数化1即可．

【解答】解：（1）3x+2＝7﹣2x，

移项，得3x+2x＝7﹣2，

合并同类项，得5x＝5，

系数化1，得x＝1；

（2），

去分母，得3（x+2）﹣2（2x﹣3）＝12，

去括号，得3x+6﹣4x+6＝12，

移项，得3x﹣4x＝12﹣6﹣6，

合并同类项，得﹣x＝0，

系数化1，得x＝0．

第19题

（10分）已知：A+B＝﹣3x²﹣5x﹣1，A﹣C＝﹣2x+3x²﹣5．

求：（1）B+C；

参考答案：见解析

解析：

【分析】（1）由A+B＝﹣3x²﹣5x﹣1，A﹣C＝﹣2x+3x²﹣5．可求出B+C的值；

（2）把x＝﹣1代入（1）中的代数式求值即可．

【解答】解：（1）∵A+B＝﹣3x²﹣5x﹣1，A﹣C＝﹣2x+3x²﹣5，

∴A+B﹣（A﹣C）＝﹣3x²﹣5x﹣1﹣（﹣2x+3x²﹣5），

∴B+C＝﹣3x²﹣5x﹣1+2x﹣3x²+5，

∴B+C＝﹣6x²﹣3x+4，

（2）把x＝﹣1代入﹣6x²﹣3x+4，得，

B+C＝﹣6×1﹣3×（﹣1）+4＝1．

第20题

（10分）已知：如图，∠AOB＝30°，∠COB＝20°，OC平分∠AOD，求∠BOD的度数．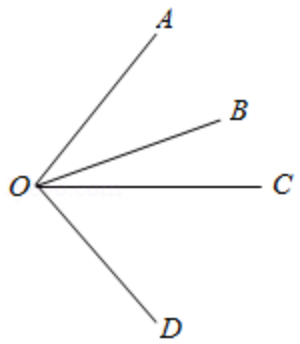

参考答案：见解析

解析：

【分析】根据角的和差、角平分线的定义，可得出答案．
【解答】解：∵∠AOB＝30°，∠COB＝20°，

∴∠AOC＝∠AOB+∠BOC＝30°+20°＝50°，

∵OC平分∠AOD，

∴∠AOC＝∠COD＝50°，

∴∠BOD＝∠BOC+∠COD＝20°+50°＝70°．