第81题

（4分）某车间有30名工人，生产某种由一个螺栓两个螺母组成的产品，每人每天生产螺母16个或螺栓22个，若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套，则下列所列方程正确的是（　　）

A.22x＝16（30﹣x）

B.16x＝22（30﹣x）

C.2×16x＝22（30﹣x）

D.2×22x＝16（30﹣x）

参考答案：D

解析：

【分析】设分配x名工人生产螺栓，则（30﹣x）人生产螺母，根据题意可得等量关系：螺母的数量＝螺栓的数量×2，然后再列出方程即可．

【解答】解：设分配x名工人生产螺栓，则（30﹣x）人生产螺母，由题意得：

2×22x＝16（30﹣x），

故选：D．

第82题

（4分）若|x﹣a|表示数轴上x与a两数对应的点之间的距离，当x取任意有理数时，代数式|x﹣6|+|x﹣2|的最小值为（　　）

A.5

B.4

C.3

D.2

参考答案：B

解析：

【分析】根据|x﹣a|表示数轴上x与a两数对应的点之间的距离，可知当x处于2和6中间时，|x﹣6|+|x﹣2|取得最小值，即为数轴上2和6之间的距离．

【解答】解：∵|x﹣a|表示数轴上x与a两数对应的点之间的距离，

∴|x﹣6|+|x﹣2|表示数轴上数x与6和数x与2对应的点之间的距离之和，

∴当2≤x≤6时，代数式|x﹣6|+|x﹣2|有最小值，最小值为|6﹣2|＝4，

故选：B．

第83题

（4分）如图所示，在这个数据运算程序中，若开始输入的x的值为2，结果输出的是1，返回进行第二次运算则输出的是﹣4，…，则第2021次输出的结果是（　　）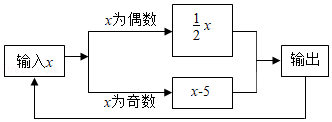

A.﹣6

B.﹣4

C.﹣1

D.﹣2

参考答案：A

解析：

【分析】根据题意和运算程序可以计算出前几次的输出结果，从而可以发现结果的变化特点，从而可以得到第2021次输出的结果，本题得以解决．

【解答】解：由题意可得，

第一次输出的结果为1，

第二次输出的结果为﹣4，

第三次输出的结果为﹣2，

第四次输出的结果为﹣1，

第五次输出的结果为﹣6，

第六次输出的结果为﹣3，

第七次输出的结果为﹣8，

第八次输出的结果为﹣4，

第九次输出的结果为﹣2，

…，

由上可得，从第二次输出结果开始，以﹣4，﹣2，﹣1，﹣6，﹣3，8依次循环出现，

∵（2021﹣1）÷6＝336…4，

∴第2021次输出的结果是﹣6，

故选：A．

第84题

（4分）若a、b互为相反数，c、d互为倒数，那么（a+b）²+|﹣cd|＝　　．

参考答案：1

解析：

【分析】由相反数和倒数的定义可知a+b＝0，cd＝1，然后代入计算即可求解．

【解答】解：∵a、b互为相反数，c、d互为倒数，

∴a+b＝0，cd＝1，

∴原式＝0²+1＝1．

故答案为：1．

第85题

（4分）若多项式x⁴﹣ax³+3x²+bx+x³﹣2x﹣5不含x³和x项，则a+b的值为　　．

参考答案：3

解析：

【分析】根据题意可得x³项和x项的系数等于0，进而可得a、b的值，然后可得a+b的值．

【解答】解：x⁴﹣ax³+3x²+bx+x³﹣2x﹣5

＝x⁴+（1﹣a）x³+3x²+（b﹣2）x+﹣5，

∵多项式x⁴﹣ax³+3x²+bx+x³﹣2x﹣5不含x³和x项，

∴1﹣a＝0，b﹣2＝0，

解得a＝1，b＝2，

∴a+b＝1+2＝3．

故答案为：3．

第86题

（4分）如图，已知线段AB＝8cm，M是AB的中点，P是线段MB上一点，N为PB的中点，NB＝1.5cm，则线段MP＝　　cm．

参考答案：1

解析：

【分析】根据中点的定义可求解BM，及PB的长，进而可求解．

【解答】解：∵M是AB的中点，AB＝8cm，

∴AM＝BM＝4cm，

∵N为PB的中点，NB＝1.5cm，

∴PB＝2NB＝3cm，

∴MP＝BM﹣PB＝4﹣3＝1cm．

故答案为1．

第87题

（4分）观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第10个图形共有　　个〇．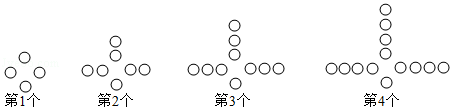

参考答案：31

解析：

【分析】观察图形的变化先得前几个图形中圆圈的个数，可以发现规律：第n个图形共有（3n+1）个〇，进而可得结果．

【解答】解：观察图形的变化可知：

第1个图形共有1×3+1＝4个〇；

第2个图形共有2×3+1＝7个〇；

第3个图形共有3×3+1＝10个〇；

…

所以第n个图形共有（3n+1）个〇；

所以第10个图形共有10×3+1＝31个〇；

故答案为：31．

第88题

（8分）计算

（1）6；

参考答案：见解析

解析：

【分析】（1）应用加法交换律、加法结合律，求出算式的值是多少即可．

（2）从左向右依次计算，求出算式的值是多少即可．

【解答】解：（1）6

＝[6﹣（﹣3）]+（3.3﹣3.3）+[﹣（﹣6）+4]

＝10+0+10

＝20．

（2）

＝36×÷（﹣16）

＝16÷（﹣16）

＝﹣1．

第89题

（8分）解方程：

（1）2x﹣（x+10）＝5x+2（x﹣1）；

参考答案：见解析

解析：

【分析】（1）方程去括号，移项，合并同类项，系数化1即可；

（2）方程去分母，去括号，移项，合并同类项，系数化1即可．

【解答】解：（1）2x﹣（x+10）＝5x+2（x﹣1），

去括号，得2x﹣x﹣10＝5x+2x﹣2，

移项，得2x﹣x﹣5x﹣2x＝10﹣2，

合并同类项，得﹣6x＝8，

系数化1，得x＝﹣；

（2），

去分母，得3（x+2）＝18﹣2（2x﹣1），

去括号，得3x+6＝18﹣4x+2，

移项，得3x+4x＝18+2﹣6，

合并同类项，7x＝14，

系数化1，得x＝2．

第90题

（10分）先化简，再求值：2（3x²﹣4xy）﹣4（2x²﹣3xy﹣1），其中|x﹣1|+（y+2）²＝0．

参考答案：见解析

解析：

【分析】首先去括号，然后再合并同类项，化简后，再代入x、y的值计算即可．

【解答】解：原式＝6x²﹣8xy﹣8x²+12xy+4

＝﹣2x²+4xy+4，

由|x﹣1|+（y+2）²＝0，

则x﹣1＝0，y+2＝0，

解得：x＝1，y＝﹣2，

当x＝1，y＝﹣2时，原式＝﹣2×1+4×1×（﹣2）+4＝﹣2﹣8+4＝﹣6．

第91题

（10分）如图所示，AB为一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE：∠BOD＝2：5，∠COE＝80°，求∠EOB的度数．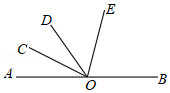

参考答案：见解析

解析：

【分析】设∠DOE＝2x，根据题意得到∠BOE＝3x，∠AOC＝∠COD＝80°﹣2x，再根据平角为180度，得到2×（80°﹣2x）+5x＝180°，解得x＝20°，即可得到∠BOE的度数．

【解答】解：如图，设∠DOE＝2x，

∵∠DOE：∠BOD＝2：5，

∴∠BOE＝3x，

又∵OC是∠AOD的平分线，∠COE＝80°，

∴∠AOC＝∠COD＝80°﹣2x

2×（80°﹣2x）+5x＝180°，

解得x＝20°

∴∠BOE＝3x＝3×20°＝60°．

故答案为：60°．

第92题

（12分）2018年9月7日，财政部和国税总局发布了《关于2018年第四季度个人所得税减除费用和税率适用问题的通知》，通知规定：我国自2018年10月1日起，个人所得税起征点从3500元提高到5000元．月收入不超过5000元的部分不收税；月收入超过5000元但不超过8000元的部分征收3%的个人所得……，例如：某人月收入6000元，他应缴纳个人所得税为（6000﹣5000）×3%＝30（元）．按此通知完成下面问题：

（1）某人月收入为5800元，他应缴纳个人所得税多少元？

参考答案：见解析

解析：

【分析】（1）根据题意，可以计算出某人月收入为5800元，他应缴纳个人所得税多少元；

（2）根据题意，可以用x的代数式表示出应缴纳个人所得税是多少元；

（3）根据题意和（2）中的结果，可以列出相应的方程，从而可以得到此人本月收入是多少元．

【解答】解：（1）由题意可得，

某人月收入为5800元，他应缴纳个人所得税为：（5800﹣5000）×3%＝800×3%＝24（元），

即某人月收入为5800元，他应缴纳个人所得税24元；

（2）由题意可得，

当月收入超过5000而又不超过8000元时，应缴纳个人所得税为（x﹣5000）×3%＝（3%x﹣150）（元），

即当月收入超过5000而又不超过8000元时，应缴纳个人所得税（3%x﹣150）元；

（3）设此人本月收入x元，

3%x﹣150＝78，

解得x＝7600，

答：此人本月收入7600元．

第93题

（12分）列方程解应用题：已知A，B两地相距60千米，甲骑自行车，乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地，乙每小时比甲多行30千米，甲比乙早出发3小时，乙出发1小时后刚好追上甲．

（1）求甲的速度；

参考答案：见解析

解析：

【分析】（1）设甲速度为x千米/小时，则乙速度为（x+30）千米/小时，根据题意可得等量关系：甲4小时的路程＝乙1小时的路程，根据等量关系列出方程，再解即可；

（2）设乙出发后t小时甲乙相距6千米，则甲出发（t+3）小时，本题有两种情况需要进行分类讨论，一种是甲乙相遇前，一种是甲乙相遇后分别列出方程，再解即可；

（3）设丙的速度为a千米/小时，丙与甲同时出发，所以丙行驶小时，乙行驶了﹣3＝小时，根据题意可得两人相遇则行驶路程和为AB两地之间的距离60千米．然后列出方程可得丙的速度，再求甲、丙两人之间距离．

【解答】解：（1）设甲速度为x千米/小时，则乙速度为（x+30）千米/小时

由题意可列方程：4x＝x+30

解得：x＝10

所以，甲速度为10千米/时；

（2）由（1）可知，甲速度为10千米/小时，乙速度为10+30＝40千米/小时，

设乙出发后t小时甲乙相距6千米，则甲出发（t+3）小时，

相遇前：甲比乙多行驶6千米，可列方程10（t+3）﹣40t＝6，

解得：t＝0.8，

相遇后：乙比甲多行驶6千米，可列方程40t﹣10（t+3）＝6，

解得t＝1.2，

综上所述，乙出发0.8小时或1.2小时，甲乙相距6千米；

（3）设丙的速度为a千米/小时，丙与甲同时出发，所以丙行驶小时，乙行驶了﹣3＝（小时）．

根据题意可列方程a+×40＝60，

解得：a＝10，

所以丙的速度为10千米/小时，

经过小时，丙行驶×10＝36（千米），甲行驶×10＝36（千米），

所以两人相距36+36﹣60＝12（千米）．

第94题

（12分）随着“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂每名工人计划每天生产200个医用口罩，一周生产1400个口罩．由于种种原因，实际每天生产量与计划量相比有出入．如表是工人小王某周的生产情况（超产记为正，减产记为负）：

参考答案：见解析

解析：

【分析】（1）用200减9即可；

（2）根据有理数的加法运算法则进行计算，再加上计划生产量即可；

（3）小王这一周的工资＝1400×0.6+超过部分数量×（0.6+0.15）．

【解答】解：（1）200﹣9＝191（个），

小王星期五生产口罩数量为191个．

故答案为：191；

（2）+5﹣2﹣4+13﹣9+15﹣8＝10（个），

则本周实际生产的数量为：1400+10＝1410（个）

答：小王本周实际生产口罩数量为1410个；

（3）一周超额完成的数量为10个，

所以，1400×0.6+10×（0.6+0.15）

＝840+7.5

＝847.5（元），

答：小王这一周的工资总额是847.5元．

第95题

（14分）如图，数轴上原点为O，A，B是数轴上的两点，点A对应的数是2，点B对应的数是﹣4，动点M，N同时从A、B出发，分别以1个单位/秒和3个单位/秒的速度沿着数轴正方向运动，设运动时间为t（t＞0）．

（1）AB两点间的距离是　　，动点M对应的数是　　，（用含t的代数式表示），动点N对应的数是　　．（用含t的代数式表示）

参考答案：见解析

解析：

【分析】（1）根据数轴上两点间的距离等于两点所表示的数的差的绝对值求出AB，然后根据路程＝速度×时间计算即可得解；

（2）根据①点O恰好为线段MN中点；②M、N交于一点列方程求出t，再求解即可；

（3）分①M，N在原点的两边；②M，N在原点的一边两种情况讨论求解．

【解答】解：（1）AB两点间的距离是2﹣（﹣4）＝6；

动点M对应的数是2+t；（用含t的代数式表示）

动点Q对应的数是﹣4+3t；（用含t的代数式表示）

故答案为：6，2+t，﹣4+3t；

（2）设经过t秒钟，点M与点N到原点O的距离相等，

①点O恰好为线段MN中点，依题意有

2+t+（﹣4+3t）＝0，

解得t＝0.5；

②M、N交于一点，依题意有

2+t＝﹣4+3t，

解得t＝3．

故经过0.5秒或3秒钟，点M与点N到原点O的距离相等；

（3）①M，N在原点的两边，

（2+t）：[﹣（﹣4+3t）]＝2：3，

解得t＝；

②M，N在原点的一边，

（2+t）：（﹣4+3t）＝2：3，

解得t＝．

故经过秒或秒钟，点M到原点O的距离OM与点N到原点O的距离ON恰好有OM：ON＝2：3．

第96题

《九章算术》中注“今两算得失相反，要令正负以名之”，意思是：有两数若其意义相反，则分别叫做正数和负数．若气温为零上10℃记作+10℃，则﹣8℃表示气温为（　　）

A.零上8℃

B.零下8℃

C.零上2℃

D.零下2℃

参考答案：B

解析：

【分析】此题主要用正负数来表示具有意义相反的两种量：若零上记为正，则零下就记为负，直接得出结论即可．

【解答】解：若气温为零上10℃记作+10℃，则﹣8℃表示气温为零下8℃．

故选：B．

第97题

在6，π，，0，，﹣（﹣3），40%，﹣|﹣4|各数中，正数的个数有（　　）

A.3

B.4

C.5

D.6

参考答案：C

解析：

【分析】根据正数的定义选出即可．

【解答】解：﹣（﹣3）＝3，﹣|﹣4|＝﹣4，

在6，π，，0，，﹣（﹣3），40%，﹣|﹣4|各数中，正数有6，π，，﹣（﹣3），40%共5个．

故选：C．

第98题

下列叙述正确的是（　　）

A.一个钝角和一个锐角一定互为补角

B.每一个锐角都有余角

C.两个锐角一定互为余角

D.一个钝角的余角是锐角

参考答案：B

解析：

【分析】根据余角和补角的概念判断即可．

【解答】解：A．一个锐角与一个钝角不一定互为补角，故本选项错误；

B．每一个锐角都有余角，故本选项正确；

C．只有两个锐角的和为90°时，这两个角才互余，故原说法错误；

D．钝角没有余角，故此选项错误；

故选：B．

第99题

2020年2月11日，联合国及农业组织向全球发出沙漠蝗虫灾害预警，30多个国家遭蝗虫灾难，巴基斯坦当前蝗虫数目约为4000亿只，4000亿用科学记数法表示为（　　）

A.4×10³亿

B.4×10⁷亿

C.4×10¹⁰亿

D.4×10¹¹亿

参考答案：A

解析：

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．

【解答】解：4000亿＝4×10³亿，

故选：A．

第100题

若关于x的方程（m﹣2）x^|m|﹣1＝6是一元一次方程，则m的值为（　　）

A.±2

B.﹣2

C.2

D.4

参考答案：B

解析：

【分析】只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程．它的一般形式是ax+b＝0（a，b是常数且a≠0）．则x的次数是1且系数不为0，即可得到关于m的方程，即可求解．

【解答】解：∵关于x的方程（m﹣2）x^|m|﹣1＝6是一元一次方程，

∴m﹣2≠0且|m|﹣1＝1，

解得：m＝﹣2，

故选：B．