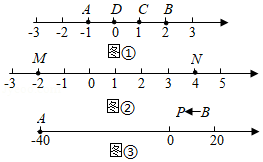第21题

（12分）一艘船从甲码头到乙码头顺流而行，用了2h；从乙码头返回甲码头逆流而行，用了2.5h．已知水流的速度是3km/h．

（1）求船在静水中的平均速度；

参考答案：见解析

解析：

【分析】（1）等量关系为：顺水速度×顺水时间＝逆水速度×逆水时间．即2×（静水速度+水流速度）＝2.5×（静水速度﹣水流速度）；

（2）由等量关系为：顺水速度×顺水时间＝逆水速度×逆水时间，列出方程，可求小艇在静水中速度，即可求解．

【解答】解：设船在静水中的平均速度为xkm/h，

根据往返路程相等，列得2（x+3）＝2.5（x﹣3），

解得x＝27．

答：在静水中的速度为27km/h．

（2）设小艇在静水中速度为ykm/h，从甲码头到乙码头所用时间为th，

由题意可得：t（y+3）＝2t（y﹣3），

∵t≠0，

∴y+3＝2（y﹣3），

解得 y＝9，

甲乙码头距离＝（27+3）×2＝60（km），

小艇从甲码头到乙码头所用时间：，

答：小艇从甲码头到乙码头所用时间为5小时．

第22题

（12分）“十•一”黄金周期间，大连圣亚海洋世界在8天假期中每天游客人数变化如下表（正号表示人数比前一天多，负号表示比前一天少），9月30日的游客人数为4.2万人．

参考答案：见解析

解析：

【分析】（1）根据题意列得算式，计算即可得到结果；

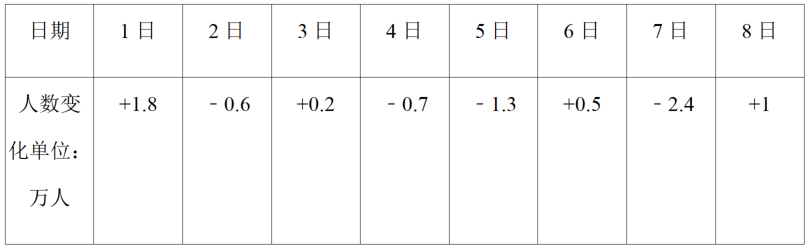
（2）根据表格找出旅客人数最多的与最少的，相减计算即可得到结果；

（3）根据表格得出1日到7日每天的人数，相加后再乘以100即可得到结果．

【解答】解：（1）根据题意列得：4.2+（1.8﹣0.6+0.2﹣0.7）＝4.9（万人）；故答案为：4.9；

（2）根据表格得：1日：4.2+1.8＝6（万人），

2日：6﹣0.6＝5.4（万人），

3日：5.4+0.2＝5.6（万人），

4日：5.6﹣0.7＝4.9（万人），

5日：4.9﹣1.3＝3.6（万人），

6日：3.6+0.5＝4.1（万人），

7日：4.1﹣2.4＝1.7（万人），

8日：1.7+1＝2.7（万人），

∴8天中旅客最多的是1日为6万人，最少的是7日为2.7万人，

则八天中旅客人数最多的一天比最少的一天多6﹣1.7＝4.3（万人）；

故答案为：4.3；

（3）根据表格得：每天旅客人数分别为6万人、5.4万人、5.6万人、4.9万人、3.6万人、4.1万人、1.7万人、2.7万人，则黄金周8天的旅游总收入约为（6+5.4+5.6+4.9+3.6+4.1+1.7+2.7）×80＝34×80＝2720（万元）．

答：圣亚海洋世界黄金周8天的旅游总收入约为2720万元．

第23题

（12分）某超市在春节期间对顾客实行优惠，规定如下：

参考答案：见解析

解析：

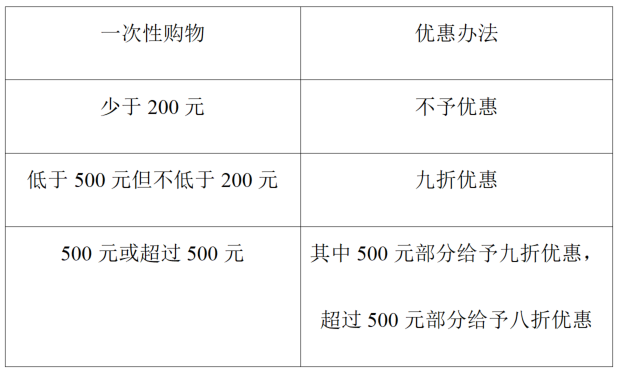
【分析】（1）让500元部分按9折付款，剩下的100按8折付款即可；可设王老师一次性购物x元，根据优惠条件结合实际付款270元，列出方程可求王老师一次性购物多少元；

（2）等量关系为：当x小于500元但不小于200时，实际付款＝购物款×9折；当x大于或等于500元时，实际付款＝500×9折+超过500的购物款×8折；

（3）两次购物王老师实际付款＝第一次购物款×9折+500×9折+（总购物款﹣第一次购物款﹣第二次购物款500）×8折，把相关数值代入即可求解．

【解答】解：（1）根据题意得：

500×0.9+（600﹣500）×0.8＝530（元）；

设王老师一次性购物x元，依题意有

0.9x＝270，

解得x＝300．

故他实际付款530元，王老师一次性购物300元；

故答案为：530，300；

（2）若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款0.9x元；

当x大于或等于500元时，他实际付款500×0.9+0.8（x﹣500）＝（0.8x+50）元，节省了x﹣（0.8x+50）＝（0.2x﹣50）元．

故答案为：0.9x；0.8x+50；（0.2x﹣50）；

（3）根据题意得：0.9a+0.8（850﹣a﹣500）+450＝（0.1a+730）元．

故两次购物王老师实际付款（0.1a+730）元；

当a＝250元时，0.1a+730＝25+730＝755，

850﹣755＝95（元）．

故王老师共节省了95元．

第24题

（14分）阅读理解：

点A、B、C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是有序点对[A，B]的好点．

参考答案：见解析

解析：

【分析】（1）根据定义计算BD、BC，验证是否具有BD＝2BC即可；

（2）根据定义计算2倍数量关系，MN＝6，6分成三份，一份为2，所以2表示的点符合题意；

（3）设点P表示的数为x，分情况讨论：

①计算出P运动的路程极为PB的长度，因为AB等于60，所以PA等于（60﹣2t）．

②分为5种情况：P为【A，B】的好点；A为【B，P】的好点；P为【B，A】的好点；A为【P，B】的好点；B为【A，P】的好点．

【解答】（1）因为BD＝2，BC＝1，BD＝2BC，所以B是[D，C]好点，但不是[C，D]好点．

（2）因为MN＝6，6÷3＝2，当为[M，N]好点是，左边距离是右边距离的2倍，所以左边为4个单位，右边为2个，所以这个数是2，或当N是中点时，这个数为10．

（3）①因为AB＝60，PB等于2t，所以AP等于60﹣2t．

②因为P、A和B中恰有一个点为其余两点的好点，所以分为5种情况讨论，分别如下：

第一种：P为【A，B】的好点，由题意 得，x﹣（﹣40）＝2（20﹣x），解得：x＝0，t＝20÷2＝10（秒）．

第二种：A为【B，P】的好点，由题意 得，20﹣（﹣40）＝2（x﹣（﹣40）），解得：x＝﹣10，t＝（20﹣（﹣10））÷2＝15（秒）．

第三种：P为【B，A】的好点，由题意 得，20﹣x＝2（x﹣（﹣40）），解得：x＝﹣20，t＝（20﹣（﹣20））÷2＝20（秒）．

第四种：A为【P，B】的好点，由题意 得，x﹣（﹣40）＝2（20﹣（﹣40）），解得：x＝80（舍）．

第五种：B为【A，P】的好点．由题意 得，20﹣（﹣40）＝2（20﹣x），解得：x＝﹣10，t＝（20﹣（﹣10））÷2＝15（秒）．

此种情况点 P 的位置与②中重合，即点 P 为 AB 中点．

综上可知，当 t 为 10 秒、15 秒或 20 秒，P、A 和 B 中恰有一个点为其余两点的好点．

第25题

（4分）在﹣（+2），﹣（﹣8），﹣5，﹣|﹣3|，+（﹣4）中，负数的个数有（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：D

解析：

【分析】负数就是小于0的数，依据定义即可求解．

【解答】解：在﹣（+2），﹣（﹣8），﹣5，﹣|﹣3|，+（﹣4）中，负数有在﹣（+2），﹣5，﹣|﹣3|，+（﹣4），一共4个．

故选：D．

第26题

（4分）下列说法中正确的是（　　）

A.直线有两个端点

B.互余的两个角不可能相等

C.相等的角是对顶角

D.两点之间，线段最短

参考答案：D

解析：

【分析】根据直线的性质，余角的定义，对顶角的性质，线段的性质对各选项分析判断后利用排除法求解．

【解答】解：A、直线有两个端点错误，故本选项错误；

B、45°的两个角互余也相等，故本选项错误；

C、相等的角不一定是对顶角，例如角平分线把角分成两个相等，故本选项错误；

D、两点之间，线段最短，故本选项正确．

故选：D．

第27题

（4分）某市今年累计向6500多名贫困学生发放资助资金约1179万元，此数据用科学记数法表示为（　　）

A.1.179×10⁶

B.1.179×10⁷

C.1.179×10⁸

D.1.179×10⁹

参考答案：B

解析：

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，10的指数n比原来的整数位数少1．

【解答】解：1179万＝1179 0000＝1.179×10⁷，

故选：B．

第28题

（4分）若a的倒数是﹣2，则a的相反数是（　　）

A.

B.2

C.﹣

D.﹣2

参考答案：A

解析：

【分析】根据倒数的定义得出a的值，再根据相反数的定义即可求解．

【解答】解：∵a的倒数是﹣2，

∴a＝﹣，

∴a的相反数是．

故选：A．

第29题

（4分）若方程2x－k x+1=5x－2的解为－1，则k的值为（　　）

A.10

B.－4

C.－6

D.－8

参考答案：C

解析：

【分析】把x=-1代入已知方程，列出关于k的新方程，通过解新方程来求k的值．

【解答】解：依题意，得

2×（-1）-（-1）k+1=5×（-1）-2，即-1+k=-7，

解得，k=-6．

故选：C．

第30题

（4分）把两张形状大小完全相同的小长方形卡片（如图1）不重复地放在一个底面为长方形（长为xcm，宽为ycm）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示．则图2中两块阴影部分周长的和是（　　）

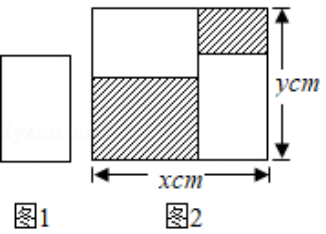
A.2（x+y） cm

B.4（x﹣y） cm

C.4xcm

D.4ycm

参考答案：D

解析：

【分析】设小长方形卡片的长为mcm，宽为ncm，由图形分别表示阴影部分两长方形的长与宽，进而表示出阴影部分的周长和，去括号合并后，即可得到结果．

【解答】解：设图1小长方形卡片的长为mcm，宽为ncm，

根据题意得：两块阴影部分的周长和为2[m+（y﹣n）]+2[n+（y﹣m）]

＝2（m+y﹣n+n﹣m+y）

＝2×2y

＝4y（cm）．

故选：D．

第31题

（4分）一个数的绝对值等于，那么这个数是（　　）

A.

B.

C.或

D.不能确定

参考答案：C

解析：

【分析】直接根据绝对值的意义求解．

【解答】解：绝对值等于的数为±．

故选：C．

第32题

（4分）由8个大小相同的正方体组成一个几何体，如图是分别从正面看和从上面看到的图形，则这个几何体从左面看到的图形是（　　）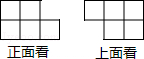

A.

B.

C.

D.

参考答案：B

解析：

【分析】根据主视图与俯视图可以估计出立方体的摆放，进而得出答案．

【解答】解：由从正面看和从上面看到的图形，可得，此几何体有两行，最左侧有2个正方体与第一行排齐，

下面一行中间部分至少有2个正方体摞列，则只有选项B符合题意．故选：B．

第33题

（4分）父亲今年32岁，儿子今年5岁，x年后父亲的年龄是儿子年龄的4倍，则x满足的方程是（　　）

A.32﹣x＝4（5﹣x）

B.32+x＝4（5+x）

C.32+x＝4×5

D.32﹣x＝4×5

参考答案：B

解析：

【分析】本题中存在的等量关系是：几年后，父亲的年龄＝儿子年龄的4倍．可以设x年后，这等量关系中的两个量：父亲的年龄和儿子年龄都可以表示出来，就可列方程求解．

【解答】解：设x年后，父亲的年龄是儿子年龄的4倍．

根据题意得到：32+x＝4（5+x）．

故选：B．

第34题

（4分）A，B，C三点在同一直线上，线段AB＝5cm，BC＝4cm，那么A，C两点的距离是（　　）

A.1cm

B.9cm

C.1cm或9cm

D.以上答案都不对

参考答案：C

解析：

【分析】由已知条件知A，B，C三点在同一直线上，做本题时应考虑到A、B、C三点之间的位置，分情况可以求出A，C两点的距离．

【解答】解：第一种情况：C点在AB之间上，故AC＝AB﹣BC＝1cm；

第二种情况：当C点在AB的延长线上时，AC＝AB+BC＝9cm．

故选：C．

第35题

（4分）如图所示的运算程序中，若开始输入的x值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，…第2019次输出的结果为（　　）

A.3

B.6

C.4

D.1

参考答案：B

解析：

【分析】根据题意可以写出前几次输出的结果，从而可以发现输出结果的变化规律，进而得到第2019次输出的结果．

【解答】解：由题意可得，

第1次输出的结果为24，

第2次输出的结果为12，

第3次输出的结果为6，

第4次输出的结果为3，

第5次输出的结果为6，

第6次输出的结果为3，

∵（2019﹣2）÷2＝1008…1，

∴第2019次输出的结果为6．

故选：B．

第36题

（4分）已知|a|＝1，|b|＝5，且a＞b，则a﹣b的值＝　　．

参考答案：6或4

解析：

【分析】根据绝对值的性质求出a、b的值，然后根据a＜b确定出a、b的对应情况，再相减即可得解．

【解答】解：∵|a|＝1，|b|＝5，

∴a＝±1，b＝±5，

∵a＞b，

∴a＝1时，b＝﹣5，a﹣b＝1﹣（﹣5）＝1+5＝6，

a＝﹣1时，b＝﹣5，a﹣b＝﹣1﹣（﹣5）＝﹣1+5＝4，

综上所述，a﹣b的值为6或4．

故答案为：6或4．

第37题

（4分）已知单项式﹣3a^m+5b³与是同类项，则mⁿ＝　　．

参考答案：81

解析：

【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程n﹣1＝2，m+2＝3，求出n，m的值，再代入代数式计算即可．

【解答】解：∵﹣3a^m+5b³与a²b^n﹣1是同类项，

∴m+5＝2，n﹣1＝3，

∴m＝﹣3，n＝4，

∴mⁿ＝（﹣3）⁴＝81．

故答案为：81．

第38题

（4分）如图，点C、D是线段AB的三等分点，如果点M、N分别是线段AC、BD的中点，那么MN：AB的值等于　　．

参考答案：2/3

解析：

【分析】由已知可求得MC+DN的长度，再根据MN＝MC+CD+DN不难求解．

【解答】解：∵点C、D是线段AB的三等分点，

∴AC＝CD＝BD＝AB，

M和N分别是AC和BD的中点，

∴MC＝AC＝AB，DN＝BD＝AB，

∴MN＝MC+DN+CD＝AB+AB+AB＝AB，

∴MN：AB＝，

故答案为：．

第39题

（4分）如果a，b是任意两个不等于零的数，定义运算⊕如下（其余符号意义如常）：a⊕b＝，那么[（1⊕2）⊕3]的值是　   　．

参考答案：1/12

解析：

【分析】按照定义运算⊕的计算法则代入求值即可．

【解答】解：根据题意，得[（1⊕2）⊕3]＝⊕3＝＝．

故答案是：．

第40题

（8分）（1）0﹣16+（﹣29）﹣（﹣7）﹣（+11）；

（2）（﹣1）+（﹣57）﹣（﹣1）+42；

参考答案：见解析

解析：

【分析】（1）从左向右依次计算即可．

（2）（3）（4）根据加法交换律、加法结合律计算即可．

【解答】解：（1）0﹣16+（﹣29）﹣（﹣7）﹣（+11）

＝﹣16﹣29+7﹣11

＝﹣49．

（2）（﹣1）+（﹣57）﹣（﹣1）+42

＝[（﹣1）﹣（﹣1）]+[（﹣57）+42]

＝0﹣15.3

＝﹣15.3．

（3）0.25+（﹣）﹣﹣|﹣|

＝（0.25﹣）+[（﹣）﹣|﹣|]

＝﹣0.5﹣1

＝﹣1.5．

（4）+（﹣2）﹣（﹣1）﹣（+0.5）

＝[﹣（﹣1）]+[（﹣2）﹣（+0.5）]

＝2﹣3

＝﹣1．