第61题

若﹣3x²y^b与x^ay是同类项，则（b﹣a）²⁰²⁰的值为　　．

参考答案：1

解析：

【分析】根据同类项是字母相同且相同字母的指数也相同，可得a、b的值，再代入所求式子计算即可．

【解答】解：∵﹣3x²y^b与x^ay是同类项，

∴a＝2，b＝1，

∴（b﹣a）²⁰²⁰＝（1﹣2）²⁰²⁰＝（﹣1）²⁰²⁰＝1．

故答案为：1．

第62题

如图，C、D两点是线段AB的三等分点，点M、N分别是线段AC、BD的中点，则MN＝　　AB．

参考答案：2/3

解析：

【分析】由已知可求得MC+DN的长度，再根据MN＝MC+CD+DN不难求解．

【解答】解：∵点C、D是线段AB的三等分点，

∴AC＝CD＝BD＝AB，

M和N分别是AC和BD的中点，

∴MC＝AC＝AB，DN＝BD＝AB，

∴MN＝MC+DN+CD＝AB+AB+AB＝AB，

故答案为：．

第63题

用棋子摆出下列一组“□”字，按照这种方法摆，则摆第7个“□”字需用棋子为　　枚．

参考答案：28

解析：

【分析】观察图形的变化写出前几个图形中棋子个数，进而可得第7个图形中棋子的个数．

【解答】解：观察图形的变化可知：

摆第1个“□”字需用棋子为4×1＝4枚，

摆第2个“□”字需用棋子为4×2＝8枚，

摆第3个“□”字需用棋子为4×3＝12枚，

…

所以摆第n个“□”字需用棋子为4n枚，

所以摆第7个“□”字需用棋子为4×7＝28枚．故答案为：28．

第64题

计算：

（1）（﹣36）×（+﹣）；

参考答案：见解析

解析：

【分析】（1）根据乘法分配律计算即可．

（2）首先计算乘方和括号里面的运算，然后计算括号外面的乘法和减法，求出算式的值是多少即可．

【解答】解：（1）（﹣36）×（+﹣）

＝（﹣36）×+（﹣36）×﹣（﹣36）×

＝﹣12﹣30+27

＝﹣15．

（2）﹣1⁴﹣（1﹣0.5）×（﹣1）×[2﹣（﹣3）²]

＝﹣1﹣×（﹣）×（﹣7）

＝﹣1﹣

＝﹣．

第65题

解方程：

（1）2x+3＝11﹣6x；

参考答案：见解析

解析：

【分析】（1）方程移项，合并同类项，系数化1即可；

（2）方程化简后，再移项，合并同类项，系数化1即可．

【解答】解：（1）2x+3＝11﹣6x，

移项，得2x+6x＝11﹣3，

合并同类项，得8x＝8，

系数化1，得x＝1；

（2）（3x﹣6）＝x﹣3，

去括号，得，

移项，得，

合并同类项，得，

系数化1，得x＝﹣20．

第66题

先化简，再求值：a²﹣（2a²﹣3b）+2（a²+b），其中，a＝﹣1，b＝1．

参考答案：见解析

解析：

【分析】先将a²﹣（2a²﹣3b）+2（a²+b）去括号，合并同类项，再将a＝﹣1，b＝1代入计算即可．

【解答】解：原式＝a²﹣2a²+3b+2a²+2b

＝（a²﹣2a²+2a²）+（3b+2b）

＝a²+5b，

当a＝﹣1，b＝1时，

原式＝（﹣1）²+5×1

＝6．

第67题

如图，∠AOB＝91°36'，∠AOC＝70°26'，且OM平分∠BOC，ON平分∠AOC，求∠MON的度数．

参考答案：见解析

解析：

【分析】由角的和差求出∠BOC＝162°2'，再根据角平分线的定义，角的和差，度分秒的换算求出∠MON的度数为45°48′．

【解答】解：如图所示：

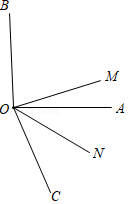
∵∠BOC＝∠AOB+∠AOC，

∠AOB＝91°36'，∠AOC＝70°26'，

∴∠BOC＝162°2'，

又∵OM平分∠BOC，

∴∠COM＝＝＝81°1'，

又∵ON平分∠AOC，

∴∠CON＝＝＝35°13′，

又∵∠COM＝∠CON+∠MON，

∴∠MON＝81°1'﹣35°13′＝45°48′．

第68题

机械厂加工车间有68名工人，平均每人每天加工大齿轮16个或小齿轮10个，已知2个大齿轮与3个小齿轮刚好配成1套，那么需要分别安排多少名工人加工大、小齿轮，才能使每天加工的大、小齿轮刚好配套？

参考答案：见解析

解析：

【分析】首先设需要安排x名工人加工大齿轮，则需要安排（68﹣x）名工人加工小齿轮，再利用2个大齿轮与3个小齿轮刚好配成1套得出方程求出答案．

【解答】解：设需要安排x名工人加工大齿轮，则需要安排（68﹣x）名工人加工小齿轮，依题意有

3×16x＝2×10（68﹣x），

解得x＝20，

68﹣x＝68﹣20＝48．

故需要安排20名工人加工大齿轮，需要安排48名工人加工小齿轮．

第69题

随着“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂每名工人计划每天生产200个医用口罩，一周生产1400个口罩．由于种种原因，实际每天生产量与计划量相比有出入．如表是工人小王某周的生产情况（超产记为正，减产记为负）：

参考答案：见解析

解析：

【分析】（1）用200减9即可；

（2）根据有理数的加法运算法则进行计算，再加上计划生产量即可；

（3）小王这一周的工资＝1400×0.6+超过部分数量×（0.6+0.15）．

【解答】解：（1）200﹣9＝191（个），

小王星期五生产口罩数量为191个．

故答案为：191；

（2）+5﹣2﹣4+13﹣9+15﹣8＝10（个），

则本周实际生产的数量为：1400+10＝1410（个）

答：小王本周实际生产口罩数量为1410个；

（3）一周超额完成的数量为10个，

所以，1400×0.6+10×（0.6+0.15）

＝840+7.5

＝847.5（元），

答：小王这一周的工资总额是847.5元．

第70题

某市从2019年1月1日开始实施阶梯电价制，居民生活用电价格方案如下：

参考答案：见解析

解析：

【分析】（1）根据400度在第3档列式计算即可得解；

（2）根据第3档的电费求法列方程计算即可得解．

【解答】解：（1）200×0.5+（350﹣200）×0.55+（400﹣350）×0.8＝222.5（元）．

故需交电费222.5元．

（2）月用电量为200度时，需交电费200×0.5＝100（元），

月用电量为350度时，需交电费200×0.5+（350﹣200）×0.55＝182.5（元），

月用电量为450度时，8月需交电费200×0.5+（450﹣200）×0.55＝237.5（元），9月需交电费200×0.5+（350﹣200）×0.55+（450﹣350）×0.8＝262.5（元），

所以小辰家2019年8月和9月用电量相同，共交电费660元的用电量在第3档．

设小辰家8月份用的用电量为x度，

则237.5+262.5+2（x﹣450）×0.8＝660，

解得x＝550．

答：小辰家8月份用550度电．

第71题

已知有理数a，b，c在数轴上对应的点分别为A，B，C，且满足（a﹣1）²+|ab+3|＝0，c＝﹣2a+b．

（1）分别求a，b，c的值；

参考答案：见解析

解析：

【分析】（1）绝对值和平方具有非负性，由非负数的和等于0，每个非负数都为零，求出a，b，c

（2）由数轴上两点间的距离公式表示出AD和BC，建立方程求解x．

（3）假设存在符合条件的k，表示3AC﹣kAB，再观察求解．

【解答】（1）∵（a﹣1）²≥0，|ab+3|≥0，（a﹣1）²+|ab+3|＝0，

∴a﹣1＝0，ab+3＝0，

∴a＝1，b＝﹣3，

又∵c＝﹣2a+b，

∴c＝﹣2×1+（﹣3）＝﹣5．

∴a＝1，b＝﹣3，c＝﹣5，

（2）由题意得：|x﹣1|＝4（﹣3+5），

∴x﹣1＝±8，

当x﹣1＝8时，x＝9，

当x﹣1＝﹣8时，x＝﹣7，

综上：x＝9或﹣7．

（3））假设存在符合条件的k，经过t秒，点A表示的数为1+2t，点B表示的数为﹣3+t，且A，B都在点C右侧，

∴AC＝1+2t﹣（﹣5）＝6+2t，

AB＝1+2t﹣（﹣3+t）＝4+t，

∴3AC﹣KAB＝3（6+2t）﹣K（4+t）＝18+6t﹣4k﹣kt＝18﹣4k+（6﹣k）t，

∵3AC﹣kAB的值在一定时间范围内不随运动时间t的改变而改变，

∴6﹣k＝0，

∴k＝6，

∴存在符合条件的k，

∴k＝6．

第72题

（4分）在﹣6，|﹣4|，﹣（+3），0，﹣（﹣2）中，负数共有（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：B

解析：

【分析】首先把|﹣4|，﹣（﹣3），﹣（﹣2）化简，然后再确定负数的个数．

【解答】解：|﹣4|＝4，﹣（﹣3）＝3，﹣|﹣2|＝﹣2，负数有﹣6，﹣2，共2个，

故选：B．

第73题

（4分）已知a与b互为相反数，则下列式子：①a+b＝0；②a＝﹣b；③a＝b；④＜0，其中一定成立的是（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：B

解析：

【分析】直接利用相反数的定义得出答案．

【解答】解：∵a与b互为相反数，

∴①a+b＝0，正确；②a＝﹣b，正确；③a＝b错误；④＜0（a≠0），原式错误，

故选：B．

第74题

（4分）一个角的余角是44°，这个角的补角是（　　）

A.134°

B.136°

C.156°

D.146°

参考答案：A

解析：

【分析】直接利用互为余角的定义得出这个角的度数，再利用互为补角的定义得出答案．

【解答】解：∵一个角的余角是44°，

∴这个角的度数是：90°﹣44°＝46°，

∴这个角的补角是：180°﹣46°＝134°．

故选：A．

第75题

（4分）2020年是“双11”的第12个年头，受前期疫情影响消费习惯发生大幅改变以及直播电商的快速发展，今年双11人们消费热情空前高涨．阿里巴巴数据显示，在11日0分26秒，天猫双11达到58.3万笔/秒的订单创建新峰值．把58.3万这个数据用科学记数法表示为（　　）

A.583×10³元

B.5.83×10⁶元

C.5.83×10⁵元

D.0.583×10⁶元

参考答案：C

解析：

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．

【解答】解：58.3万＝583000＝5.83×10⁵．

故选：C．

第76题

（4分）若关于x的方程（m﹣3）x^|m|﹣2﹣m+3＝0是一元一次方程，则m的值为（　　）

A.m＝3

B.m＝﹣3

C.m＝3或﹣3

D.m＝2或﹣2

参考答案：B

解析：

【分析】根据一元一次方程的定义得到m﹣3≠0且|m|﹣2＝1，由此求得m的值．

【解答】解：∵关于x的方程（m﹣3）x^|m|﹣2﹣m+3＝0是一元一次方程，

∴m﹣3≠0且|m|﹣2＝1，

解得m＝﹣3；

故选：B．

第77题

（4分）已知关于x的一元一次方程x﹣﹣1的解是偶数，则符合条件的所有整数a的和为（　　）

A.﹣12

B.﹣14

C.﹣20

D.﹣32

参考答案：A

解析：

【分析】先用含a的式子表示出原方程的解，再根据解为偶数，可求得a的值，则其和可求．

【解答】解：由x﹣﹣1得：6x﹣（3﹣ax）＝3（x+3）﹣6，

解得：x＝．

∵x的值是偶数，

∴3+a的值可能为1，3，﹣1、﹣3

∴a的值可能为﹣2，0，﹣4、﹣6，

∴符合条件的所有整数a的和是：﹣2+0﹣4﹣6＝﹣12．

故选：A．

第78题

（4分）下列说法正确的是（　　）

A.x²+x﹣1的常数项为1

B.单项式3²ab³的次数是6次

C.多项式是一次二项式

D.单项式﹣n的系数是﹣

参考答案：C

解析：

【分析】根据单项式次数、系数的定义，以及多项式的有关概念解答即可．

【解答】解：A、x²+x﹣1的常数项为﹣1，原说法错误，故此选项不符合题意；

B、单项式3²ab³的次数是4次，原说法错误，故此选项不符合题意；

C、多项式是一次二项式，原说法正确，故此选项符合题意；

D、单项式﹣的系数是﹣π，原说法错误，故此选项不符合题意．

故选：C．

第79题

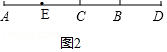
（4分）如图，C为线段AD上一点，点B为CD的中点，且AD＝9，BD＝2．若点E在直线AD上，且EA＝1，则BE的长为（　　）

A.4

B.6或8

C.6

D.8

参考答案：B

解析：

【分析】由于E在直线AD上位置不明定，可分E在线段DA的延长线和线段AD上两种情况求解．

【解答】解：若E在线段DA的延长线，如图1，

∵EA＝1，AD＝9，

∴ED＝EA+AD＝1+9＝10，

∵BD＝2，

∴BE＝ED﹣BD＝10﹣2＝8，

若E线段AD上，如图2，

EA＝1，AD＝9，

∴ED＝AD﹣EA＝9﹣1＝8，

∵BD＝2，

∴BE＝ED﹣BD＝8﹣2＝6，

综上所述，BE的长为8或6．

故选：B．

第80题

（4分）如图是正方体的展开图，则原正方体“4”与相对面上的数字之和是（　　）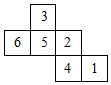

A.10

B.9

C.7

D.5

参考答案：C

解析：

【分析】根据正方体的展开图，原正方体“4”的相对面上的数字为3，再把两数相加即可得出答案．

【解答】解：∵正方体的展开图，原正方体“4”的相对面上的数字为3，

∴原正方体“4”与相对面上的数字之和是7．

故选：C．