第41题

（8分）我们可以用下面的方法把循环小数0.化成分数．

设x＝0.666…．则10x＝6.666…，可得方程10x﹣x＝6，解得x＝．即0.＝．用上面的方法解决下列问题：

参考答案：见解析

解析：

【分析】（1）设0.＝x，表示出10x，相减求出x的值即可；

（2）将0.＝y，表示出100y，相减即可求出y的值即可．

【解答】解：（1）设x＝0.，则10x＝5.，

可得10x﹣x＝5.﹣0.＝5，

解得：x＝；

（2）设y＝0.，则100y＝45.，

可得100y﹣y＝45，

解得：y＝，则原式＝+＝．

第42题

（10分）先化简，再求值：（5x²+4x﹣1）﹣4（x²+x），其中x＝﹣3．

参考答案：见解析

解析：

【分析】利用去括号、合并同类项进行化简后，再代入求值即可．

【解答】解：（5x²+4x﹣1）﹣4（x²+x）

＝5x²+4x﹣1﹣4x²﹣4x

＝x²﹣1，

当x＝﹣3时，原式＝9﹣1＝8．

第43题

（10分）如图，已知A，O，B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．

（1）若∠BOC＝62°，求∠DOE的度数；

参考答案：见解析

解析：

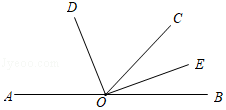
【分析】（1）根据角平分线的定义及角的和差计算即可；

（2）根据（1）用含α的式子计算即可；

（3）根据（1）、（2）所得结果即可得结论．

【解答】解：（1）∵OD平分∠AOC，OE平分∠BOC，

∴∠DOC＝∠AOC，∠COE＝∠BOC．

∴∠DOE＝∠DOC+∠COE

＝（∠BOC+∠COA）

＝×（62°+180°﹣62°）＝90°．

答：∠DOE的度数为90°

（2）∠DOE═（∠BOC+∠COA）

＝×（a+180°﹣a）＝90°．

答：∠DOE的度数为90°．

（3）∠DOE＝90°．理由如下：

设∠BOC＝x，

∠DOE═（∠BOC+∠COA）

＝×（x+180°﹣x）＝90°．

答：∠DOE的度数为90°．

第44题

（12分）如图，已知数轴上原点为O，点B表示的数为﹣2，A在B的右边，且A与B的距离是5，动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，设运动时间为t（t＞0）秒．

参考答案：见解析

解析：

【分析】（1）由点B表示的数、AB的长及点A在点B的右边，即可得出点A表示的数，再利用数轴上两点间的距离公式可求出与点A的距离为3的点表示的数；

（2）由点P，Q的出发点、运动速度及运动方向，可找出当运动时间为t秒时，点P，Q表示的数；

（3）由点P与点Q到点O距离相等，即可得出关于t的一元一次方程，解之即可得出结论．

【解答】解：（1）∵点B表示的数为﹣2，A在B的右边，且A与B的距离是5，

∴点A表示的数为﹣2+5＝3．

∵3﹣3＝0，3+3＝6，

∴与点A的距离为3的点表示的数是0或6．

故答案为：3；0或6．

（2）当运动时间为t秒时，点P表示的数为3t﹣2，点Q表示的数为﹣4t+3．

故答案为：（3t﹣2）；（﹣4t+3）．

（3）依题意，得：|3t﹣2|＝|﹣4t+3|，

即3t﹣2＝﹣4t+3或3t﹣2＝4t﹣3，

解得：t＝或t＝1．

答：当t＝或1时，点P与点Q到点O距离相等．

第45题

（12分）某人用400元购买了8套儿童服装，准备以一定的价格出售，如果以每套60元的价格为标准，超出的记为正数，不足的记为负数，记录如下：（单位：元）

+2，﹣3，+2，﹣1，﹣2，+1，﹣2，0．

参考答案：见解析

解析：

【分析】（1）以55元为标准记录的8个数字相加×8，即可求出结论；

（2）若盈利，就用卖衣服的总价钱﹣400就是盈利的钱，若亏损，就用400﹣买衣服的总价钱，就是亏损的钱．

【解答】解：（1）+2﹣3+2﹣1﹣2+1﹣2+0＝﹣3，

8×60﹣3＝477（元），

答：这8套服装后的总收入是477元；

（2）477+（﹣400）＝77（元），

答：盈利77元．

第46题

（12分）“湖田十月清霜堕，晚稻初香蟹如虎”，又到了食蟹的好季节啦！某经销商去水产批发市场采购太湖蟹，他看中了A、B两家的某种品质相近的太湖蟹．零售价都为60元/千克，批发价各不相同．

A家规定：批发数量不超过100千克，按零售价的92%优惠；批发数量超过100千克但不超过200千克，按零售价的90%优惠；超过200千克的按零售价的88%优惠．

参考答案：见解析

解析：

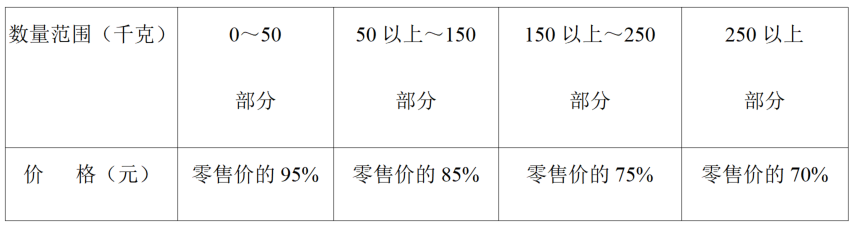
【分析】（1）根据A、B两家的优惠办法分别求出两家购买需要的费用就可以了．

（2）根据题意列出式子分别表示出购买x千克太湖蟹所相应的费用就可以了．

（3）当x＝195分别代入（2）的表示A、B两家费用的两个式子，然后再比较其大小就可以．

【解答】解：（1）由题意，得：

A：80×60×92%＝4416元，

B：50×60×95%+30×60×85%＝4380元．

（2）由题意，得

A：60×90%x＝54x，

B：50×60×95%+100×60×85%+（x﹣150）×60×75%＝45x+1200．

（3）当x＝195时，

A：54×195＝10530，

B：45×195+1200＝9975，

∴10530＞9975，

∴B家优惠．

第47题

（14分）如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”，图中点A表示﹣20，点B表示m，点C表示40，我们称点A和点C在数轴上相距60个长度单位，用式子表示为AC＝60，动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，运动到B点停止；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后立刻恢复原速，当P停止运动后，Q也随之停止运动，设运动的时间为t秒，问：

（1）BC＝　　（用含m的式子表示）；

参考答案：见解析

解析：

【分析】（1）根据两点间的距离公式即可求解；

（2）先求出动点P的运动时间，再根据时间的等量关系列出方程计算即可求解；

（3）分三种情况：当t≤10时；当10＜t＜25时；当t≥25时；进行讨论即可求解．

【解答】解：（1）BC＝40﹣m．

故答案为：40﹣m；

（2）（秒），

，

解得m＝30；

（3）当t≤10时，P：﹣20+2t，Q：40﹣t，

依题意有（40﹣t）﹣（﹣20+2t）＝40，

解得；

当10＜t＜25时，PQ≠40；

当t≥25时，P：t﹣10，Q：25﹣t，

依题意有（t﹣10）﹣（25﹣t）＝40．

解得．

综上：或．

第48题

下列四个数中，最小的数是（　　）

A.7

B.﹣1

C.0

D.﹣

参考答案：B

解析：

【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．

【解答】解：∵，

∴最小的数是﹣1．

故选：B．

第49题

已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（　　）

A.120°

B.60°

C.30°

D.150°

参考答案：D

解析：

【分析】根据∠1和∠2互为余角，∠1＝60°，求得∠2的度数，然后根据∠2与∠3互补，得出∠3＝180°﹣∠2．

【解答】解：∵∠1和∠2互为余角，∠1＝60°，

∴∠2＝90°﹣∠1＝90°﹣60°＝30°，

∵∠2与∠3互补，

∴∠3＝180°﹣∠2＝180°﹣30°＝150°．

故选：D．

第50题

在，125%，﹣25，0，﹣0.3，0.67，﹣4，中，非负数有（　　）

A.2 个

B.3 个

C.4 个

D.5 个

参考答案：C

解析：

【分析】根据非负数包括正数和0判断即可．

【解答】解：在，125%，﹣25，0，﹣0.3，0.67，﹣4，中，非负数有在，125%，0，0.67共4个．

故选：C．

第51题

新型冠状病毒肺炎是一种急性感染性肺炎，其病原体是一种先前未在人类中发现的新型冠状病毒，即2019新型冠状病毒．截止到2020年9月21日5时38分，全球新冠肺炎累计确诊病例突破3118万例．把3118万例用科学记数法表示为（　　）例．

A.31.18×10⁶

B.0.3118×10⁸

C.3.118×10⁸

D.3.118×10⁷

参考答案：D

解析：

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．

【解答】解：3118万＝31180000＝3.118×10⁷．

故选：D．

第52题

下列方程的变形正确的是（　　）

A.由3x﹣2＝2x+1移项，得3x﹣2x＝﹣1+2

B.由3﹣x＝2﹣5（x﹣1）去括号，得3﹣x＝2﹣5x﹣5

C.由系数化为1，得x＝1

D.由去分母，得3x﹣2（x﹣1）＝18

参考答案：D

解析：

【分析】各项中方程变形得到结果，即可做出判断．

【解答】解：A、由3x﹣2＝2x+1移项，得3x﹣2x＝1+2，故选项错误；

B、由3﹣x＝2﹣5（x﹣1）去括号，得3﹣x＝2﹣5x+5，故选项错误；

C、由系数化为1，得x＝﹣1，故选项错误；

D、由去分母，得3x﹣2（x﹣1）＝18，故选项正确．

故选：D．

第53题

已知关于x的方程a+x＝5﹣（2a+1）x的解是x＝﹣1，则a的值是（　　）

A.﹣5

B.﹣6

C.﹣7

D.8

参考答案：C

解析：

【分析】根据方程解的定义，将方程的解代入方程可得关于字母系数a的一元一次方程，从而可求出a的值．

【解答】解：把x＝﹣1代入原方程得a﹣1＝5﹣（2a+1）×（﹣1），解得a＝﹣7．

故选：C．

第54题

一多项式与2a²+3a﹣7的和为a²﹣4a+9，则这个多项式为（　　）

A.﹣a²﹣a+2

B.﹣a²﹣7a+16

C.﹣a²﹣a+16

D.3a²﹣a+2

参考答案：B

解析：

【分析】根据和减去一个加数等于另一个加数，计算即可．

【解答】解：根据题意得：（a²﹣4a+9）﹣（2a²+3a﹣7）

＝a²﹣4a+9﹣2a²﹣3a+7

＝﹣a²﹣7a+16．

故选：B．

第55题

在数轴上，表示数x的点的位置如图所示，则化简|x+1|﹣|x﹣2|结果为（　　）

A.3

B.﹣3

C.2x﹣1

D.1﹣2x

参考答案：C

解析：

【分析】直接利用数轴得出x的取值范围，再利用绝对值的性质化简得出答案．

【解答】解：由数轴可得：﹣1＜x＜0，

则x+1＞0，x﹣2＜0，

故|x+1|﹣|x﹣2|

＝x+1﹣[﹣（x﹣2）]

＝x+1+x﹣2

＝2x﹣1．

故选：C．

第56题

一个正方体的平面展开图如图所示，每一个面都写有一个整数，并且相对两个面上所写的两个整数之和都相等，则mn的值为（　　）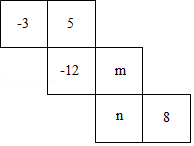

A.8

B.9

C.﹣7

D.﹣6

参考答案：B

解析：

【分析】利用正方体及其表面展开图的特点以及题意解题，把﹣12作为正方体的底面，然后把平面展开图折成正方体，然后根据两个相对面整数之和相等求出m、n．

【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“m”与面“﹣3”相对，面“n”与面“5”相对，“﹣12”与面“8”相对．

∵相对两个面上所写的两个整数之和都相等，且﹣12+8＝﹣4，

∴m﹣3＝﹣4，n+5＝﹣4，

解得m＝﹣1，n＝﹣9．

∴mn的值为9，

故选：B．

第57题

我国古代有很多经典的数学题，其中有一道题目是：良马日行二百里，驽马日行一百二十里，驽马先行十日，问良马几何追及之．意思是：跑得快的马每天走200里，跑得慢的马每天走120里，慢马先走10天，快马几天可追上慢马？若设快马x天可追上慢马，则由题意可列方程为（　　）

A.120+10x＝200x

B.120x+200x＝120×10

C.200x＝120x+200×10

D.200x＝120x+120×10

参考答案：D

解析：

【分析】设快马x天可以追上慢马，根据快马和慢马所走的路程相等建立方程即可．

【解答】解：设快马x天可以追上慢马，

依题意，得：200x＝120x+120×10．

故选：D．

第58题

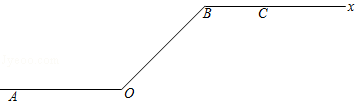
如图，C，D是线段AB上的两点，E是AC的中点，F是BD的中点，若AB＝10，CD＝4，则EF的长为（　　）

A.6

B.7

C.5

D.8

参考答案：B

解析：

【分析】根据线段的和差，可得（AC+DB）的长度，根据线段中点的性质，可得（AE+BF）的长度，再根据线段的和差，可得答案．

【解答】解：由线段的和差，得AC+DB＝AB﹣CD＝10﹣4＝6．

∵点E是AC的中点，

∴AE＝AC，

∵点F是BD的中点，

∴BF＝BD，

∴AE+BF＝（AC+DB）＝3．

由线段的和差，得

EF＝AB﹣（AE+BF）＝10﹣3＝7．

故选：B．

第59题

观察下列各等式：

﹣2+3＝1

A.﹣130

B.﹣131

C.﹣132

D.﹣133

参考答案：C

解析：

【分析】根据题目中的等式，可以发现每一行等号右边的数字都是这一行对应数字的平方，而等号左边的数字一半是负的，一半是正的，都跟等号右边的数字有关，从而可以写出第n个式子，进而得到第11行左起第11个数．

【解答】解：∵﹣2+3＝1，

﹣5﹣6+7+8＝4，

﹣10﹣11﹣12+13+14+15＝9，

﹣17﹣18﹣19﹣20+21+22+23+24＝16，

…，

∴第n个式子是﹣（n²+1）﹣（n²+2）﹣…﹣（n²+n）+（n²+n+1）+…+（n²+2n）＝n²，

∴第11行左起第11个数：﹣（11²+11）＝﹣132，

故选：C．

第60题

若有理数x、y互为倒数，则（xy﹣2）²⁰¹⁸＝　　．

参考答案：1

解析：

【分析】根据有理数x、y互为倒数，可以得到xy＝1，然后即可求得所求式子的值．

【解答】解：∵x、y互为倒数，

∴xy＝1，

∴（xy﹣2）²⁰¹⁸

＝（1﹣2）²⁰¹⁸

＝（﹣1）²⁰¹⁸

＝1，

故答案为：1．