七年级数学上学期期末测试卷集【人教版】（263题）

---

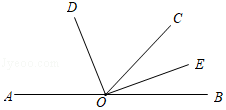
（10分）如图，已知A，O，B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．

（1）若∠BOC＝62°，求∠DOE的度数；

（2）若∠BOC＝α，求∠DOE的度数；

（3）通过（1）（2）的计算，你能总结出什么结论，直接简写出来，不用说明理由．

知识点：模拟卷02

参考答案：见解析

解析：

【分析】（1）根据角平分线的定义及角的和差计算即可；

（2）根据（1）用含α的式子计算即可；

（3）根据（1）、（2）所得结果即可得结论．

【解答】解：（1）∵OD平分∠AOC，OE平分∠BOC，

∴∠DOC＝∠AOC，∠COE＝∠BOC．

∴∠DOE＝∠DOC+∠COE

＝（∠BOC+∠COA）

＝×（62°+180°﹣62°）＝90°．

答：∠DOE的度数为90°

（2）∠DOE═（∠BOC+∠COA）

＝×（a+180°﹣a）＝90°．

答：∠DOE的度数为90°．

（3）∠DOE＝90°．理由如下：

设∠BOC＝x，

∠DOE═（∠BOC+∠COA）

＝×（x+180°﹣x）＝90°．

答：∠DOE的度数为90°．