七年级数学上学期期末测试卷集【人教版】（263题）

---

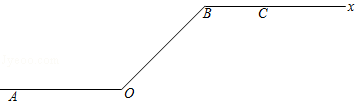
（14分）如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”，图中点A表示﹣20，点B表示m，点C表示40，我们称点A和点C在数轴上相距60个长度单位，用式子表示为AC＝60，动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，运动到B点停止；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后立刻恢复原速，当P停止运动后，Q也随之停止运动，设运动的时间为t秒，问：

（1）BC＝　　（用含m的式子表示）；

（2）若P、Q两点在数轴上点O至点B之间的D点相遇，D点表示10，求m；

（3）在（2）的条件下，当PQ＝40时，求t．

知识点：模拟卷02

参考答案：见解析

解析：

【分析】（1）根据两点间的距离公式即可求解；

（2）先求出动点P的运动时间，再根据时间的等量关系列出方程计算即可求解；

（3）分三种情况：当t≤10时；当10＜t＜25时；当t≥25时；进行讨论即可求解．

【解答】解：（1）BC＝40﹣m．

故答案为：40﹣m；

（2）（秒），

，

解得m＝30；

（3）当t≤10时，P：﹣20+2t，Q：40﹣t，

依题意有（40﹣t）﹣（﹣20+2t）＝40，

解得；

当10＜t＜25时，PQ≠40；

当t≥25时，P：t﹣10，Q：25﹣t，

依题意有（t﹣10）﹣（25﹣t）＝40．

解得．

综上：或．