第161题

计算：

（1）﹣14﹣（﹣22）+（﹣36）．

参考答案：见解析

解析：

【考点】有理数的混合运算．

【专题】计算题；实数．

【分析】（1）原式利用减法法则变形，计算即可得到结果；

（2）原式先计算乘方及绝对值运算，再计算乘法运算，最后算加减运算即可得到结果．

【解答】解：（1）原式=﹣14+22﹣36=﹣50+22=﹣28；

（2）原式=﹣4+36×（﹣）=﹣4+27﹣8=﹣12+27=15．

【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

第162题

（1）化简：﹣3（x²+2xy）+6（x²﹣xy）

（2）先化简，再求代数式的值：2（x²y+xy²）﹣2（x²y﹣2）﹣（xy²+2），其中x=2015，y=﹣1．

参考答案：见解析

解析：

【考点】整式的加减—化简求值；整式的加减．

【专题】计算题；整式．

【分析】（1）原式去括号合并即可得到结果；

（2）原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．

【解答】解：（1）原式=﹣3x²﹣6xy+6x²﹣6xy=3x²﹣12xy；

（2）原式=2x²y+2xy²﹣2x²y+4﹣xy²﹣2=xy²+2，

当x=2015，y=﹣1时，原式=2015×（﹣1）²+2=2017．

【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．

第163题

（1）解方程：5x+12=2x﹣9

（2）解方程：．

参考答案：见解析

解析：

【考点】解一元一次方程．

【专题】计算题；一次方程（组）及应用．

【分析】（1）按照解一元一次方程的步骤：移项、合并同类项、系数化为1，逐步进行即可；

（2）按照解一元一次方程的步骤：去分母、去括号、移项、合并同类项、系数化为1，逐步进行即可．

【解答】解：（1）移项，得：5x﹣2x=﹣9﹣12，

合并同类项，得：3x=﹣21，

系数化为1，得：x=﹣7

（2）去分母，得：5（ x﹣2 ）=20﹣2（ 2x﹣3 ），

去括号，得：5x﹣10=20﹣4x+6，

移项，得：5x+4x=20+6+10，

合并同类项，得：9x=36，

系数化为1，得：x=4．

【点评】本题主要考查学生解一元一次方程的基本技能，严格遵循解方程的一般步骤逐步进行是根本，属基础题．

第164题

2015年，深圳市人居环境委通报了2014年深圳市大气PM2.5来源研究成果．报告显示主要来源有，A：机动车尾气，B：工业VOC转化及其他工业过程，C：扬尘，D：远洋船，E：电厂，F：其它．某教学学习小组根据这些数据绘制出了如下两幅尚不完整的统计图（图1，图2）．

参考答案：见解析

解析：

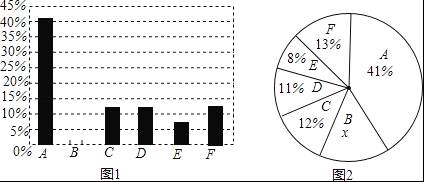
【考点】条形统计图；扇形统计图．

【专题】计算题；图表型；数据的收集与整理．

【分析】（1）B所占百分率等于1减去其他所有百分率之和；

（2）由（1）知B所占百分率为15%，可补全统计图；

（3）A所在扇形圆心角度数等于A的百分率乘以360度．

【解答】解：（1）根据扇形统计图可知，B所占百分率为：1﹣（41%+12%+11%+8%+13%）=15%；

（2）由（1）可知B所占百分率为15%，补全条形统计图如下：

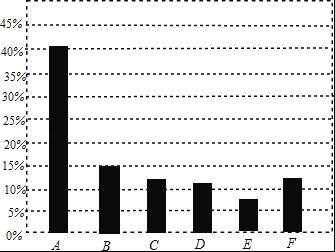
（3）“A：机动车尾气”所在扇形的圆心角度数为：41%×360°=147.6°．

故答案为：（1）15%，（2）147.6°．

【点评】本题主要考查从统计图表中获取有用信息的能力，理解各项百分率之和为1和圆心角与百分率间关系是此题关键．

第165题

如图，平面上有射线AP和点B、点C，按下列语句要求画图：

（1）连接AB；

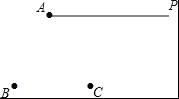
参考答案：见解析

解析：

【考点】直线、射线、线段．

【专题】作图题．

【分析】（1）根据要求画出射线及直线即可；

（2）射线AP上截取线段AD=AB即可；

（3）延长线部分画虚线；

（4）连接两点D、E．

【解答】解：如图所示：（1）连接AB；

（2）用尺规在射线AP上截取AD=AB；

（3）连接BC，并延长BC到E，使CE=BC；（4）连接DE．

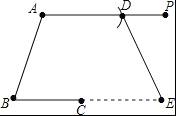
【点评】本题主要考查了直线，射线及线段，解题的关键是利用直线，射线及线段的定义画图．

第166题

“双十一”期间，某电商决定对网上销售的商品一律打8折销售，张燕购买一台某种型号手机时发现，每台手机比打折前少支付500元，求每台该种型号手机打折前的售价．

参考答案：见解析

解析：

【考点】一元一次方程的应用．

【分析】可设每台该种型号手机打折前的售价为x元，根据等量关系：每台手机比打折前少支付500元，列出方程求解即可．

【解答】解：设每台该种型号手机打折前的售价为x元，由题意得：

x﹣0.8x=500，

解得：x=2500．

答：每台该种型号手机打折前的售价为2500元．

【点评】考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．

第167题

某体育用品商场销售某品牌自行车，已知1名熟练工与1名新工人每天共能装配好8辆自行车，3名熟练工与5名新工人每天共能装配好28辆自行车．

①1名新工人每天可以装配好多少辆自行车？

参考答案：见解析

解析：

【考点】一元一次方程的应用．

【分析】①可设一名新工人每天可以装配好x辆自行车，根据等量关系：3名熟练工与5名新工人每天共能装配好28辆自行车，列出方程求解即可；

②解法一：设至少还需要招y名新工人，根据等量关系：该商场预计元旦期间每天可以售出20辆该品牌自行车，列出方程求解即可；

解法二：先求出新工人需要装配好多少辆自行车，再除以2即可求解．

【解答】解：①设一名新工人每天可以装配好x辆自行车，依题意得：

3（8﹣x）+5x=28，

解得：x=2．

答：一名新工人每天可以装配好2辆自行车．

②解法一：设至少还需要招y名新工人，由题意得

（8﹣2）×2+2y=20，

解得：y=4．

答：至少还需要招4名新工人．

解法二：

[20﹣（8﹣2）×2]÷2

=[20﹣6×2]÷2

=[20﹣12]÷2

=8÷2

=4（名）．

答：至少还需要招4名新工人．

【点评】考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．

第168题

如图，已知数轴上点A表示的数为6，点B表示的数为﹣4，C为线段AB的中点，动点P从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．

（1）点C表示的数是　　　　　　；

参考答案：见解析

解析：

【考点】一元一次方程的应用；数轴．

【专题】几何动点问题．

【分析】（1）根据线段中点坐标公式可求点C表示的数；

（2）根据时间=路程÷速度，可求t的值；

（3）根据两点之间的距离公式可求点P表示的数；

（4）分P在点C左边和点C右边两种情况讨论求解；

（5）分点P、Q相遇前和点P、Q相遇后两种情况讨论求解．

【解答】解：（1）（6﹣4）÷2

=2÷2

=1．

故点C表示的数是1．

故答案为：1；

（2）[6﹣（﹣4）]÷2

=10÷2

=5（秒）．

答：当t=5秒时，点P到达点A处．

故答案为：5；

（3）点P表示的数是2t﹣4．

故答案为：2t﹣4；

（4）P在点C左边，

[1﹣2﹣（﹣4）]÷2

=3÷2

=1.5（秒）．

P在点C右边，

[1+2﹣（﹣4）]÷2

=7÷2

=3.5（秒）．

答：当t=1.5秒或3.5秒秒时，线段PC的长为2个单位长度．

故答案为：1.5秒或3.5秒；

（5）点P、Q相遇前，依题意有

（2+1）t=6﹣（﹣4）﹣1，

解得t=3；

点P、Q相遇后，依题意有

（2+1）t=6﹣（﹣4）+1，

解得t=．

答：当t=3秒或秒秒时，PQ的长为1个单位长度．

故答案为：3秒或秒．

【点评】考查了数轴，一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．注意分类思想的应用．

第169题

如果水位升高2m时水位变化记作+2m，那么水位下降3m时水位变化记作（　　）

A.3m

B.﹣3m

C.5m

D.﹣5m

参考答案：B

解析：

【考点】正数和负数．

【分析】首先审清题意，明确“正”和“负”所表示的意义；再根据题意作答．

【解答】解：∵水位升高2m时水位变化记作+2m，

∴水位下降3m时水位变化记作﹣3m．

故选B．

【点评】此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．

第170题

用四舍五入法将3.1416精确到0.01后得到的近似数为（　　）

A.3.1

B.3.14

C.3

D.3.142

参考答案：B

解析：

【考点】近似数和有效数字．

【分析】近似数精确到哪一位，应当看末位数字实际在哪一位．

【解答】解：3.1416精确到0.01为3.14．

故选B．

【点评】本题考查了近似数和有效数字，对于精确到哪一位是需要识记的内容，经常会出错．

第171题

式子x﹣4与x+2互为相反数，则x的值是（　　）

A.0

B.﹣1

C.1

D.2

参考答案：C

解析：

【考点】解一元一次方程．

【专题】计算题；一次方程（组）及应用．

【分析】利用互为相反数两数之和为0列出方程，求出方程的解即可得到x的值．

【解答】解：根据题意得：x﹣4+x+2=0，

移项合并得：2x=2，

解得：x=1．

故选C．

【点评】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．

第172题

下列说法错误的是（　　）

A.直线AB和直线BA是同一条直线

B.射线AB和射线BA是同一条射线

C.线段AB和射线AB都是直线AB的一部分

D.∠ABC和∠CBA是同一个角

参考答案：B

解析：

【考点】直线、射线、线段；角的概念．

【分析】分别利用角的表示方法以及线段、射线、直线的定义得出答案．

【解答】解：A、直线AB和直线BA是同一条直线，正确，不合题意；

B、射线AB和射线BA是同一条射线，错误，符合题意；

C、线段AB和射线AB都是直线AB的一部分，正确，不合题意；

D、∠ABC和∠CBA是同一个角，正确，不合题意；

故选：B．

【点评】此题主要考查了角的表示方法以及线段、射线、直线，正确把握相关定义是解题关键．

第173题

如图，将一副三角尺按不同的位置摆放，下列方式中∠α与∠β互余的是（　　）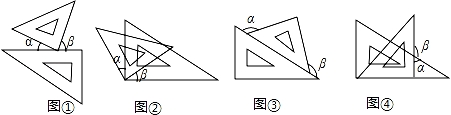

A.图①

B.图②

C.图③

D.图④

参考答案：A

解析：

【考点】余角和补角．

【分析】根据平角的定义，同角的余角相等，等角的补角相等和邻补角的定义对各小题分析判断即可得解．

【解答】解：图①，∠α+∠β=180°﹣90°，互余；

图②，根据同角的余角相等，∠α=∠β；

图③，根据等角的补角相等∠α=∠β；

图④，∠α+∠β=180°，互补．

故选A．

【点评】本题考查了余角和补角，是基础题，熟记概念与性质是解题的关键．

第174题

下列变形正确的是（　　）

A. x=0变形得x=3

B.3x=2x﹣2变形得3x﹣2x=2

C.3x=2变形得x=

D.变形得2x﹣3=3x

参考答案：D

解析：

【考点】等式的性质．

【分析】根据等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．

【解答】解：A、两边都乘以3，得x=0，故A错误；

B、左边减2x，右边加（4﹣2x），故B错误；

C、左边除以3，右边除以，故C错误；

D、两边都乘以3，故D正确；

故选：D．

【点评】本题主要考查了等式的基本性质，等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．

第175题

下列图形可以作为一个正方体的展开图的是（　　）

A.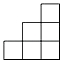

B.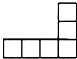

C.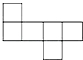

D.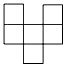

参考答案：C

解析：

【考点】几何体的展开图．

【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．

【解答】解：A、不能作为一个正方体的展开图，故本选项错误；

B、不能作为一个正方体的展开图，故本选项错误；

C、能作为一个正方体的展开图，故本选项正确；

D、不能作为一个正方体的展开图，故本选项错误；

故选C．

【点评】本题考查了几何体的展开图，属于基础题，注意培养自己的空间想象能力．

第176题

把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本，设这个班有学生x人，下列方程正确的是（　　）

A.3x+20=4x﹣25

B.3x﹣25=4x+20

C.4x﹣3x=25﹣20

D.3x﹣20=4x+25

参考答案：A

解析：

【考点】由实际问题抽象出一元一次方程．

【分析】设这个班有学生x人，等量关系为图书的数量是定值，据此列方程．

【解答】解：设这个班有学生x人，

由题意得，3x+20=4x﹣25．

故选A．

【点评】本题考查了由实际问题抽象出一元一次方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列出方程．

第177题

如图，点C是线段AB的中点，点D是线段BC上一点，下列条件不能确定点D是线段BC的中点的是（　　）

A.CD=DB

B.BD=AD

C.BD=AB﹣AD

D.2AD=3BC

参考答案：C

解析：

【考点】两点间的距离．

【分析】根据线段中点的定义，结合图形判断即可．

【解答】解：∵CD=DB，

∴点D是线段BC的中点，A不合题意；

∵点C是线段AB的中点，

∴AC=BC，又BD=AD，

∴点D是线段BC的中点，B不合题意；

BD=AB﹣AD，不能确定点D是线段BC的中点，C符合题意；

∵点C是线段AB的中点，

∴AC=BC，2AD=3BC，

∴2（BC+CD）=3BC，

∴BC=2CD，

∴点D是线段BC的中点，D不合题意，

故选：C．

【点评】本题考查的是两点间的距离的计算，掌握线段中点的定义、灵活运用数形结合思想是解题的关键．

第178题

下列结论：

①若关于x的方程ax+b=0（a≠0）的解是x=1，则a+b=0；

A.①②

B.②③

C.①③

D.①②③

参考答案：C

解析：

【考点】一元一次方程的解．

【分析】根据方程的解的定义即可判断．

【解答】解：①把x=1代入方程得a+b=0，故结论正确；

②方程ax+b=0（a≠0）移项，得ax=﹣b，

两边同时除以a得x=﹣，

∵b=2a，

∴=2，

∴x=﹣2，

故命题错误；

③把x=1代入方程ax+b=1一定有a+b=1成立，则x=1是方程的解．

故选C．

【点评】本题考查了方程的解的定义，方程的解就是能使方程左右两边相等的未知数的值，理解定义是关键．

第179题

单项式﹣2ab²的系数是　　．

参考答案：﹣2

解析：

【考点】单项式．

【分析】单项式的系数就是所含字母前面的数字，由此即可求解．

【解答】解：单项式﹣2ab²的系数是﹣2，

故答案为﹣2．

【点评】此题主要考查了单项式 的系数的定义，解题的关键是熟练掌握相关的定义即可求解．

第180题

比较：28°15′　　28.15°（填“＞”、“＜”或“=”）．

参考答案：＞

解析：

【考点】角的大小比较；度分秒的换算．

【分析】首先利用度分秒换算法则进行转化，再比较大小．

【解答】解：∵28°15′=28°+（15÷60）°=28.25°，

∴28°15′＞28.15°．

故答案为：＞．

【点评】此题主要考查了角的比较大小以及度分秒转化，正确掌握度分秒转化是解题关键．