第181题

如图，把原来弯曲的河道改直，A、B两地间的河道长度就发生了变化，请你用数学知识解释这一现象产生的原因　　．

参考答案：两点之间线段最短

解析：

【考点】线段的性质：两点之间线段最短．

【专题】应用题．

【分析】直接利用线段的性质得出答案．

【解答】解：把原来弯曲的河道改直，A、B两地间的河道长度就发生了变化，

用数学知识解释这一现象产生的原因：两点之间线段最短．

故答案为：两点之间线段最短．

【点评】此题主要考查了线段的性质，正确把握线段的性质是解题关键．

第182题

点A，B，C在同一条直线上，AB=3cm，BC=1cm，则AC=　　．

参考答案：2cm或4cm

解析：

【考点】两点间的距离．

【分析】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系的多种可能，再根据题意画出的图形进行解答．

【解答】解：本题有两种情形：

（1）当点C在线段AB上时，如图，AC=AB﹣BC，

又∵AB=3cm，BC=1cm，

∴AC=3﹣1=2cm；

（2）当点C在线段AB的延长线上时，如图，AC=AB+BC，

又∵AB=3cm，BC=1cm，∴AC=3+1=4cm．

故线段AC=2cm或4cm．

故答案为：2cm或4cm．

【点评】考查了两点间的距离，在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．

第183题

一件商品提价25%后发现销路不是很好，若恢复原价，则应降价　　%．

参考答案：20

解析：

【考点】有理数的混合运算．

【专题】计算题．

【分析】设原价为1，降价x%，由于提价25%后则销售为1•（1+25%），然后把它降价x%得到销售价为1，所以1•（1+25%）•（1﹣x%）=1，然后解此方程即可．

【解答】解：设原价为1，降价x%，

根据题意得1•（1+25%）•（1﹣x%）=1，

1﹣x%=1×，

所以x=20．

故答案为20．

【点评】本题考查了实数的运算：先算乘方，再算乘除，然后进行加减运算；有括号先算括号．

第184题

如图，数轴上的有理数a，b满足|3a﹣b|﹣|a+2b|=|a|，则=　　．

参考答案：-1/3

解析：

【考点】绝对值；数轴．

【分析】根据点a、b在数轴上的位置可判断出3a﹣b＜0，a+2b＞，a＜0，然后化简绝对值，从而可求得答案．

【解答】解：∵由题意可知：3a﹣b＜0，a+2b＞0，a＜0，

∴b﹣3a﹣（a+2b）=﹣a．

整理得：﹣b=3a．

∴．

故答案为：﹣．

【点评】本题主要考查的是绝对值的化简、数轴的认识，根据a、b在数轴上的位置，判断出3a﹣b＜0，a+2b＞，a＜0是解题的关键．

第185题

计算：

（1）3×（﹣4）+18÷（﹣6）

参考答案：见解析

解析：

【考点】有理数的混合运算．

【专题】计算题．

【分析】（1）根据有理数的运算法则，先算乘除，然后计算加减，即可得出结果．

（2）根据有理数的运算法则先算乘方，然后计算乘除，最后求和即可得出答案．

【解答】解：（1）3×（﹣4）+18÷（﹣6）

=﹣12+（﹣3）

=﹣15；

（2）（﹣2）²×5+（﹣2）³÷4

=4×5+（﹣8）÷4

=20+（﹣2）

=18．

【点评】题目考查了有理数的混合运算，解决此类问题的关键是掌握有理数混合运算的法则，题目整体较为简单，适合随堂训练．

第186题

解方程

（1）5x=2（x+3）

参考答案：见解析

解析：

【考点】解一元一次方程．

【专题】计算题；一次方程（组）及应用．

【分析】（1）方程去括号，移项合并，把x系数化为1，即可求出解；

（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．

【解答】解：（1）去括号，得：5x=2x+6，

移项合并得：3x=6，

解得：x=2；       

（2）去分母，得2x﹣4=3x，

移项合并得：x=﹣4．

【点评】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．

第187题

先化简，再求值：a﹣2（a﹣b²）+（﹣a+b²），其中a=﹣2，b=1．

参考答案：见解析

解析：

【考点】整式的加减—化简求值．

【专题】计算题；整式．

【分析】原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．

【解答】解：原式=a﹣2a+2b²﹣a+b²=﹣2a+3b²，

当a=﹣2，b=1时，原式=4+3=7．

【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．

第188题

如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．

（1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；

参考答案：见解析

解析：

【考点】方向角．

【分析】（1）根据方向角的度数，可得答案；

（2）根据余角与补角的关系，可得∠AOD的度数，根据角的和差，可得方向角．

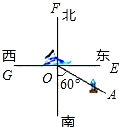
【解答】解：（1）如图1：

，

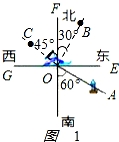（2）如图2：

，

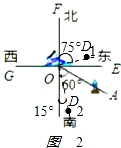由∠AOD的补角是它的余角的3倍，得

180°﹣∠AOD=3（180°﹣∠AOD）．

解得∠AOD=45°．

故D在O南偏东15°或北偏东75°．

故答案为：D在O南偏东15°或北偏东75°．

【点评】本题考查了方向角，利用余角与补角的关系得出∠AOD的度数是解题关键．

第189题

如图，延长线段AB至点C，使BC=AB，反向延长AB至D，使AD=AB．

（1）依题意画出图形，则=　　　　　　（直接写出结果）；

参考答案：见解析

解析：

【考点】两点间的距离．

【分析】（1）先根据题意画出图形，然后计算BC与AD的比值即可；

（2）由线段中点的定义可知2BE=BC=，然后根据BD﹣2BE=10列方程求解即可．

【解答】解：（1）如图1所示：

∵BC=AB，AD=AB，

∴==．

故答案为：．

（2）如图2所示：

∵E是BC的中点，

∴BC=2BE=．

∵BD﹣2BE=10，

∴+AB﹣=10．

解得：AB=12．

【点评】本题主要考查的是两点间的距离，根据题意列出关于AB的方程是解题的关键．

第190题

某市近期公布的居民用天然气阶梯价格听证会方案如下：

参考答案：见解析

解析：

【考点】一元一次方程的应用；有理数的混合运算．

【专题】计算题；开放型；方程思想；一次方程（组）及应用．

【分析】（1）依题意可知，小明家天然气用量在第二档，列算式计算可得；

（2）依题意可知，小红家天然气用量在第三档，列算式计算可得；

（3）根据（2）计算结果可知，该户天然气用量属第三档，列方程求解可得．

【解答】解：（1）根据题意可知，若小明家2015年使用天然气500立方米，

则需缴纳天然气费为：2.53×360+2.78×（500﹣360）=1300（元）；

（2）若小红家2015年使用天然气650立方米，

则小红家2015年需缴纳的天然气费为：2.53×360+2.78×（600﹣360）+3.54×（650﹣600）=1755（元）；

答：小红家2015年需缴纳的天然气费为1755元．

（3）∵2286元＞1755元，该用户2015年使用天然气超过600立方米，

设该用户2015年使用天然气x立方米，依题意得：

2.53×360+240×2.78+3.54×（x﹣600）=2286，

解得x=800

答：该户2015年使用天然气800立方米．

故答案为：（1）1300．

【点评】本题考查了一元一次方程的应用的知识，解答此类题目确定费用档位是关键，属基础题．

第191题

如图，已知∠AOB=120°，射线OA绕点O以每秒钟6°的速度逆时针旋转到OP，设射线OA旋转OP所用时间为t秒（t＜30）．

（1）如图1，直接写出∠BOP=　　°（用含t的式子表示）；

参考答案：见解析

解析：

【考点】角的计算；角平分线的定义．

【分析】（1）由于∠AOB=120°，∠AOP=6t，即可得到∠BOP=（120﹣6t）°；

（2）根据角平分线的定义得到∠MOP=∠AOP=3t，∠NOP=∠BOP=60﹣3t，根据线段的和差即可得到结论；

（3）根据角平分线的定义得到∠MOA=∠MOP=∠AOP=3t，∠BON=∠NOP=∠BOP=3t﹣60，根据已知条件列方程即可得到结论．

【解答】解：（1）∵∠AOB=120°，∠AOP=6t，

∴∠BOP=（120﹣6t）°．

故答案为：（120﹣6t）；

（2）∵OM平分∠AOP，ON平分∠BOP，

∴∠MOP=∠AOP=3t，∠NOP=∠BOP=60﹣3t，

∴∠MON=∠MOP+∠NOP=3t+60﹣3t=60°；

（3）∵OM平分∠AOP，ON平分∠BOP，

∴∠MOA=∠MOP=∠AOP=3t，

∠BON=∠NOP=∠BOP=3t﹣60，

∵2∠BOM=3∠BON，

即2（120﹣3t）=3（3t﹣60），

解得t=28．

【点评】此题考查了角的计算，读懂题目信息，准确识图并表示出相关的角度，然后列出方程是解题的关键．

第192题

数轴上有A、B两点，A在B的左侧，已知点B对应的数为2，点A对应的数为a．

（1）若a=﹣3，则线段AB的长为　　（直接写出结果）；

参考答案：见解析

解析：

【考点】一元一次方程的应用；数轴．

【分析】（1）根据两点间的距离求解；

（2）设C点对应的数为x，则AC=x﹣a，BC=2﹣x，根据AC﹣BC=2列出关于x的方程并求解；

（3）根据题意得到AC=x﹣a=2+﹣a，AD=AC=1﹣，结合（2）的已知条件AC﹣BC=2和图示中的BD=AB+AD列出关于a的方程﹣2a=2﹣a+1﹣，并解方程．

【解答】解：（1）若a=﹣3时，则点A对应的数是﹣3，所以AB=2﹣（﹣3）=5，即线段AB的长度为5；

故答案是：5；

（2）设C点对应的数为x，则AC=x﹣a，BC=2﹣x，

∵AC﹣BC=2，即（x﹣a）﹣（2﹣x）=2，

解得x=2+，即点C表示的数为2+；           

（3）依题意AC=x﹣a=2+﹣a=2﹣，

AD=AC=（2﹣）=1﹣，

∵AB=2﹣a，

又BD=AB+AD，即﹣2a=2﹣a+1﹣，

解得 a=﹣4．

【点评】本题考查了数轴和一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．

第193题

﹣3的绝对值是（　　）

A.3

B.﹣3

C.

D.

参考答案：A

解析：

【考点】绝对值．

【分析】根据一个负数的绝对值等于它的相反数得出．

【解答】解：|﹣3|=﹣（﹣3）=3．

故选：A．

【点评】考查绝对值的概念和求法．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．

第194题

在﹣2，0，2，﹣3这四个数中，最小的数是（　　）

A.2

B.0

C.﹣2

D.﹣3

参考答案：D

解析：

【考点】有理数大小比较．

【专题】计算题．

【分析】根据有理数的大小比较法则（正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小比较即可．

【解答】解：∵﹣3＜﹣2＜0＜2，

∴最小的数是﹣3，

故选D．

【点评】本题考查了有理数的大小比较法则，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．

第195题

2015年3月29日，习近平主席同出席博鳌亚洲论坛年会的中外企业家代表座谈时说：通过“一带一路”，我们希望用10年左右的时间，使中国同沿线国家的年贸易额突破2.5万亿美元．2.5万亿用科学记数法表示为（　　）

A.2.5×10⁴

B.2.5×10⁸

C.2.5×10¹²

D.25×10¹¹

参考答案：C

解析：

【考点】科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【解答】解：将2.5万亿用科学记数法表示为：2.5×10¹²．

故选：C．

【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

第196题

下列运算中结果正确的是（　　）

A.3a+2b=5ab

B.5y﹣3y=2

C.﹣3x+5x=﹣8x

D.3x²y﹣2x²y=x²y

参考答案：D

解析：

【考点】合并同类项．

【分析】①所含字母相同，并且相同字母的指数相同，像这样的项是同类项；②合并同类项，系数相加字母不变；③、④合并同类项，系数相加字母和字母的指数不变．

【解答】解：A、算式中所含字母不同，所以不能合并，故A错误；

B、5y﹣3y=2y，合并同类项，系数相加字母不变，故B错误；

C、﹣3x+5x=2x，合并同类项，系数相加减，故C错误；

D、3x²y﹣2x²y=x²y，合并同类项，系数相加字母和字母的指数不变，故D正确．

故选D．

【点评】“同类项的概念是所含字母相同，相同字母的指数也相同的项是同类项，不是同类项的一定不能合并”这是本题特别应该注意的地方．

第197题

在下列调查中，适宜采用全面调查的是（　　）

A.了解我省中学生的视力情况

B.了解七（1）班学生校服的尺码情况

C.检测一批电灯泡的使用寿命

D.调查安徽卫视《第一时间》栏目的收视率

参考答案：B

解析：

【考点】全面调查与抽样调查．

【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．

【解答】解：A、了解我省中学生的视力情况，调查范围广，适合抽样调查，故A错误；

B、了解七（1）班学生校服的尺码情况，适合普查，故B正确；

C、检测一批电灯泡的使用寿命，调查具有破坏性，适合抽样调查，故C错误；

D、调查安徽卫视《第一时间》栏目的收视率，调查范围广，适合抽样调查，故D错误；

故选：B．

【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

第198题

有理数a、b在数轴上的位置如图所示，下列各式成立的是（　　）

A.a+b＞0

B.a﹣b＞0

C.ab＞0

D.

参考答案：D

解析：

【考点】有理数大小比较；数轴．

【分析】根据各点在数轴上的位置判断出a，b的取值范围，进而可得出结论．

【解答】解：∵由图可知，a＜﹣1＜0＜b＜1，

∴a+b＜0，故A错误；

a﹣b＜0，故B错误；

ab＜0，故C错误；

＜0，故D正确．

故选D．

【点评】本题考查的是有理数的大小比较，熟知数轴的特点是解答此题的关键．

第199题

已知a，b满足方程组，则a+b的值为（　　）

A.﹣4

B.4

C.﹣2

D.2

参考答案：B

解析：

【考点】解二元一次方程组．

【专题】计算题．

【分析】求出方程组的解得到a与b的值，即可确定出a+b的值．

【解答】解：，

①+②×5得：16a=32，即a=2，

把a=2代入①得：b=2，

则a+b=4，

故选B．

【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

第200题

如图，C、D是线段AB上两点，若CD=4cm，DB=7cm，且B是AC的中点，则AC的长等于（　　）

A.3cm

B.6cm

C.11cm

D.14cm

参考答案：B

解析：

【考点】两点间的距离．

【分析】根据线段的和差，可得BC的长，根据线段中点的性质，可得答案．

【解答】解：由线段的和差，得

BC=BD﹣CD=7﹣4=3cm．

由B是AC的中点，得

AC=2BC=2×3=6cm，

故选：B．

【点评】本题考查了两点间的距离，利用线段的和差得出BC的长是解题关键．