第201题

如图，将4×3的网格图剪去5个小正方形后，图中还剩下7个小正方形，为了使余下的部分（小正方形之间至少要有一条边相连）恰好能折成一个正方体，需要再剪去1个小正方形，则应剪去的小正方形的编号是（　　）

A.7

B.6

C.5

D.4

参考答案：C

解析：

【考点】展开图折叠成几何体．

【分析】由平面图形的折叠及正方体的表面展开图的特点解题．注意只要有“田”字格的展开图都不是正方体的表面展开图．

【解答】解：根据只要有“田”字格的展开图都不是正方体的表面展开图，应剪去的小正方形的编号是5．

故选C．

【点评】本题考查了展开图折叠成几何体，解题时勿忘记正方体展开图的各种情形．

第202题

找出以下图形变化的规律，则第2016个图形中黑色正方形的数量是（　　）

A.3021

B.3022

C.3023

D.3024

参考答案：D

解析：

【考点】规律型：图形的变化类．

【专题】规律型．

【分析】观察图形，得到第2016个图形中小正方形的个数，即可确定出黑色正方形的数量．

【解答】解：根据题意得：第2016个图形中正方形的个数为2×2016=4032（个），

空白正方形的规律为：0，1，1，2，2，3，3，…，

∵÷2=2015÷2=1007…1，

∴空白正方形个数为1008，

则第2016个图形中黑色正方形的数量是4032﹣1008=3024，

故选D．

【点评】此题考查了规律型：图形的变化类，弄清题中的规律是解本题的关键．

第203题

2的相反数是　　．

参考答案：﹣2

解析：

【考点】相反数．

【分析】根据相反数的定义可知．

【解答】解：﹣2的相反数是2．

【点评】主要考查相反数的定义：只有符号相反的两个数互为相反数．0的相反数是其本身．

第204题

试写出一个解为x=1的一元一次方程：　　．

参考答案：x﹣1=0

解析：

【考点】一元一次方程的解．

【专题】开放型．

【分析】只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程；它的一般形式是ax+b=0（a，b是常数且a≠0）；根据题意，写一个符合条件的方程即可．

【解答】解：∵x=1，

∴根据一元一次方程的基本形式ax+b=0可列方程：x﹣1=0．（答案不唯一）

【点评】本题是一道简单的开放性题目，考查学生的自己处理问题的能力．

第205题

某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为　　名．

参考答案：60

解析：

【考点】扇形统计图．

【分析】设被调查的总人数是x人，根据最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，即可列方程求解．

【解答】解：设被调查的总人数是x人，则40%x﹣30%x=6，

解得：x=60．

故答案是：60．

【点评】本题考查的是扇形统计图的综合运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比大小．

第206题

如果∠α和∠β互补，且∠α＞∠β，则下列表示角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．能表示∠β的余角的是　　（填写序号）

参考答案：①②④

解析：

【考点】余角和补角．

【专题】常规题型．

【分析】互补即两角的和为180°，互余即两角的和为90°，根据这一条件判断即可．

【解答】解：已知∠β的余角为：90°﹣∠β，故①正确；

∵∠α和∠β互补，且∠α＞∠β，

∴∠α+∠β=180°，∠α＞90°，

∴∠β=180°﹣∠α，

∴∠β的余角为：90°﹣（180°﹣∠α）=∠α﹣90°，故②正确；

∵∠α+∠β=180°，

∴（∠α+∠β）=90°，

∴∠β的余角为：90°﹣∠β=（∠α+∠β）﹣∠β=（∠α﹣∠β），故④正确．

故答案为：①②④．

【点评】本题考查了余角和补角的定义，牢记定义是关键．

第207题

计算：﹣1²+3×（﹣2）³﹣（﹣6）÷（﹣）²．

参考答案：见解析

解析：

【考点】有理数的混合运算．

【专题】计算题；实数．

【分析】原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．

【解答】解：原式=﹣1﹣24+54=29．

【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

第208题

解方程：2﹣=

参考答案：见解析

解析：

【考点】解一元一次方程．

【分析】先去分母，再去括号、移项、合并同类项、系数化为1即可．

【解答】解：去分母得，12﹣2（2x+1）=3（1+x），

去括号得，12﹣4x﹣2=3+3x，

移项得，﹣4x﹣3x=3﹣12+2，

合并同类项得，﹣7x=﹣7，

系数化为1得，x=1．

【点评】本题考查的是解一元一次方程，熟知解一元一次方程的一般步骤是解答此题的关键．

第209题

如图，∠AOB=∠COD=90°，OC平分∠AOB，∠BOD=3∠DOE．试求∠COE的度数．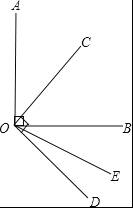

参考答案：见解析

解析：

【考点】角平分线的定义．

【专题】计算题．

【分析】根据角平分线的定义先求∠BOC的度数，即可求得∠BOD，再由∠BOD=3∠DOE，求得∠BOE．

【解答】解：∵∠AOB=90°，OC平分∠AOB

∴∠BOC=∠AOB=45°

∵∠BOD=∠COD﹣∠BOC=90°﹣45°=45°

∠BOD=3∠DOE

∴∠DOE=15°

∴∠COE=∠COD﹣∠DOE=90°﹣15°=75°

故答案为75°．

【点评】本题主要考查角平分线的定义，根据角平分线定义得出所求角与已知角的关系转化求解．

第210题

解方程组．

参考答案：见解析

解析：

【考点】解二元一次方程组．

【专题】计算题；一次方程（组）及应用．

【分析】方程组利用加减消元法求出解即可．

【解答】解：，

①×2+②得：5x=5，即x=1，

把x=1代入①得：y=1，

则方程组的解为．

【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

第211题

老师在黑板上书写了一个正确的演算过程，随后用一张纸挡住了一个二次三项式，形式如下：﹣3x=x²﹣5x+1

（1）求所挡的二次三项式；

参考答案：见解析

解析：

【考点】整式的加减；代数式求值．

【分析】（1）直接移项即可得出结论；

（2）把x=﹣1代入（1）中的二次三项式进行计算即可．

【解答】解：（1）所挡的二次三项式=x²﹣5x+1+3x=x²﹣2x+1；

（2）当x=﹣1时，原式=1+2+1=4．

【点评】本题考查的是整式的加减，熟知整式的加减实质上就是合并同类项是解答此题的关键．

第212题

已知一道路沿途5个车站A、B、C、D、E，它们之间的距离如图所示（km）

参考答案：见解析

解析：

【考点】两点间的距离．

【分析】（1）根据线段的和差，可得答案；

（2）根据线段中点的性质，可得关于b的方程，根据解方程，可得答案．

【解答】解：（1）由线段的和差，得

DE=CE﹣CD=（3a﹣b）﹣（2a﹣3b）=a+2b；

D、E两站之间的距离是a+2b；

（2）D为线段AE的中点，得

AD=DE，即a+b+2a﹣3b=a+2b，

a=2b=8，

b=4．

【点评】本题考查了两点间的距离，利用线段中点的性质得出关于b的方程式解题关键．

第213题

为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：

某校被调查学生选择社团意向统计表

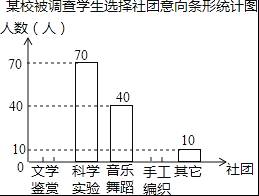
参考答案：见解析

解析：

【考点】条形统计图；用样本估计总体；统计表．

【分析】（1）根据选择科学实验的人数是70人，所占的百分比是35%，即可求得调查的总人数，进而根据百分比的意义求解；

（2）根据百分比的意义求得选择文学欣赏和手工纺织的人数，即可补全直方图；

（3）利用总人数乘以对应的百分比即可求解．

【解答】解：（1）本次调查的学生总人数是70÷35%=200（人），

b==20%，

c==5%，

a=1﹣35%﹣20%﹣10%﹣5%=30%；

（2）选择文学欣赏的人数是：200×30%=60（人），

选择手工纺织的人数是：200×10%=20（人），

；

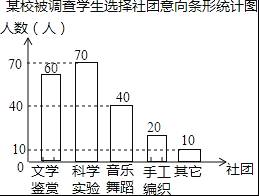（3）该校共有1200名学生，估计全校选择“科学实验”社团的人数是1200×35%=420（人）．

【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．

第214题

为实现教育均衡发展，打造新优质学校，瑶海区计划对A、B两类薄弱学校全部进行改造，根据预算，共需资金1575万元．改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元，求改造一所A类学校和一所B类学校所需的资金分别是多少万元？

参考答案：见解析

解析：

【考点】二元一次方程组的应用．

【分析】设改造一所A类学校所需资金为x万元，改造一所B类学校所需的资金是y万元，根据改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元，列方程组求解．

【解答】解：设改造一所A类学校所需资金为x万元，改造一所B类学校所需的资金是y万元，

由题意得，，

解得：．

答：改造一所A类学校所需资金为60万元，改造一所B类学校所需的资金是85万元．

【点评】本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组求解．

第215题

观察图形，解答问题：

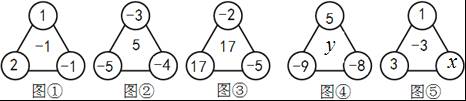
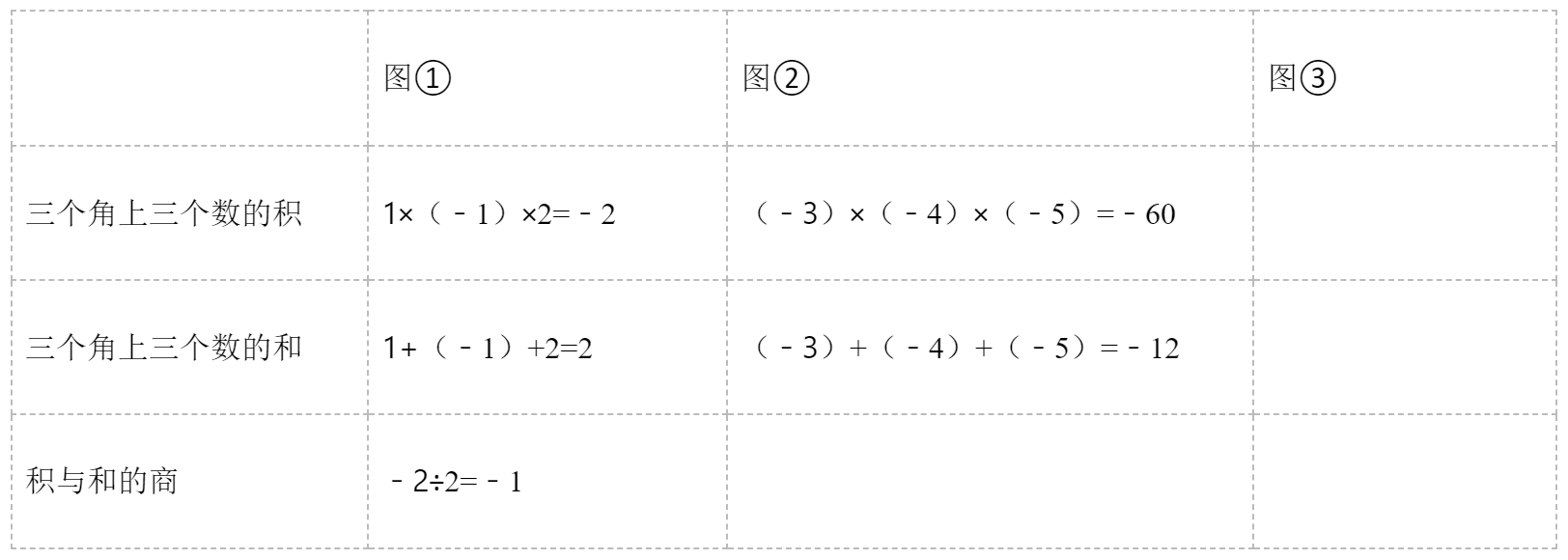
参考答案：见解析

解析：

【考点】规律型：数字的变化类．

【专题】压轴题．

【分析】（1）根据图形和表中已填写的形式，即可求出表中的空格；

（2）根据图①②③可知，中间的数是三个角上的数字的乘积与和的商，列出方程，即可求出x、y的值．

【解答】解：（1）图②：（﹣60）÷（﹣12）=5，

图③：（﹣2）×（﹣5）×17=170，

（﹣2）+（﹣5）+17=10，

170÷10=17．

（2）图④：5×（﹣8）×（﹣9）=360，

5+（﹣8）+（﹣9）=﹣12，

y=360÷（﹣12）=﹣30，

图⑤：=﹣3，

解得x=﹣2；

经检验x=﹣2是原方程的根，

∴图⑤中的数为﹣2．

【点评】此题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力．

第216题

﹣2的倒数是（　　）

A．﹣ B． C．﹣2 D．2

A.﹣

B.

C.﹣2

D.2

参考答案：A

解析：

【考点】倒数．

【专题】常规题型．

【分析】根据倒数的定义即可求解．

【解答】解：﹣2的倒数是﹣．

故选：A．

【点评】主要考查倒数的概念及性质．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．

第217题

阿里巴巴数据显示，2015年天猫商城“双11”全球狂欢交易额超912亿元，数据912亿用科学记数法表示为（　　）

A.912×10⁸

B.91.2×10⁹

C.9.12×10¹⁰

D.0.912×10¹⁰

参考答案：C

解析：

【考点】科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于912亿有11位，所以可以确定n=11﹣1=10．

【解答】解：912亿=912000 000 000=9.12×10¹⁰．

故选C．

【点评】此题考查科学记数法表示较大的数的方法，准确确定n值是关键．

第218题

下列调查中，其中适合采用抽样调查的是（　　）

①检测深圳的空气质量；

A.①

B.②

C.③

D.④

参考答案：A

解析：

【考点】全面调查与抽样调查．

【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．

【解答】解：①检测深圳的空气质量，应采用抽样调查；

②为了解某中东呼吸综合征（MERS）确诊病人同一架飞机乘客的健康情况，意义重大，应采用全面调查；

③为保证“神舟9号”成功发射，对其零部件进行检查，意义重大，应采用全面调查；

④调查某班50名同学的视力情况，人数较少，应采用全面调查，

故选：A．

【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

第219题

下列几何体中，从正面看（主视图）是长方形的是（　　）

A.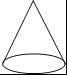

B.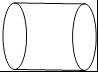

C.

D.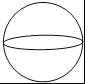

参考答案：B

解析：

【考点】简单几何体的三视图．

【分析】主视图是分别从物体正面看，所得到的图形．

【解答】解：圆锥的主视图是等腰三角形，

圆柱的主视图是长方形，

圆台的主视图是梯形，

球的主视图是圆形，

故选B．

【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．

第220题

下列运算中，正确的是（　　）

A.﹣2﹣1=﹣1

B.﹣2（x﹣3y）=﹣2x+3y

C.

D.5x²﹣2x²=3x²

参考答案：D

解析：

【考点】有理数的混合运算；合并同类项；去括号与添括号．

【分析】计算出各选项中式子的值，即可判断哪个选项是正确的．

【解答】解：因为﹣2﹣1=﹣3，﹣2（x﹣3y）=﹣2x+6y，2÷6×=2×，5x²﹣2x²=3x²，

故选D．

【点评】本题考查有理数混合运、合并同类项、去括号与添括号，解题的关键是明确它们各自的计算方法．