第61题

已知x+y=10，xy=16，则x²y+xy²的值为　　．

参考答案：160

解析：

【分析】首先提取公因式xy，进而将已知代入求出即可．

【解答】解：∵x+y=10，xy=16，

∴x²y+xy²=xy（x+y）=10×16=160．

故答案为：160．

【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．

第62题

当x=　　时，分式的值为0．

参考答案：﹣1

解析：

【分析】分式的值为0的条件是：（1）分子=0；（2）分母≠0．两个条件需同时具备，缺一不可．据此可以解答本题．

【解答】解：由题意可得x+1=0且x﹣1≠0，

解得x=﹣1．

故答案为﹣1．

【点评】由于该类型的题易忽略分母不为0这个条件，所以常以这个知识点来命题．

第63题

如图，在△ABC中，∠A=75°，∠B=30°，则∠ACD=　　．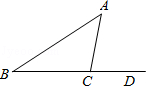

参考答案：105°

解析：

【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．

【解答】解：由三角形的外角性质得，∠ACD=∠A+∠B=75°+30°=105°．

故答案为：105°．

【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，是基础题，熟记性质是解题的关键．

第64题

如图，△ABC的周长为19cm，AC的垂直平分线DE交AC于点E，E为垂足，AE=3cm，则△ABD的周长为　　．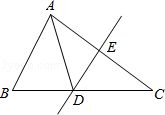

参考答案：13cm

解析：

【分析】根据垂直平分线的性质计算．△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC．

【解答】解：∵AC的垂直平分线DE交BC于D，E为垂足

∴AD=DC，AC=2AE=6cm，

∵△ABC的周长为19cm，

∴AB+BC=13cm

∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm．

故答案为：13cm．

【点评】本题考查了线段垂直平分线的性质；解决本题的关键是利用线段的垂直平分线性质得到相应线段相等．

第65题

如图，在△ABC和△ABD中，∠C=∠D=90°，若利用“HL”证明△ABC≌△ABD，则需要加条件　　或　　．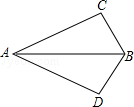

参考答案：BC=BD或AC=AD

解析：

【分析】本题要判定△ABC≌△ABD，已知∠C=∠D=90°，AB=AB，具备了一组边、一组角相等，故添加∠CAB=∠DAB或∠CBA=∠DBA，BD=BC或AD=AC后可分别根据AAS、HL判定三角形全等．

【解答】解：添加∠CAB=∠DAB或∠CBA=∠DBA，BD=BC或AD=AC．

∵∠C=∠D，∠CAB=∠DAB（∠CBA=∠DBA），AB=AB

∴△ABC≌△ABD（AAS）；

∵∠C=∠D=90°，AB=AB（AD=AC），BD=BC

∴△ABC≌△ABD（HL）．

故答案为BC=BD或AC=AD．

【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

第66题

如图所示，要测量河两岸相对的两点A、B的距离，在AB的垂线BF上取两点C、D，使BC=CD，过D作BF的垂线DE，与AC的延长线交于点E，则∠ABC=∠CDE=90°，BC=DC，∠1=　　，△ABC≌　　，若测得DE的长为25米，则河宽AB长为　　．

参考答案：∠2，△EDC，25米

解析：

【分析】已知直角三角形中，一锐角相等，又有一直角边相等，所以可得到其全等，然后由全等的性质得到何宽AB的长度．

【解答】解：∵CD=BD，∠1=∠2，∠ABC=∠CDE=90°，

∴Rt△ABC≌Rt△EDC，

∴AB=DE，

∴AB=25米

故填∠2，△EDC，25米．

【点评】本题考查了全等三角形的应用；认真观察图形，找出已知条件，把实际问题转化为数学问题解决是正确解答本题的关键．

第67题

在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x⁴﹣y⁴，因式分解的结果是（x﹣y）（x+y）（x²+y²），若取x=9，y=9时，则各个因式的值是：（x﹣y）=0，（x+y）=18，（x²+y²）=162，于是就可以把“018162”作为一个六位数的密码．对于多项式4x³﹣xy²，取x=10，y=10时，用上述方法产生的密码是：　　（写出一个即可）．

参考答案：101030或103010或301010

解析：

【分析】把所求的代数式分解因式后整理成条件中所给出的代数式的形式，然后整体代入即可．

【解答】解：4x³﹣xy²=x（4x²﹣y²）=x（2x+y）（2x﹣y），

当x=10，y=10时，x=10；2x+y=30；2x﹣y=10，

用上述方法产生的密码是：101030或103010或301010．

故答案为：101030或103010或301010．

【点评】本题考查了提公因式法，公式法分解因式，读懂题目信息，正确进行因式分解是解题的关键，还考查了代数式求值的方法，同时还隐含了整体的数学思想和正确运算的能力．

第68题

（1）计算：112²﹣113×111．

（2）解方程：=．

参考答案：见解析

解析：

【分析】（1）原式变形后，利用平方差公式计算即可得到结果．

（2）通过去分母，移项、合并同类项以及化系数为1进行解答；

【解答】解：（1）原式=112²﹣（112+1）×（112﹣1）=112²﹣（112²﹣1）=112²﹣112²+1=1．

（2）分式方程两边乘以（x+2）（x﹣2）得，

3（x+2）=x﹣2，

x=﹣4．

检验，当x=﹣4时，（x+2）（x﹣2）≠0

所以原分式方程的解是x=﹣4．

【点评】此题考查了解分式方程、平方差公式，熟练掌握平方差公式是解本题的关键．

第69题

先化简，再求值：（2x+y）（2x﹣y）﹣3（2x﹣y）²，其中x=1，y=﹣2．

参考答案：见解析

解析：

【分析】原式利用平方差公式，以及完全平方公式化简，去括号合并得到最简结果，把x与y的值代入计算即可求出值．

【解答】解：原式=4x²﹣y²﹣3（4x²﹣4xy+y²）=4x²﹣y²﹣12x²+12xy﹣3y²=﹣8x²+12xy﹣4y²，

当x=1，y=﹣2时，原式=﹣8﹣24﹣16=﹣48．

【点评】此题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解本题的关键．

第70题

如图，在△ABC中，∠B=42°，∠C=78°，AD平分∠BAC．

（1）求∠ADC的度数；

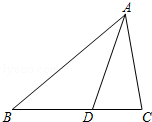
参考答案：见解析

解析：

【分析】（1）根据三角形的内角和得到∠BAC=180°﹣∠B﹣∠C=60°，由角平分线的性质得到∠BAD=∠BAC=30°，根据三角形的外角的想自己看得到结论；

（2）过A作AE⊥BC于E，根据垂直的定义得到∠AEB=90°，根据三角形的外角的性质即可得到结论．

【解答】（1）∵∠B=42°，∠C=78°，

∴∠BAC=180°﹣∠B﹣∠C=60°，

∵AD平分∠BAC，

∴∠BAD=∠BAC=30°，

∴∠ADC=∠B+∠BAD=42°+30°=72°；

（2）如图所示，过A作AE⊥BC于E，

∴∠AEB=90°，

∴∠DAE=180°﹣∠AED﹣∠ADE=180°﹣90°﹣72°=18°．

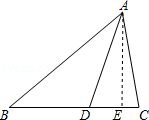
【点评】本题考查了三角形的内角和，角平分线的定义，熟记三角形的内角和是解题的关键．

第71题

如图，已知AD⊥AB，BC⊥AB，AC与BD交于点O，AD=BC．求证：

（1）△ABC≌△BAD．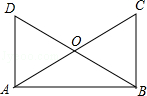

参考答案：见解析

解析：

【分析】（1）根据垂直得：∠DAB=∠ABC=90°，所以根据SAS证明△ABC≌△BAD；

（2）由（1）中的全等得：∠OAB=∠OBA，根据等角对等边可得结论．

【解答】证明：（1）∵AD⊥AB，BC⊥AB，

∴∠DAB=∠ABC=90°，

∵AD=BC，AB=BA，

∴△ABC≌△BAD（SAS）；

（2）∵△ABC≌△BAD，

∴∠OAB=∠OBA，

∴OA=OB．

【点评】本题考查了全等三角形的性质和判定，比较简单，属于基础题；熟练掌握全等的判定方法是解题的关键：①SSS，②SAS，③AAS，④ASA；还要知道全等判定中的隐含条件：公共边、公共角和对顶角等．

第72题

在正方形网格中，△ABC各顶点都在格点上，点A、C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：

（1）画出△ABC关于y轴对称的△A₁B₁C₁；

参考答案：见解析

解析：

【分析】（1）找出对称点A₁、B₁、C₁，连点成线即可得出结论；

（2）找出对称点A₂、B₂、C₂，连点成线即可得出结论；

（3）根据点C的坐标，结合对称点的特点即可找出点C₁、C₂的坐标，此题得解．

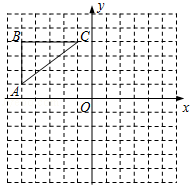
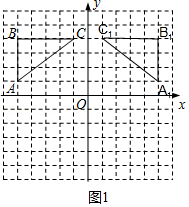
【解答】解：（1）画出△ABC关于y轴对称的△A₁B₁C₁，如图1所示．

（2）画出△ABC关于x轴对称的△A₂B₂C₂，如图2所示．

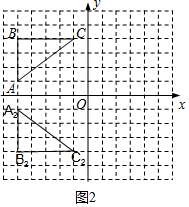
（3）∵点C的坐标为（﹣1，4），

∴点C₁的坐标是（1，4）；点C₂的坐标是（﹣1，﹣4）．

故答案为：（1，4）；（﹣1，﹣4）．

【点评】本题考查了作图中的轴对称变换，熟练掌握图形关于某直线对称图形的画法是解题的关键．

第73题

计算并观察下列各式：

（x﹣1）（x+1）=　　；

参考答案：见解析

解析：

【分析】（1）利用平方差公式，依此类推得到结果即可；

（2）利用发现的规律填写即可；

（3）利用得出的规律计算得到结果；

（4）原式变形后，利用得出的规律计算即可得到结果．

【解答】解：（1）（x﹣1）（x+1）=x²﹣1；

（x﹣1）（x²+x+1）=x³﹣1；

（x﹣1）（x³+x²+x+1）=x⁴﹣1；

（2）（x﹣1）（x⁵+x⁴+x³+x²+x+1）=x⁶﹣1；

（3）利用你发现的规律计算：

（x﹣1）（x⁶+x⁵+x⁴+x³+x²+x+1）=x⁷﹣1；

（4）1+4+4²+4³+…+4²⁰¹³=×（4﹣1）×（1+4+4²+4³+…+4²⁰¹³）=（4²⁰¹⁴﹣1）．

故答案为：（1）x²﹣1；x³﹣1；x⁴﹣1；（2）x⁵+x⁴+x³+x²+x+1；（3）x⁷﹣1；（4）（4²⁰¹⁴﹣1）．

【点评】此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．

第74题

某文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．

（1）求第一批购进书包的单价是多少元？

参考答案：见解析

解析：

【分析】（1）求的是单价，总价明显，一定是根据数量来列等量关系．本题的关键描述语是：“数量是第一批购进数量的3倍”；等量关系为：6300元购买的数量=2000元购买的数量×3．

（2）盈利=总售价﹣总进价．

【解答】解：（1）设第一批购进书包的单价是x元．

则：×3=．

解得：x=80．

经检验：x=80是原方程的根．

答：第一批购进书包的单价是80元．

（2）×（120﹣80）+×（120﹣84）=3700（元）．

答：商店共盈利3700元．

【点评】应用题中一般有三个量，求一个量，明显的有一个量，一定是根据另一量来列等量关系的．本题考查分式方程的应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．

第75题

若分式有意义，则x的取值应满足（　　）

A.x≠3

B.x≠4

C.x≠﹣4

D.x≠﹣3

参考答案：C

解析：

【考点】分式有意义的条件．

【分析】根据分式有意义的条件是分母不等于零列出不等式，解不等式即可．

【解答】解：由题意得，x+4≠0，

解得x≠﹣4．

故选：C．

第76题

若某三角形的两边长分别为3和4，则下列长度的线段能作为其第三边的是（　　）

A.1

B.5

C.7

D.9

参考答案：B

解析：

【考点】三角形三边关系．

【分析】此题首先根据三角形的三边关系，求得第三边的取值范围，再进一步找到符合条件的数值．

【解答】解：根据三角形的三边关系，得：第三边＞两边之差，即4﹣3=1，而＜两边之和，即4+3=7，

即1＜第三边＜7，

∴只有5符合条件，

故选：B．

第77题

下列运算中正确的是（　　）

A.（a²）³=a⁵

B.a²•a³=a⁵

C.a⁶÷a²=a³

D.a⁵+a⁵=2a¹⁰

参考答案：B

解析：

【考点】同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．

【分析】利用同底数幂的除法与乘方，幂的乘方与积的乘方及合并同类项的法则求解即可．

【解答】解：A、（a²）³=a⁶，故本选项错误；

B、a²•a³=a⁵，故本选项正确；

C、a⁶÷a²=a⁴，故本选项错误；

D、a⁵+a⁵=2a⁵，故本选项错误．

故选：B．

第78题

如图，△ABC沿AB向下翻折得到△ABD，若∠ABC=30°，∠ADB=100°，则∠BAC的度数是（　　）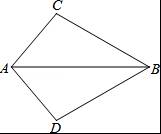

A.100°

B.30°

C.50°

D.80°

参考答案：C

解析：

【考点】翻折变换（折叠问题）．

【分析】由翻折的特点可知，∠ACB=∠ADB=100°，进一步利用三角形的内角和求得∠BAC的度数即可．

【解答】解：∵△ABC沿AB向下翻折得到△ABD，

∴∠ACB=∠ADB=100°，

∴∠BAC=180°﹣∠ACB﹣∠ABC

=180°﹣100°﹣30°

=50°．

故选：C．

第79题

如果分式的值为零，那么x等于（　　）

A.1

B.﹣1

C.0

D.±1

参考答案：B

解析：

【考点】分式的值为零的条件．

【分析】根据分式的值为0的条件及分式有意义的条件列出关于x的不等式组，求出x的值即可．

【解答】解：∵分式的值为零，

∴，

解得x=﹣1．

故选B．

第80题

如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（　　）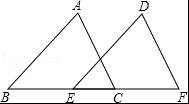

A.∠A=∠D

B.BC=EF

C.∠ACB=∠F

D.AC=DF

参考答案：D

解析：

【考点】全等三角形的判定．

【分析】根据全等三角形的判定，利用ASA、SAS、AAS即可得答案．

【解答】解：∵∠B=∠DEF，AB=DE，

∴添加∠A=∠D，利用ASA可得△ABC≌△DEF；

∴添加BC=EF，利用SAS可得△ABC≌△DEF；

∴添加∠ACB=∠F，利用AAS可得△ABC≌△DEF；

故选D．