第41题

如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB=8cm，则△BED的周长是　　．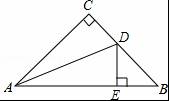

参考答案：8cm

解析：

【考点】角平分线的性质；等腰直角三角形．

【分析】根据角平分线上的点到角的两边的距离相等可得CD=DE，再根据“HL”证明△ACD和△AED全等，根据全等三角形对应边相等可得AC=AE，然后求出△BED的周长=AB，即可得解．

【解答】解：∵∠C=90°，AD平分∠CAB，DE⊥AB，

∴CD=DE，

在△ACD和△AED中，，

∴△ACD≌△AED（HL），

∴AC=AE，

∴△BED的周长=DE+BD+BE，

=BD+CD+BE，

=BC+BE，

=AC+BE，

=AE+BE，

=AB，

∵AB=8cm，

∴△BED的周长是8cm．

故答案为：8cm．

【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，熟记性质并求出△BED的周长=AB是解题的关键．

第42题

解方程：﹣=0．

参考答案：见解析

解析：

【考点】解分式方程．

【专题】计算题．

【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

【解答】解：去分母得：4x﹣8﹣3x=0，

解得：x=8，

经检验x=8是分式方程的解．

【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

第43题

一个多边形内角和是一个四边形内角和的4倍，请求出这个多边形的边数．

参考答案：见解析

解析：

【考点】多边形内角与外角．

【分析】设这个多边形的边数为n，根据n边形的内角和的计算公式（n﹣2）•180°列出方程，解方程即可．

【解答】解：设这个多边形的边数为n，

由题意得，（n﹣2）×180°=360°×4，

解得：n=10．

答：这个多边形的边数为10．

【点评】本题考查的是多边形的内角和和外角和的计算，掌握n边形的内角和的计算公式：（n﹣2）•180°是解题的关键．

第44题

如图，在平面直角坐标系xOy中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

（1）求出△ABC的面积．

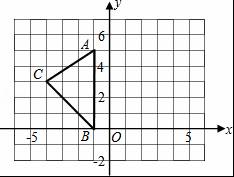
参考答案：见解析

解析：

【考点】作图-轴对称变换．

【专题】综合题．

【分析】（1）根据网格可以看出三角形的底AB是5，高是C到AB的距离，是3，利用面积公式计算．

（2）从三角形的各顶点向y轴引垂线并延长相同长度，找对应点．顺次连接即可．

（3）从图中读出新三角形三点的坐标．

【解答】解：（1）S_△ABC=×5×3=（或7.5）（平方单位）．

（2）如图．

（3）A₁（1，5），B₁（1，0），C₁（4，3）．

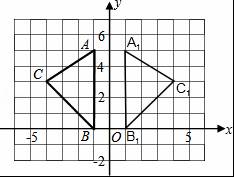
【点评】本题综合考查了三角形的面积，网格，轴对称图形，及直角坐标系，学生对所学的知识要会灵活运用．

第45题

先化简，再求值：÷（1+），其中x=﹣1．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】分式的化简，要熟悉混合运算的顺序，分子、分母能因式分解的先因式分解；除法要统一为乘法运算，注意化简后，将，代入化简后的式子求出即可．

【解答】解：

=÷（+）

=÷

=×

=，

把，代入原式====．

【点评】此题主要考查了分式混合运算，要注意分子、分母能因式分解的先因式分解；除法要统一为乘法运算是解题关键

第46题

如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．

（1）求证：BE=CE；

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等腰三角形的性质．

【专题】证明题．

【分析】（1）根据等腰三角形三线合一的性质可得∠BAE=∠EAC，然后利用“边角边”证明△ABE和△ACE全等，再根据全等三角形对应边相等证明即可；

（2）先判定△ABF为等腰直角三角形，再根据等腰直角三角形的两直角边相等可得AF=BF，再根据同角的余角相等求出∠EAF=∠CBF，然后利用“角边角”证明△AEF和△BCF全等即可．

【解答】证明：（1）∵AB=AC，D是BC的中点，

∴∠BAE=∠EAC，

在△ABE和△ACE中，，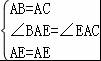

∴△ABE≌△ACE（SAS），

∴BE=CE；

（2）∵∠BAC=45°，BF⊥AF，

∴△ABF为等腰直角三角形，

∴AF=BF，

∵AB=AC，点D是BC的中点，

∴AD⊥BC，

∴∠EAF+∠C=90°，

∵BF⊥AC，

∴∠CBF+∠C=90°，

∴∠EAF=∠CBF，

在△AEF和△BCF中，，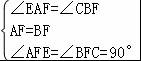

∴△AEF≌△BCF（ASA）．

【点评】本题考查了全等三角形的判定与性质，等腰三角形三线合一的性质，等腰直角三角形的判定与性质，同角的余角相等的性质，是基础题，熟记三角形全等的判定方法与各性质是解题的关键．

第47题

一项工程，甲，乙两公司合作，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．

（1）甲，乙两公司单独完成此项工程，各需多少天？

参考答案：见解析

解析：

【考点】分式方程的应用；一元一次方程的应用．

【分析】（1）设甲公司单独完成此项工程需x天，则乙工程公司单独完成需1.5x天，根据合作12天完成列出方程求解即可．

（2）分别求得两个公司施工所需费用后比较即可得到结论．

【解答】解：（1）设甲公司单独完成此项工程需x天，则乙公司单独完成此项工程需1.5x天．

根据题意，得+=，

解得x=20，

经检验知x=20是方程的解且符合题意．

1.5x=30

故甲公司单独完成此项工程，需20天，乙公司单独完成此项工程，需30天；

（2）设甲公司每天的施工费为y元，则乙公司每天的施工费为（y﹣1500）元，

根据题意得12（y+y﹣1500）=102000，解得y=5000，

甲公司单独完成此项工程所需的施工费：20×5000=100000（元）；

乙公司单独完成此项工程所需的施工费：30×（5000﹣1500）=105000（元）；

故甲公司的施工费较少．

【点评】本题考查了分式方程的应用，解题的关键是从实际问题中整理出等量关系并利用等量关系求解．

第48题

下列各组数不可能是一个三角形的边长的是（　　）

A.5，12，13

B.5，7，12

C.5，7，7

D.4，6，9

参考答案：B

解析：

【分析】看哪个选项中两条较小的边的和小于最大的边即可．

【解答】解：A、5+12＞13，能构成三角形；

B、5+7=12，不能构成三角形；

C、5+7＞7，能构成三角形；

D、4+6＞9，能构成三角形．

故选B．

【点评】本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，只要满足两短边的和大于最长的边，就可以构成三角形．

第49题

一个正多边形的内角和是1080°，则它是（　　）边形．

A.六

B.七

C.八

D.九

参考答案：C

解析：

【分析】根据多边形内角和公式结合该多边形内角和为1080°，即可算出该多边形的边数，由此即可得出结论．

【解答】解：（1080°+360°）÷180°=8，

∴该正多边形为正八边形．

故选C．

【点评】本题考查了多边形内角与外角，解题的关键是牢牢掌握多边形内角和公式．

第50题

如图，已知△ABC≌△DEF，则∠C的对应角为（　　）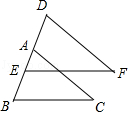

A.∠F

B.∠AGE

C.∠AEF

D.∠D

参考答案：A

解析：

【分析】根据全等三角形的对应角相等解答．

【解答】解：∵△ABC≌△DEF，

∴∠C的对应角为∠F，

故选：A．

【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．

第51题

下列四副图案中，不是轴对称图形的是（　　）

A.

B.

C.

D.

参考答案：A

解析：

【分析】直接利用轴对称图形的概念求解即可求得答案．注意掌握排除法在选择题中的应用．

【解答】解：轴对称图形的是B，C，D；不是轴对称图形的是A．

故选A．

【点评】此题考查了轴对称图形的定义．注意准确理解轴对称图形的定义是解此题的关键．

第52题

若等腰三角形的顶角为40°，则它的底角度数为（　　）

A.40°

B.50°

C.60°

D.70°

参考答案：D

解析：

【分析】根据等腰三角形的性质和三角形内角和定理可直接求出其底角的度数．

【解答】解：因为等腰三角形的两个底角相等，

又因为顶角是40°，

所以其底角为=70°．

故选：D．

【点评】此题考查学生对等腰三角形的性质的理解和掌握，解答此题的关键是知道等腰三角形的两个底角相等．

第53题

下列运算中，正确的是（　　）

A.a⁸÷a²=a⁴

B.（﹣m）²•（﹣m³）=﹣m⁵

C.x³+x³=x⁶

D.（a³）³=a⁶

参考答案：B

解析：

【分析】计算出各个选项中式子的正确结果，即可得到哪个选项是正确的．

【解答】解：∵a⁸÷a²=a⁶，故选项A错误；

∵（﹣m）²•（﹣m³）=﹣m⁵，故选项B正确；

∵x³+x³=2x³，故选项C错误；

∵（a³）³=a⁹，故选项D错误；

故选B．

【点评】本题考查整式的混合运算，解题的关键是明确整式的混合运算的计算方法．

第54题

若a﹣b=3，则a²﹣2ab+b²﹣6的值是（　　）

A.12

B.6

C.3

D.0

参考答案：C

解析：

【分析】由完全平方公式，可得a²﹣2ab+b²﹣6=（a﹣b）²﹣6，继而求得答案．

【解答】解：∵a﹣b=3，

∴a²﹣2ab+b²﹣6=（a﹣b）²﹣6=3²﹣6=3．

故选C．

【点评】此题考查了完全平方公式的应用．注意利用完全平方公式将原式变形为（a﹣b）²﹣6是解此题的关键．

第55题

下列各式从左边到右边的变形是因式分解的为（　　）

A.（a+1）（a﹣1）=a²﹣1

B.﹣18x⁴y³=﹣6x²y²•3x²y

C.x²+2x+1=x（x+2x）+1

D.a²﹣6a+9=（a﹣3）²

参考答案：D

解析：

【分析】分解因式就是把一个多项式化为几个整式的积的形式．因此，要确定从左到右的变形中是否为分解因式，只需根据定义来确定．

【解答】解：A、是多项式乘法，不是因式分解，错误；

B、左边是单项式，不是因式分解，错误；

C、右边不是积的形式，错误；

D、是因式分解，正确．

故选D．

【点评】本题的关键是理解因式分解的定义：把一个多项式化为几个最简整式的积的形式，这种变形叫做把这个多项式因式分解，然后进行正确的因式分解．

第56题

使代数式有意义的x的取值范围是（　　）

A.x＞3

B.x=3

C.x＜3

D.x≠3

参考答案：D

解析：

【分析】根据分式有意义的条件：分母≠0，据此即可解不等式求解．

【解答】解：根据题意得：x﹣3≠0，

解得：x≠3．

故选D．

【点评】本题考查了分式有意义的条件，分母不等于0，理解有意义的条件是关键．

第57题

一艘轮船在静水中的最大航速是30km/h，它以最大航速沿江顺流航行90km所用时间，与它以最大航速逆流航行60km所用时间相等．如果设江水的流速为x km/h，所列方程正确的是（　　）

A.

B.

C.

D.

参考答案：C

解析：

【分析】设江水的流速为x km/h，则逆流的速度为（30﹣x）km/h，顺流的速度为（30+x）km/h，根据顺流航行90km所用时间，与逆流航行60km所用时间相等，列方程即可．

【解答】解：设江水的流速为x km/h，则逆流的速度为（30﹣x）km/h，顺流的速度为（30+x）km/h，

由题意得，=．

故选C．

【点评】本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．

第58题

盖房子时，在窗框未安装之前，木工师傅常常先在窗框上斜钉上一根木条，这是利用了三角形具有　　的原理．

参考答案：稳定性

解析：

【分析】在窗框上斜钉一根木条，构成三角形，故可用三角形的稳定性解释．

【解答】解：盖房子时，在窗框未安装好之前，木工师傅常常先在窗框上斜钉一根木条，这样就构成了三角形，故这样做的数学道理是三角形的稳定性．

故答案为：稳定性．

【点评】本题考查三角形稳定性的实际应用，三角形的稳定性在实际生活中有着广泛的应用，要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．

第59题

一个多边形的内角和是外角和的2倍，则这个多边形的边数为　　．

参考答案：6

解析：

【分析】利用多边形的外角和以及多边形的内角和定理即可解决问题．

【解答】解：∵多边形的外角和是360度，多边形的内角和是外角和的2倍，

则内角和是720度，

720÷180+2=6，

∴这个多边形是六边形．

故答案为：6．

【点评】本题主要考查了多边形的内角和定理与外角和定理，熟练掌握定理是解题的关键．

第60题

8²⁰¹⁶×0.125²⁰¹⁵=　　．

参考答案：8

解析：

【分析】直接利用积的乘方运算法则将原式变形求出答案．

【解答】解：原式=（8×0.125）²⁰¹⁵×8

=8．

故答案为：8．

【点评】此题主要考查了积的乘方运算和有理数的乘法运算，正确应用积的乘方运算法则是解题关键．