第121题

计算

（1）（﹣3ab^﹣1）²•（a^﹣2b²）^﹣3

参考答案：见解析

解析：

【考点】分式的混合运算；负整数指数幂．

【分析】（1）原式利用幂的乘方与积的乘方运算法则计算即可得到结果；

（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．

【解答】解：（1）（﹣3ab^﹣1）²•（a^﹣2b²）^﹣3

=9a²b^﹣2•a⁶b^﹣6

=9a⁸b^﹣8

=；

（2）÷（a﹣）

=÷

=•

=．

第122题

阅读下面的问题，然后回答，

分解因式：x²+2x﹣3，

参考答案：见解析

解析：

【考点】因式分解-十字相乘法等；因式分解-分组分解法．

【分析】根据题意给出的方法即可求出答案．

【解答】解：（1）x²﹣4x+3

=x²﹣4x+4﹣4+3

=（x﹣2）²﹣1

=（x﹣2+1）（x﹣2﹣1）

=（x﹣1）（x﹣3）

（2）4x²+12x﹣7

=4x²+12x+9﹣9﹣7

=（2x+3）²﹣16

=（2x+3+4）（2x+3﹣4）

=（2x+7）（2x﹣1）

第123题

（1）如图1：在△ABC中，AB=AC，AD⊥BC，DE⊥AB于点E，DF⊥AC于点F．证明：DE=DF．

（2）如图2，在△ABC中，AB=AC，AD⊥BC，DE和DF分别平分∠ADB和∠ADC，求证：DE=DF．

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；角平分线的性质．

【分析】（1）由等腰三角形的性质和角平分线的性质定理直接证明即可；

（2）利用等腰三角形的性质和全等三角形的判定定理ASA证得△AED≌△AFD，则由该全等三角形的对应边相等得到DE=DF．

【解答】解：

（1）证明：∵AB=AC，AD⊥BC，

∴∠BAD=∠CAD，

∵DE⊥AB，DF⊥AC

∴DE=DF；

（2）证明：∵AB=AC，AD⊥BC

∴∠BAD=∠CAD，

∵DE平分∠ADB，DF平分和∠ADC，

∴∠ADE=∠ADF=45°，

在△AED和△AFD中，

，

∴△AED≌△AFD（ASA），

∴DE=DF．

第124题

元旦晚会上，王老师要为她的学生及班级的六位科任老师送上贺年卡，网上购买贺年卡的优惠条件是：购买50或50张以上享受团购价．王老师发现：零售价与团购价的比是5：4，王老师计算了一下，按计划购买贺年卡只能享受零售价，如果比原计划多购买6张贺年卡就能享受团购价，这样她正好花了100元，而且比原计划还节约10元钱；

（1）贺年卡的零售价是多少？

参考答案：见解析

解析：

【考点】分式方程的应用．

【分析】（1）首先设零售价为5x元，团购价为4x元，由题意可得等量关系：零售价用110元所购买的数量+6=团购价用100元所购买的数量，根据等量关系列出方程，计算出x的值；

（2）根据（1）中求得的贺年卡的零售价求学生数．

【解答】解：（1）设零售价为5x元，团购价为4x元，则

解得，，

经检验：x=是原分式方程的解，

5x=2.5

答：零售价为2.5元；

（2）学生数为=38（人）

答：王老师的班级里有38名学生．

第125题

（1）如图①，你知道∠BOC=∠B+∠C+∠A的奥秘吗？请你用学过的知识予以证明；

（2）如图②﹣1，则∠A+∠B+∠C+∠D+∠E=　　°；

参考答案：见解析

解析：

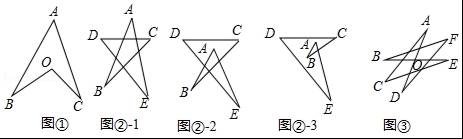
【考点】多边形内角与外角；三角形内角和定理；三角形的外角性质．

【分析】（1）首先延长BO交AC于点D，可得BOC=∠BDC+∠C，然后根据∠BDC=∠A+∠B，判断出∠BOC=∠B+∠C+∠A即可．

（2）a、首先根据外角的性质，可得∠1=∠A+∠B，∠2=∠C+∠D，然后根据∠1+∠2+∠E=180°，可得x=∠A+∠B+∠C+∠D+∠E=180，据此解答即可．

b、首先根据外角的性质，可得∠1=∠A+∠B，∠2=∠C+∠D，然后根据∠1+∠2+∠E=180°，可得x=∠A+∠B+∠C+∠D+∠E=180，据此解答即可．

c、首先延长EA交CD于点F，EA和BC交于点G，然后根据外角的性质，可得∠GFC=∠D+∠E，∠FGC=∠A+∠B，再根据∠GFC+∠FGC+∠C=180°，可得x=∠A+∠B+∠C+∠D+∠E=180°，据此解答即可．

（3）根据∠BOD=70°，可得∠A+∠C+∠E=70°，∠B+∠D+∠F=70°，据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可．

【解答】解：（1）如图①，延长BO交AC于点D，

∠BOC=∠BDC+∠C，

又∵∠BDC=∠A+∠B，

∴∠BOC=∠B+∠C+∠A．

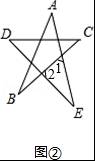
（2）如图②，

，

根据外角的性质，可得

∠1=∠A+∠B，∠2=∠C+∠D，

∵∠1+∠2+∠E=180°，

∴x=∠A+∠B+∠C+∠D+∠E=180°．

如图③，

，

根据外角的性质，可得

∠1=∠A+∠B，∠2=∠C+∠D，

∵∠1+∠2+∠E=180°，

∴x=∠A+∠B+∠C+∠D+∠E=180°．

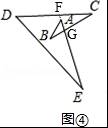
如图④，延长EA交CD于点F，EA和BC交于点G，

，

根据外角的性质，可得

∠GFC=∠D+∠E，∠FGC=∠A+∠B，

∵∠GFC+∠FGC+∠C=180°，

∴x=∠A+∠B+∠C+∠D+∠E=180°．

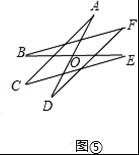
（3）如图⑤，

，

∵∠BOD=70°，

∴∠A+∠C+∠E=70°，

∴∠B+∠D+∠F=70°，

∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°．

故答案为：180、180、180、140．

第126题

计算下列各式：

（x﹣1）（x+1）=　　；

参考答案：见解析

解析：

【考点】整式的混合运算；规律型：数字的变化类．

【分析】利用多项式乘以多项式法则计算各式即可；

（1）根据上述规律写出结果即可；

（2）归纳总结得到一般性规律，写出即可；

（3）利用得出的规律计算即可得到结果．

【解答】解：（x﹣1）（x+1）=x²﹣1；

（x﹣1）（x²+x+1）=x³﹣1；

（x﹣1）（x³+x²+x+1）=x⁴﹣1，

故答案为：x²﹣1；x³﹣1；x⁴﹣1；

（1）（x﹣1）（x⁶+x⁵+x⁴+x³+x²+x+1）=x⁷﹣1；

（2）（x﹣1）（x^n﹣1+x^n﹣2+x^n﹣3+…+x+1）=xⁿ﹣1；

故答案为：（1）x⁷﹣1；（2）xⁿ﹣1；

（3）1+2+2²+2³+2⁴+…+2³⁵

=（2﹣1）

=2³⁶﹣1．

第127题

（1）问题背景：

如图①：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E、F分别是BC、CD上的点．且∠EAF=60°．探究图中线段BE、EF、FD之间的数量关系．小明同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　　；

参考答案：见解析

解析：

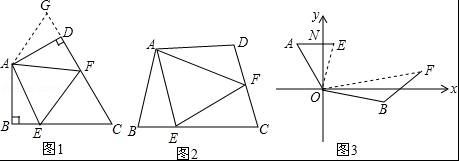
【考点】四边形综合题．

【分析】（1）根据全等三角形的判定与性质，可得AG与BE的关系，∠BAE与∠DAG的关系，根据全等三角形的判定与性质，可得EF与GF的关系，根据等量代换，可得答案；

（2）根据补角的性质，可得∠B=∠ADG，根据全等三角形的判定与性质，可得AG与BE的关系，∠BAE与∠DAG的关系，根据全等三角形的判定与性质，可得EF与GF的关系，根据等量代换，可得答案；

（3）根据角的和差，可得∠OEF与∠AOB的关系，∠A与∠B的关系，根据（2）的探索，可得EF与AE、BF的关系，可得答案．

【解答】解：（1）在△ABE和△ADG中，

，

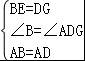∴△ABE≌△ADG（SAS），

∴AE=AG，∠BAE=∠DAG．

∵∠EAF=∠BAD，

∴∠BAE+∠DAF=∠EAF=∠BAD．

∵∠GAF=∠DAG+∠DAF，

∴∠GAF=∠BAE+∠DAF．

∴∠EAF=∠GAF，

在△AEF和△GAF中，

，

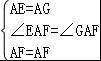∴△AEF≌△GAF（SAS），

∴EF=FG，

∵FG=DG+DF=BE+DF，

故答案为：EF=BE+DF；

（2）EF=BE+DF仍然成立．

证明：如图1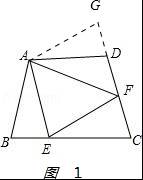，延长FD到G，使DG=BE，连接AG，

∵∠B+∠ADC=180°，∠ADC+∠ADG=180°，

∴∠B=∠ADG，

在△ABE和△ADG中，

，

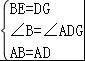∴△ABE≌△ADG（SAS），

∴AE=AG，∠BAE=∠DAG．

∵∠EAF=∠BAD，

∴∠BAE+∠DAF=∠EAF=∠BAD．

∵∠GAF=∠DAG+∠DAF，

∴∠GAF=∠BAE+∠DAF．

∴∠EAF=∠GAF，

在△AEF和△GAF中，

，

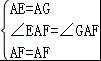∴△AEF≌△GAF（SAS），

∴EF=FG，

∵FG=DG+DF=BE+DF，

∴EF=BE+DF；

（3）如图2，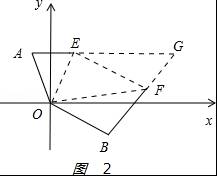

连接EF，延长AE、BF相交于点C，

∵∠AOB=∠AON+∠NCH+∠BOH=30+90+20=140°，

∠EOF=70°，

∴∠EOF=∠AOB，

又∵OA=OB，∠OAC+∠OBC=（90°﹣30°）+（70°+50°）=180°，

∴符合探索延伸中的条件，

∴结论EF=AE+BF成立，

即EF=2×（60+80）=280海里．

答：此时两舰艇之间的距离是280海里．

第128题

下面四个图案中，是轴对称图形的是（　　）

A.

B.

C.

D.

参考答案：D

解析：

【考点】轴对称图形．

【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解．

【解答】解：A、不是轴对称图形，故本选项错误；

B、不是轴对称图形，故本选项错误；

C、不是轴对称图形，故本选项错误；

D、是轴对称图形，故本选项正确．

故选D．

第129题

若分式的值为0，则x的值为（　　）

A.﹣1

B.0

C.2

D.﹣1或2

参考答案：A

解析：

【考点】分式的值为零的条件．

【分析】根据分式的分子为0；分母不为0，分式的值为零，可得答案．

【解答】解：由分式的值为0，得

，解得x=﹣1，

故选：A．

第130题

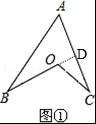
如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（　　）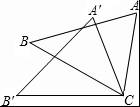

A.20°

B.30°

C.35°

D.40°

参考答案：B

解析：

【考点】全等三角形的性质．

【分析】本题根据全等三角形的性质并找清全等三角形的对应角即可．

【解答】解：∵△ACB≌△A′CB′，

∴∠ACB=∠A′CB′，

即∠ACA′+∠A′CB=∠B′CB+∠A′CB，

∴∠ACA′=∠B′CB，

又∠B′CB=30°

∴∠ACA′=30°．

故选：B．

第131题

下列各式由左边到右边的变形中，属于分解因式的是（　　）

A.a（x+y）=ax+ay

B.x²﹣4x+4=x（x﹣4+）

C.10x²﹣5x=5x（2x﹣1）

D.x²﹣16+3x=（x+4）（x﹣4）+3x

参考答案：C

解析：

【考点】因式分解的意义．

【分析】利用因式分解的意义判断即可．

【解答】解：下列各式由左边到右边的变形中，属于分解因式的是10x²﹣5x=5x（2x﹣1），

故选C

第132题

如果一个多边形的每个内角都相等，且内角和为1800度，那么这个多边形的一个外角是（　　）

A.30°

B.36°

C.60°

D.72°

参考答案：A

解析：

【考点】多边形内角与外角．

【分析】设这个多边形是n边形，它的内角和可以表示成（n﹣2）•180°，就得到关于n的方程，求出边数n．然后根据多边形的外角和是360°，多边形的每个内角都相等即每个外角也相等，这样就能求出多边形的一个外角．

【解答】解：设这个多边形是n边形，

根据题意得：（n﹣2）•180°=1800，

解得n=12；

那么这个多边形的一个外角是360÷12=30度，

即这个多边形的一个外角是30度．

故本题选A．

第133题

化简的结果是（　　）

A.m

B.

C.﹣m

D.﹣

参考答案：C

解析：

【考点】分式的乘除法．

【分析】原式利用除法法则变形，约分即可得到结果．

【解答】解：原式=﹣•=﹣m．

故选C

第134题

用一条长为16cm的细绳围成一个等腰三角形，若其中有一边的长为4cm，则该等腰三角形的腰长为（　　）

A.4cm

B.6cm

C.4cm或6cm

D.4cm或8cm

参考答案：B

解析：

【考点】等腰三角形的性质；三角形三边关系．

【分析】分已知边4cm是腰长和底边两种情况讨论求解．

【解答】解：4cm是腰长时，底边为16﹣4×2=8，

∵4+4=8，

∴4cm、4cm、8cm不能组成三角形；

4cm是底边时，腰长为（16﹣4）=6cm，

4cm、6cm、6cm能够组成三角形；

综上所述，它的腰长为6cm．

故选：B．

第135题

若3^x=4，3^y=6，则3^x﹣2y的值是（　　）

A.

B.9

C.

D.3

参考答案：A

解析：

【考点】同底数幂的除法；幂的乘方与积的乘方．

【分析】利用同底数幂的除法运算法则得出3^x﹣2y=3^x÷（3^y）²，进而代入已知求出即可．

【解答】解：3^x﹣2y=3^x÷（3^y）²=4÷6²=．

故选：A．

第136题

如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE=2，当EF+CF取得最小值时，则∠ECF的度数为（　　）

A.15°

B.22.5°

C.30°

D.45°

参考答案：C

解析：

【考点】轴对称-最短路线问题；等边三角形的性质．

【分析】过E作EM∥BC，交AD于N，连接CM交AD于F，连接EF，推出M为AB中点，求出E和M关于AD对称，根据等边三角形性质求出∠ACM，即可求出答案．

【解答】解：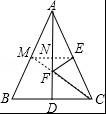

过E作EM∥BC，交AD于N，

∵AC=4，AE=2，

∴EC=2=AE，

∴AM=BM=2，

∴AM=AE，

∵AD是BC边上的中线，△ABC是等边三角形，

∴AD⊥BC，

∵EM∥BC，

∴AD⊥EM，

∵AM=AE，

∴E和M关于AD对称，

连接CM交AD于F，连接EF，

则此时EF+CF的值最小，

∵△ABC是等边三角形，

∴∠ACB=60°，AC=BC，

∵AM=BM，

∴∠ECF=∠ACB=30°，

故选C．

第137题

一粒芝麻约有0.000002千克，0.000002用科学记数法表示为　　千克．

参考答案：2×10^﹣6

解析：

【考点】科学记数法—表示较小的数．

【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10^﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【解答】解：0.000002用科学记数法表示为 2×10^﹣6千克，

故答案为：2×10^﹣6．

第138题

如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为　　．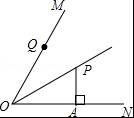

参考答案：3

解析：

【考点】角平分线的性质；垂线段最短．

【分析】根据垂线段最短可知PQ⊥OM时，PQ的值最小，再根据角平分线上的点到角的两边的距离相等可得PQ=PA．

【解答】解：根据垂线段最短，PQ⊥OM时，PQ的值最小，

∵OP平分∠MON，PA⊥ON，

∴PQ=PA=3．

故答案为：3．

第139题

如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为　　．

参考答案：（6a+15）cm²

解析：

【考点】图形的剪拼．

【分析】利用大正方形的面积减去小正方形的面积即可，注意完全平方公式的计算．

【解答】解：矩形的面积为：

（a+4）²﹣（a+1）²

=（a²+8a+16）﹣（a²+2a+1）

=a²+8a+16﹣a²﹣2a﹣1

=6a+15．

故答案为：（6a+15）cm²，

第140题

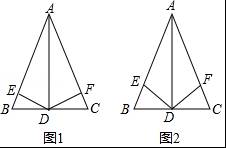
如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，则∠DAE的度数为　　．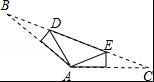

参考答案：100°

解析：

【考点】翻折变换（折叠问题）．

【分析】如图，由三角形内角和定理求出∠B+∠C=40°；证明∠ADE+∠AED=2（α+β）=80°，即可解决问题．

【解答】解：如图，∵∠BAC=140°，

∴∠B+∠C=180°﹣140°=40°；

由题意得：∠B=∠DAB（设为α），∠C=∠EAC（设为β），

∴∠ADE=2α，∠AED=2β，

∴∠DAE=180°﹣2（α+β）=180°﹣80°=100°，

故答案为100°．