第101题

下列图形对称轴最多的是（　　）

A.正方形

B.等边三角形

C.等腰三角形

D.线段

参考答案：A

解析：

【考点】轴对称图形．

【分析】根据轴对称图形的对称轴的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做轴对称图形的对称轴．

【解答】解：A、有4条对称轴，即两条对角线所在的直线和两组对边的垂直平分线；

B、有3条对称轴，即各边的垂直平分线；

C、有1条对称轴，即底边的垂直平分线；

D、有2条对称轴．

故选：A．

第102题

如果分式的值是零，则x的取值是（　　）

A.x=1

B.x=﹣1

C.x=±1

D.x=0

参考答案：A

解析：

【考点】分式的值为零的条件．

【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0．

【解答】解：由题意可得x+1≠0且x²﹣1=0，

解得x=1．

故选A．

第103题

已知点P（1，a）与Q（b，2）关于x轴成轴对称，则a﹣b的值为（　　）

A.﹣1

B.1

C.﹣3

D.3

参考答案：C

解析：

【考点】关于x轴、y轴对称的点的坐标．

【分析】关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得a、b的值．

【解答】解：∵点P（1，a）与Q（b，2）关于x轴成轴对称，

∴b=1，a=﹣2，

∴a﹣b=﹣3，

故选：C．

第104题

1纳米等于0.000000001米，则35纳米用科学记数法表示为（　　）

A.35×10^﹣9米

B.3.5×10^﹣9米

C.3.5×10^﹣10米

D.3.5×10^﹣8米

参考答案：D

解析：

【考点】科学记数法—表示较小的数．

【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10^﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【解答】解：35×0.000000001=3.5×10^﹣8；

故选：D．

第105题

如图，△ABC≌△ADE，若∠B=80°，∠C=30°，∠DAC=25°，则∠EAC的度数为（　　）

A.45°

B.40°

C.35°

D.25°

参考答案：A

解析：

【考点】全等三角形的性质．

【分析】根据全等三角形的性质求出∠D和∠E，根据三角形内角和定理计算即可．

【解答】解：∵△ABC≌△ADE，

∴∠D=∠B=80°，∠E=∠C=30°，

∴∠DAE=180°﹣∠D﹣∠E=70°，

∴∠EAC=∠EAD﹣∠DAC=45°，

故选：A．

第106题

根据分式的基本性质，分式可变形为（　　）

A.

B.

C.

D.

参考答案：C

解析：

【考点】分式的基本性质．

【分析】分式的恒等变形是依据分式的基本性质，分式的分子分母同时乘以或除以同一个非0的数或式子，分式的值不变．

【解答】解：依题意得： =，故选C．

第107题

如图，AE，AD分别是△ABC的高和角平分线，且∠B=36°，∠C=76°，则∠DAE的度数为（　　）

A.40°

B.20°

C.18°

D.38°

参考答案：B

解析：

【考点】三角形的外角性质；三角形内角和定理．

【分析】△ABC中已知∠B=36°，∠C=76°，就可知道∠BAC的度数，则∠BAE就可求出；∠DAE是直角三角形△ADE的一个内角，则∠DAE=90°﹣∠ADE．

【解答】解：∵△ABC中已知∠B=36°，∠C=76，

∴∠BAC=68°．

∴∠BAD=∠DAC=34，

∴∠ADC=∠B+∠BAD=70°，

∴∠DAE=20°．

故填B．

第108题

计算：85²﹣15²=（　　）

A.70

B.700

C.4900

D.7000

参考答案：D

解析：

【考点】因式分解-运用公式法．

【分析】直接利用平方差进行分解，再计算即可．

【解答】解：原式=（85+15）（85﹣15）

=100×70

=7000．

故选：D．

第109题

已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为（　　）

A.2

B.3

C.5

D.13

参考答案：B

解析：

【考点】三角形三边关系．

【分析】根据三角形的三边关系：三角形两边之和大于第三边，两边差小于第三边；解答即可；

【解答】解：由题意可得，，

解得，11＜x＜15，

所以，x为12、13、14；

故选B．

第110题

若x²+mxy+4y²是完全平方式，则常数m的值为（　　）

A.4

B.﹣4

C.±4

D.以上结果都不对

参考答案：C

解析：

【考点】完全平方式．

【分析】完全平方公式：（a±b）²=a²±2ab+b²，这里首末两项是x和2y这两个数的平方，那么中间一项为加上或减去x和2y积的2倍，故m=±4．

【解答】解：∵（x±2y）²=x²±4xy+4y²，

∴在x²+mxy+4y²中，±4xy=mxy，

∴m=±4．

故选：C．

第111题

如图，给出下列四组条件：

①AB=DE，BC=EF，AC=DF；

A.1组

B.2组

C.3组

D.4组

参考答案：C

解析：

【考点】全等三角形的判定．

【分析】要使△ABC≌△DEF的条件必须满足SSS、SAS、ASA、AAS，可据此进行判断．

【解答】解：第①组满足SSS，能证明△ABC≌△DEF．

第②组满足SAS，能证明△ABC≌△DEF．

第③组满足ASA，能证明△ABC≌△DEF．

第④组只是SSA，不能证明△ABC≌△DEF．

所以有3组能证明△ABC≌△DEF．

故符合条件的有3组．

故选：C．

第112题

若a＞0且a^x=2，a^y=3，则a^x﹣y的值为（　　）

A.6

B.5

C.﹣1

D.

参考答案：D

解析：

【考点】同底数幂的除法．

【分析】根据同底数幂的除法公式即可求出答案．

【解答】解：由题意可知：

原式=a^x÷a^y=2÷3=

故选（D）

第113题

一个多边形截取一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为（　　）

A.5

B.5或6

C.5或7

D.5或6或7

参考答案：D

解析：

【考点】多边形内角与外角．

【分析】首先求得内角和为720°的多边形的边数，即可确定原多边形的边数．

【解答】解：设内角和为720°的多边形的边数是n，则（n﹣2）•180=720，

解得：n=6．

则原多边形的边数为5或6或7．

故选：D．

第114题

计算++的结果是（　　）

A.

B.

C.

D.

参考答案：A

解析：

【考点】分式的加减法．

【分析】原式通分并利用同分母分式的加减法则计算即可得到结果．

【解答】解：原式=

=

=，

故选A

第115题

如图，折叠直角三角形纸片的直角，使点C落在AB上的点E处，已知BC=24，∠B=30°，则DE的长是（　　）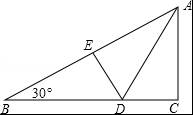

A.12

B.10

C.8

D.6

参考答案：C

解析：

【考点】翻折变换（折叠问题）．

【分析】由轴对称的性质可以得出DE=DC，∠AED=∠C=90°，就可以得出∠BED=90°，根据直角三角形的性质就可以求出BD=2DE，然后建立方程求出其解即可．

【解答】解：∵△ADE与△ADC关于AD对称，

∴△ADE≌△ADC，

∴DE=DC，∠AED=∠C=90°，

∴∠BED=90°．

∵∠B=30°，

∴BD=2DE．

∵BC=BD+CD=24，

∴24=2DE+DE，

∴DE=8．

故选：C．

第116题

如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点，若∠MON=35°，则∠GOH=（　　）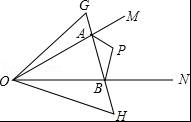

A.60°

B.70°

C.80°

D.90°

参考答案：B

解析：

【考点】轴对称的性质．

【分析】连接OP，根据轴对称的性质可得∠GOM=∠MOP，∠PON=∠NOH，然后求出∠GOH=2∠MON，代入数据计算即可得解．

【解答】解：如图，连接OP，

∵P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，

∴∠GOM=∠MOP，∠PON=∠NOH，

∴∠GOH=∠GOM+∠MOP+∠PON+∠NOH=2∠MON，

∵∠MON=35°，

∴∠GOH=2×35°=70°．

故选B．

第117题

若a^﹣1=（﹣1）⁰，则a=　　．

参考答案：1

解析：

【考点】负整数指数幂；零指数幂．

【分析】根据非零的零次幂等于1，负整数指数幂与正整数指数幂互为倒数，可得答案．

【解答】解：a^﹣1=（﹣1）⁰，得

a^﹣1==1，

解得a=1，

故答案为：1．

第118题

当x=2017时，分式的值为　　．

参考答案：2020

解析：

【考点】分式的值．

【分析】先把分式化简，再代入解答即可．

【解答】解：因为分式=，

把x=2017代入x+3=2020，

故答案为：2020．

第119题

平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2=　　．

参考答案：24°

解析：

【考点】多边形内角与外角．

【分析】首先根据多边形内角和定理，分别求出正三角形、正方形、正五边形、正六边形的每个内角的度数是多少，然后分别求出∠3、∠1、∠2的度数是多少，进而求出∠3+∠1﹣∠2的度数即可．

【解答】解：正三角形的每个内角是：

180°÷3=60°，

正方形的每个内角是：

360°÷4=90°，

正五边形的每个内角是：

（5﹣2）×180°÷5

=3×180°÷5

=540°÷5

=108°，

正六边形的每个内角是：

（6﹣2）×180°÷6

=4×180°÷6

=720°÷6

=120°，

则∠3+∠1﹣∠2

=（90°﹣60°）+﹣

=30°+12°﹣18°

=24°．

故答案为：24°．

第120题

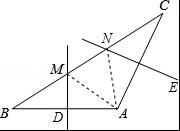
如图，在△ABC中，AB=AC，∠A=120°，BC=8cm，AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，则MN的长为　　．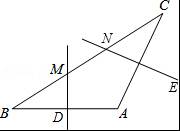

参考答案：8/3cm

解析：

【考点】线段垂直平分线的性质；等腰三角形的性质．

【分析】首先连接AM，AN，由在△ABC中，AB=AC，∠A=120°，可求得∠B=∠C=30°，又由AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，易得△AMN是等边三角形，继而求得答案．

【解答】解：连接AM，AN，

∵在△ABC中，AB=AC，∠A=120°，

∴∠C=∠B=30°，

∵AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，

∴AN=CN，AM=BM，

∴∠CAN=∠C=30°，∠BAM=∠B=30°，

∴∠ANC=∠AMN=60°，

∴△AMN是等边三角形，

∴AM=AN=MN，

∴BM=MN=CN，

∵BC=8cm，

∴MN=cm．

故答案为： cm．