八年级（上）期末数学试卷集（305题）

---

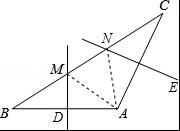
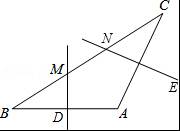
如图，在△ABC中，AB=AC，∠A=120°，BC=8cm，AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，则MN的长为　　．

知识点：试卷05

参考答案：8/3cm

解析：

【考点】线段垂直平分线的性质；等腰三角形的性质．

【分析】首先连接AM，AN，由在△ABC中，AB=AC，∠A=120°，可求得∠B=∠C=30°，又由AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，易得△AMN是等边三角形，继而求得答案．

【解答】解：连接AM，AN，

∵在△ABC中，AB=AC，∠A=120°，

∴∠C=∠B=30°，

∵AB的垂直平分线交BC于点M，交AB于点D，AC的垂直平分线交BC于点N，交AC于点E，

∴AN=CN，AM=BM，

∴∠CAN=∠C=30°，∠BAM=∠B=30°，

∴∠ANC=∠AMN=60°，

∴△AMN是等边三角形，

∴AM=AN=MN，

∴BM=MN=CN，

∵BC=8cm，

∴MN=cm．

故答案为： cm．