第181题

若x²+6x+k是完全平方式，则k=（　　）

A.9

B.﹣9

C.±9

D.±3

参考答案：A

解析：

【考点】完全平方式．

【专题】方程思想．

【分析】若x²+6x+k是完全平方式，则k是一次项系数6的一半的平方．

【解答】解：∵x²+6x+k是完全平方式，

∴（x+3）²=x²+6x+k，即x²+6x+9=x²+6x+k

∴k=9．

故选A．

【点评】本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．

第182题

把x³﹣2x²y+xy²分解因式，结果正确的是（　　）

A.x（x+y）（x﹣y）

B.x（x²﹣2xy+y²）

C.x（x+y）²

D.x（x﹣y）²

参考答案：D

解析：

【考点】提公因式法与公式法的综合运用．

【分析】此多项式有公因式，应先提取公因式，再对余下的多项式进行观察，有3项，可采用完全平方公式继续分解．

【解答】解：x³﹣2x²y+xy²，

=x（x²﹣2xy+y²），

=x（x﹣y）²．

故选D．

【点评】本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．

第183题

化简结果正确的是（　　）

A.ab

B.﹣ab

C.a²﹣b²

D.b²﹣a²

参考答案：B

解析：

【考点】约分．

【专题】计算题．

【分析】首先将分式的分子因式分解，进而约分求出即可．

【解答】解： ==﹣ab．

故选：B．

【点评】此题主要考查了约分，正确分解因式是解题关键．

第184题

解分式方程+=3时，去分母后变形为（　　）

A.2+（x+2）=3（x﹣1）

B.2﹣x+2=3（x﹣1）

C.2﹣（x+2）=3（1﹣x）

D.2﹣（x+2）=3（x﹣1）

参考答案：D

解析：

【考点】解分式方程．

【分析】本题考查对一个分式确定最简公分母，去分母得能力．观察式子x﹣1和1﹣x互为相反数，可得1﹣x=﹣（x﹣1），所以可得最简公分母为x﹣1，因为去分母时式子不能漏乘，所以方程中式子每一项都要乘最简公分母．

【解答】解：方程两边都乘以x﹣1，

得：2﹣（x+2）=3（x﹣1）．

故选D．

【点评】考查了解分式方程，对一个分式方程而言，确定最简公分母后要注意不要漏乘，这正是本题考查点所在．切忌避免出现去分母后：2﹣（x+2）=3形式的出现．

第185题

（3x+4y﹣6）²展开式的常数项是（　　）

A.﹣12

B.﹣6

C.9

D.36

参考答案：D

解析：

【考点】完全平方公式．

【分析】把3x+4y当作一个整体，根据完全平方公式展开，最后再根据完全平方公式和整式乘法法则展开，即可得出答案．

【解答】解：（3x+4y﹣6）²

=[（3x+4y）﹣6]²

=（3x+4y）²﹣2（3x+4y）•6+6²

=9x²+24xy+16y²﹣36x﹣48y+36，

常数项为36，

故选D．

【点评】本题考查了对完全平方公式的应用，能熟记完全平方公式的特点是解此题的关键，注意：完全平方公式有（a+b）²=a²+2ab+b²和（a﹣b）²=a²﹣2ab+b²．

第186题

如图，在△ABC中，点D在边BC上，若∠BAD=∠CAD，AB=6，AC=3，S_△ABD=3，则S_△ACD=（　　）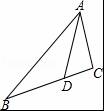

A.3

B.6

C.

D.

参考答案：C

解析：

【考点】角平分线的性质．

【分析】过D作DP⊥AC交AC的延长线于P，DQ⊥AB于Q，根据角平分线的性质得到DP=DQ，根据S_△ABD=AB•DQ=•DQ=3，求得DQ=1，得到DP=1，即可得到结论．

【解答】解：过D作DP⊥AC交AC的延长线于P，DQ⊥AB于Q，

∵∠BAD=∠CAD，

∴DP=DQ，

∵S_△ABD=AB•DQ=•DQ=3，

∴DQ=1，

∴DP=1，

∴S_△ACD=•AC•DP=，

故选：C．

【点评】本题考查了角平分线的性质，三角形的面积的计算，正确的作出辅助线是解题的关键．

第187题

如图，在等腰三角形纸片ABC中，AB=AC，∠A=40°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE的度数是（　　）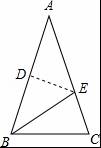

A.20°

B.30°

C.40°

D.70°

参考答案：B

解析：

【考点】翻折变换（折叠问题）；等腰三角形的性质．

【分析】如图，证明∠A=∠ABE=40°；证明∠ABC=∠C=70°，即可解决问题．

【解答】解：如图，由题意得：△ADE≌△BDE，

∴∠A=∠ABE=40°；

∵AB=AC，

∴∠ABC=∠C==70°，

∴∠CBE=30°，

故选B．

【点评】该题主要考查了翻折变换的性质、等腰三角形的性质、三角形的内角和定理及其应用问题；解题的关键是牢固掌握翻折变换的性质、等腰三角形的性质、三角形的内角和定理等知识点．

第188题

如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C、D为圆心，大于CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD．则下列说法错误的是（　　）

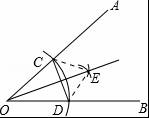
A.射线OE是∠AOB的平分线

B.△COD是等腰三角形

C.O、E两点关于CD所在直线对称

D.C、D两点关于OE所在直线对称

参考答案：C

解析：

【考点】作图—基本作图；轴对称的性质．

【分析】连接CE、DE，根据作图得到OC=OD、CE=DE，利用SSS证得△EOC≌△EOD从而证明得到射线OE平分∠AOB，判断A正确；

根据作图得到OC=OD，判断B正确；

根据作图不能得出CD平分OE，判断C错误；

根据作图得到OC=OD，由A得到射线OE平分∠AOB，根据等腰三角形三线合一的性质得到OE是CD的垂直平分线，判断D正确．

【解答】解：A、连接CE、DE，根据作图得到OC=OD、CE=DE．

∵在△EOC与△EOD中，

，

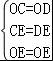∴△EOC≌△EOD（SSS），

∴∠AOE=∠BOE，即射线OE是∠AOB的平分线，正确，不符合题意；

B、根据作图得到OC=OD，

∴△COD是等腰三角形，正确，不符合题意；

C、根据作图不能得出CD平分OE，

∴CD不是OE的平分线，

∴O、E两点关于CD所在直线不对称，错误，符合题意；

D、根据作图得到OC=OD，

又∵射线OE平分∠AOB，

∴OE是CD的垂直平分线，

∴C、D两点关于OE所在直线对称，正确，不符合题意；

故选C．

【点评】本题考查了作图﹣基本作图，全等三角形的判定与性质，角平分线的性质，等腰三角形、轴对称的性质，从作图语句中提取正确信息是解题的关键．

第189题

在平面直角坐标中，已知点P（a，5）在第二象限，则点P关于直线m（直线m上各点的横坐标都是2）对称的点的坐标是（　　）

A.（﹣a，5）

B.（a，﹣5）

C.（﹣a+2，5）

D.（﹣a+4，5）

参考答案：D

解析：

【考点】坐标与图形变化-对称．

【分析】利用已知直线m上各点的横坐标都是2，得出其解析式，再利用对称点的性质得出答案．

【解答】解：∵直线m上各点的横坐标都是2，

∴直线为：x=2，

∵点P（a，5）在第二象限，

∴a到2的距离为：2﹣a，

∴点P关于直线m对称的点的横坐标是：2﹣a+2=4﹣a，

故P点对称的点的坐标是：（﹣a+4，5）．

故选：D．

【点评】此题主要考查了坐标与图形的性质，根据题意得出对称点的横坐标是解题关键．

第190题

将边长分别为a+b和a﹣b的两个正方形摆放成如图所示的位置，则阴影部分的面积化简后的结果是（　　）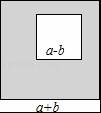

A.a﹣b

B.a+b

C.2ab

D.4ab

参考答案：D

解析：

【考点】整式的混合运算．

【分析】根据图形得出阴影部分的面积为（a+b）²﹣（a﹣b）²，再求出即可．

【解答】解：阴影部分的面积为（a+b）²﹣（a﹣b）²

=a²+2ab+b²﹣（a²﹣2ab+b²）

=4ab，

故选D．

【点评】本题考查了整式的混合运算的应用，能正确根据题意列出算式是解此题的关键在，注意运算顺序．

第191题

25的算术平方根是　　．

参考答案：5

解析：

【考点】算术平方根．

【分析】根据算术平方根的定义即可求出结果，算术平方根只有一个正根．

【解答】解：∵5²=25，

∴25的算术平方根是5．

故答案为：5．

【点评】易错点：算术平方根的概念易与平方根的概念混淆而导致错误．规律总结：弄清概念是解决本题的关键．

第192题

若分式的值为0，则x=　　．

参考答案：1

解析：

【考点】分式的值为零的条件．

【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0．两个条件需同时具备，缺一不可．据此可以解答本题．

【解答】解：分式的值为0，得

x²﹣1=0且x+1≠0．解得x=1，

故答案为：1．

【点评】此题主要考查了分式值为零的条件，关键是掌握分式值为零的条件是分子等于零且分母不等于零．注意：“分母不为零”这个条件不能少．

第193题

如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=2，则EF=　　．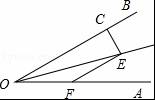

参考答案：4

解析：

【考点】含30度角的直角三角形；角平分线的性质．

【分析】作EG⊥OA于F，根据角平分线的性质得到EG的长度，再根据平行线的性质得到∠OEF=∠COE=15°，然后利用三角形的外角和内角的关系求出∠EFG=30°，利用30°角所对的直角边是斜边的一半解题．

【解答】解：作EG⊥OA于G，如图所示：

∵EF∥OB，∠AOE=∠BOE=15°

∴∠OEF=∠COE=15°，EG=CE=2，

∵∠AOE=15°，

∴∠EFG=15°+15°=30°，

∴EF=2EG=4．

故答案为：4．

【点评】本题考查了角平分线的性质、平行线的性质、含30°角的直角三角形的性质；熟练掌握角平分线的性质，证出∠EFG=30°是解决问题的关键．

第194题

一艘轮船在静水中的速度为a千米/时，若A、B两个港口之间的距离为50千米，水流的速度为b千米/时，轮船往返两个港口之间一次需　　小时．

参考答案：

解析：

【考点】列代数式（分式）．

【专题】推理填空题．

【分析】根据一艘轮船在静水中的速度为a千米/时，若A、B两个港口之间的距离为50千米，水流的速度为b千米/时，可以得到轮船往返两个港口之间一次需要的时间．

【解答】解：由题意可得，假设A到B顺流，则B到A逆流，

轮船往返两个港口之间需要的时间为： =小时，

故答案为：．

【点评】本题考查列代数式，解题的关键是明确题意，列出相应的代数式．

第195题

计算：（2x+1）（x+3）．

参考答案：见解析

解析：

【考点】多项式乘多项式．

【分析】直接利用多项式乘以多项式运算法则进而得出答案．

【解答】解：（2x+1）（x+3）

=2x²+6x+x+3

=2x²+7x+3．

【点评】此题主要考查了多项式乘以多项式，正确掌握运算法则是解题关键．

第196题

计算：（ +﹣）÷．

参考答案：见解析

解析：

【考点】二次根式的混合运算．

【专题】计算题．

【分析】先把二次根式化为最简二次根式，然后合并后进行二次根式的除法运算．

【解答】解：原式=（4+3﹣2）÷

=5÷

=．

【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．

第197题

解方程： +1=．

参考答案：见解析

解析：

【考点】解分式方程．

【专题】计算题．

【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

【解答】解：去分母得：4x+2x+6=7，

移项合并得：6x=1，

解得：x=，

经检验，x=是分式方程的解．

【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

第198题

先化简，再求值：÷（x+3﹣），其中x=3．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】先化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．

【解答】解：÷（x+3﹣）

=

=

=，

当x=3时，原式=．

【点评】本题考查分式的化简求值，解题的关键是明确分式化简求值的方法．

第199题

已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

（1）∠AEC=∠BED；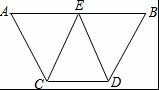

参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【专题】证明题．

【分析】（1）根据CE=DE得出∠ECD=∠EDC，再利用平行线的性质进行证明即可；

（2）根据SAS证明△AEC与△BED全等，再利用全等三角形的性质证明即可．

【解答】证明：（1）∵AB∥CD，

∴∠AEC=∠ECD，∠BED=∠EDC，

∵CE=DE，

∴∠ECD=∠EDC，

∴∠AEC=∠BED；

（2）∵E是AB的中点，

∴AE=BE，

在△AEC和△BED中，

，

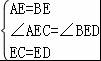∴△AEC≌△BED（SAS），

∴AC=BD．

【点评】本题主要考查了全等三角形的判定以及全等三角形的性质，关键是根据SAS证明全等．

第200题

如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD．

求证：CE=BD．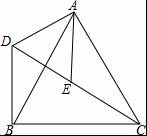

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等边三角形的性质．

【分析】由等边三角形的性质就可以得出AD=AE，AB=AC，∠DAE=∠BAC=60°，由等式的性质就可以得出∠DAB=∠EAC，就可以得出△ADB≌△AEC而得出结论．

【解答】解：∵△ACB和△ADE均为等边三角形，

∴AD=AE，AB=AC，∠DAE=∠BAC=60°，

∴∠DAE﹣∠BAE=∠BAC﹣∠BAE，

∴∠DAB=∠EAC．

在△ADB和△AEC中，

，

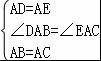∴△ADB≌△AEC（SAS），

∴CE=BD．

【点评】本题考查了等边三角形的性质的运用，等式的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．