第221题

（1）分解因式：（p﹣4）（p+1）+3p；

（2）计算：8（x+2）²﹣（3x﹣1）（3x+1）．

参考答案：见解析

解析：

【考点】整式的混合运算．

【分析】（1）原式整理后，利用平方差公式分解即可；

（2）原式利用平方差公式及完全平方公式化简即可得到结果．

【解答】解：（1）原式=p²﹣3p﹣4+3p=p²﹣4=（p+2）（p﹣2）；

（2）原式=8x²+32x+32﹣9x²+1=﹣x²+32x+33．

第222题

设A=，B=+1，当x为何值时，A与B的值相等．

参考答案：见解析

解析：

【考点】解分式方程．

【分析】A与B的值相等，让两个代数式相等，化为分式方程求解．

【解答】解：当A=B时， =+1，

=+1，

方程两边同时乘以（x+1）（x﹣1），

得x（x+1）=3+（x+1）（x﹣1），

x+x=3+x﹣1，

∴x=2．

检验，当x=2时，（x+1）（x﹣1）=3≠0．

∴x=2是分式方程的根．

因此，当x=2时，A=B．

第223题

先化简（1﹣）÷，再从0，﹣2，﹣1，1中选择一个合适的数代入并求值．

参考答案：见解析

解析：

【考点】分式的化简求值．

【分析】先把分式的分子和分母因式分解，并且把除法运算转化为乘法运算得到原式=•，约分后得到原式=，由于x不能取±1，2，所以可以把x=0代入计算．

【解答】解：原式=•

=，

当x=0时，原式==﹣．

第224题

如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕．

（1）试判断B′E与DC的位置关系；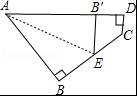

参考答案：见解析

解析：

【考点】全等三角形的判定与性质．

【分析】（1）由于AB′是AB的折叠后形成的，所以∠AB′E=∠B=∠D=90°，∴B′E∥DC；

（2）利用平行线的性质和全等三角形求解．

【解答】解：（1）由于AB′是AB的折叠后形成的，

∠AB′E=∠B=∠D=90°，

∴B′E∥DC；

（2）∵折叠，

∴△ABE≌△AB′E，

∴∠AEB′=∠AEB，即∠AEB=∠BEB′，

∵B′E∥DC，∴∠BEB′=∠C=130°，

∴∠AEB=∠BEB′=65°．

第225题

如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．

（1）求证：△AOB≌△DOC；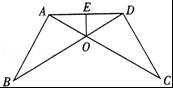

参考答案：见解析

解析：

【考点】全等三角形的判定．

【分析】（1）由已知可以利用AAS来判定其全等；

（2）再根据等腰三角形三线合一的性质即可求得其为直角．

【解答】（1）证明：在△AOB和△DOC中

∵

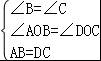
∴△AOB≌△DOC（AAS）

（2）解：∵△AOB≌△DOC，

∴AO=DO

∵E是AD的中点

∴OE⊥AD

∴∠AEO=90°

第226题

某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．

（1）该商家购进的第一批衬衫是多少件？

参考答案：见解析

解析：

【考点】分式方程的应用；一元一次不等式的应用．

【分析】（1）可设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，根据第二批这种衬衫单价贵了10元，列出方程求解即可；

（2）设每件衬衫的标价y元，求出利润表达式，然后列不等式解答．

【解答】解：（1）设该商家购进的第一批衬衫是x件，则购进第二批这种衬衫是2x件，依题意有

+10=，

解得x=120，

经检验，x=120是原方程的解，且符合题意．

答：该商家购进的第一批衬衫是120件．

（2）3x=3×120=360，

设每件衬衫的标价y元，依题意有

y+50×0.8y≥×（1+25%），

解得y≥150．

答：每件衬衫的标价至少是150元．

第227题

已知：如图，△ABC为等边三角形，过AB边上的点D作DG∥BC，交AC于G，在GD的延长线上取点E，使DE=DB，连接AE，CD．

（1）求证：△AGE≌△DAC；

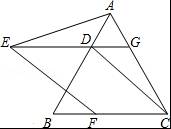
参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等边三角形的性质；平移的性质．

【分析】（1）根据已知等边三角形的性质可推出△ADG是等边三角形，从而再利用SAS判定△AGE≌△DAC；

（2）连接AF，由已知可得四边形EFCD是平行四边形，从而得到EF=CD，∠DEF=∠DCF，由（1）知△AGE≌△DAC得到AE=CD，∠AED=∠ACD，从而可得到EF=AE，∠AEF=60°，所以△AEF为等边三角形．

【解答】（1）证明：∵△ABC是等边三角形，

∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°．

∵EG∥BC，

∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°．

∴△ADG是等边三角形．

∴AD=DG=AG．

∵DE=DB，

∴EG=AB．

∴GE=AC．

∵EG=AB=CA，

∴∠AGE=∠DAC=60°，

在△AGE和△DAC中，

，

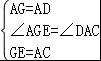∴△AGE≌△DAC（SAS）．

（2）解：△AEF为等边三角形．

证明：如图，连接AF，

∵DG∥BC，EF∥DC，

∴四边形EFCD是平行四边形，

∴EF=CD，∠DEF=∠DCF，

由（1）知△AGE≌△DAC，

∴AE=CD，∠AED=∠ACD．

∵EF=CD=AE，∠AED+∠DEF=∠ACD+∠DCB=60°，

∴△AEF为等边三角形．

第228题

下列大学的校徽图案中，是轴对称图形的是（　　）

A.

B.

C.

D.

参考答案：C

解析：

【考点】轴对称图形．

【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行解答即可．

【解答】解：A、不是轴对称图形，故此选项错误；

B、不是轴对称图形，故此选项错误；

C、是轴对称图形，故此选项正确；

D、不是轴对称图形，故此选项错误；

故选：C．

【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．

第229题

下列运算正确的是（　　）

A.3x²+2x³=5x⁵

B.（π﹣3.14）⁰=0

C.3^﹣2=﹣6

D.（x³）²=x⁶

参考答案：D

解析：

【考点】幂的乘方与积的乘方；合并同类项；零指数幂；负整数指数幂．

【分析】根据合并同类项法则、零指数幂、负整数指数幂、幂的乘方分别求出每个式子的值，再判断即可．

【解答】解：A、3x²和2x³不能合并，故本选项错误；

B、结果是1，故本选项错误；

C、结果是，故本选项错误；

D、结果是x⁶，故本选项正确；

故选D．

【点评】本题考查了合并同类项法则、零指数幂、负整数指数幂、幂的乘方的应用，能求出每个式子的值是解此题的关键．

第230题

若分式有意义，则x的取值范围是（　　）

A.x≠3

B.x≠﹣3

C.x＞3

D.x＞﹣3

参考答案：B

解析：

【考点】分式有意义的条件．

【分析】根据分式有意义的条件可得x+3≠0，再解即可．

【解答】解：由题意得：x+3≠0，

解得：x≠3，

故选：B．

【点评】此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．

第231题

若x²﹣kxy+9y²是一个完全平方式，则k的值为（　　）

A.3

B.±6

C.6

D.+3

参考答案：B

解析：

【考点】完全平方式．

【分析】根据首末两项是x和3y的平方，那么中间项为加上或减去x和3y的乘积的2倍，进而得出答案．

【解答】解：∵x²﹣kxy+9y²是完全平方式，

∴﹣kxy=±2×3y•x，

解得k=±6．

故选：B．

【点评】本题主要考查了完全平方公式，根据两平方项确定出这两个数，再根据乘积二倍项求解是解题关键．

第232题

下列长度的三条线段，能组成三角形的是（　　）

A.3，4，8

B.5，6，11

C.12，5，6

D.3，4，5

参考答案：D

解析：

【考点】三角形三边关系．

【分析】根据三角形的三边关系进行分析判断，两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．

【解答】解：根据三角形任意两边的和大于第三边，

A选项中，3+4=7＜8，不能组成三角形；

B选项中，5+6=11，不能组成三角形；

C选项中，5+6=11＜12，不能够组成三角形；

D选项中，3+4＞5，能组成三角形．

故选D．

【点评】本题考查了能够组成三角形三边的条件：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．

第233题

如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是（　　）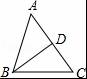

A.85°

B.80°

C.75°

D.70°

参考答案：A

解析：

【考点】三角形内角和定理．

【分析】先根据∠A=50°，∠ABC=70°得出∠C的度数，再由BD平分∠ABC求出∠ABD的度数，再根据三角形的外角等于和它不相邻的内角的和解答．

【解答】解：∵∠ABC=70°，BD平分∠ABC，

∴∠ABD=70°×=35°，

∴∠BDC=50°+35°=85°，

故选：A．

【点评】本题考查的是三角形的外角和内角的关系，熟知三角形的外角等于和它不相邻的内角的和是解题的关键．

第234题

如图，AB=AD，要说明△ABC≌△ADE，需添加的条件不能是（　　）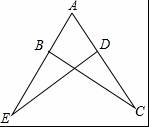

A.∠E=∠C

B.AC=AE

C.∠ADE=∠ABC

D.DE=BC

参考答案：D

解析：

【考点】全等三角形的判定．

【分析】由条件AB=AD，结合∠A=∠A，要使△ABC≌△ADE则需添加一组角相等或AC=AE，则可求得答案．

【解答】解：

∵AB=AD，且∠A=∠A，

∴当∠E=∠C时，满足AAS，可证明△ABC≌△ADE，

当AC=AE时，满足SAS，可证明△ABC≌△ADE，

当∠ADE=∠ABC时，满足ASA，可证明△ABC≌△ADE，

当DE=BC时，满足SSA，不能证明△ABC≌△ADE，

故选D．

【点评】本题主要考查全等三角形的判定，掌握全等三角形的判定方法是解题的关键，即SSS、SAS、ASA、AAS和HL．

第235题

已知﹣=，则的值为（　　）

A.

B.

C.﹣2

D.2

参考答案：C

解析：

【考点】分式的加减法．

【专题】计算题；分式．

【分析】已知等式通分并利用同分母分式的减法法则计算，整理即可求出所求式子的值．

【解答】解：已知等式整理得： =，即=﹣，

则原式=﹣2，

故选C

【点评】此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

第236题

若分式方程无解，则m的值为（　　）

A.﹣1

B.0

C.1

D.3

参考答案：A

解析：

【考点】分式方程的解．

【专题】计算题；分式方程及应用．

【分析】分式方程去分母转化为整式方程，由分式方程无解求出x的值，代入整式方程计算即可求出m的值．

【解答】解：去分母得：x+2=m，

由分式方程无解得到x=﹣3，

代入整式方程得：m=﹣1，

故选A

【点评】此题考查了分式方程的解，分式方程无解即为最简公分母为0．

第237题

如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF，CE、下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（　　）

A.1个

B.2个

C.3个

D.4个

参考答案：D

解析：

【考点】全等三角形的判定与性质．

【分析】根据题意，结合已知条件与全等的判定方法对选项一一进行分析论证，排除错误答案．

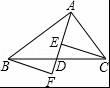
【解答】解：∵AD是△ABC的中线，

∴BD=CD，又∠CDE=∠BDF，DE=DF，

∴△BDF≌△CDE，故④正确；

由△BDF≌△CDE，可知CE=BF，故①正确；

∵AD是△ABC的中线，

∴△ABD和△ACD等底等高，

∴△ABD和△ACD面积相等，故②正确；

由△BDF≌△CDE，可知∠FBD=∠ECD

∴BF∥CE，故③正确．

故选：D．

【点评】本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

第238题

计算：﹣|﹣5|+（2016﹣π）⁰﹣（）^﹣2=　　．

参考答案：﹣11

解析：

【考点】实数的运算；零指数幂；负整数指数幂．

【专题】计算题；实数．

【分析】原式利用平方根定义，绝对值的代数意义，零指数幂、负整数指数幂法则计算即可得到结果．

【解答】解：原式=2﹣5+1﹣9=﹣11，

故答案为：﹣11

【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

第239题

若分式的值为0，则x=　　．

参考答案：2

解析：

【考点】分式的值为零的条件．

【专题】计算题．

【分析】分式的值是0的条件是，分子为0，分母不为0．

【解答】解：∵x²﹣4=0，

∴x=±2，

当x=2时，x+2≠0，

当x=﹣2时，x+2=0．

∴当x=2时，分式的值是0．

故答案为：2．

【点评】分式是0的条件中特别需要注意的是分母不能是0，这是经常考查的知识点．

第240题

已知2^x=3，则2^x+3的值为　　．

参考答案：24

解析：

【考点】同底数幂的乘法．

【分析】根据同底数幂的乘法，可得答案．

【解答】解：2^x+3=2^x×2³=3×8=24，

故答案为：24．

【点评】本题考察了同底数幂的乘法，熟记法则并根据法则计算是解题关键．